12 15 As A Percent
saludintensiva
Sep 18, 2025 · 5 min read
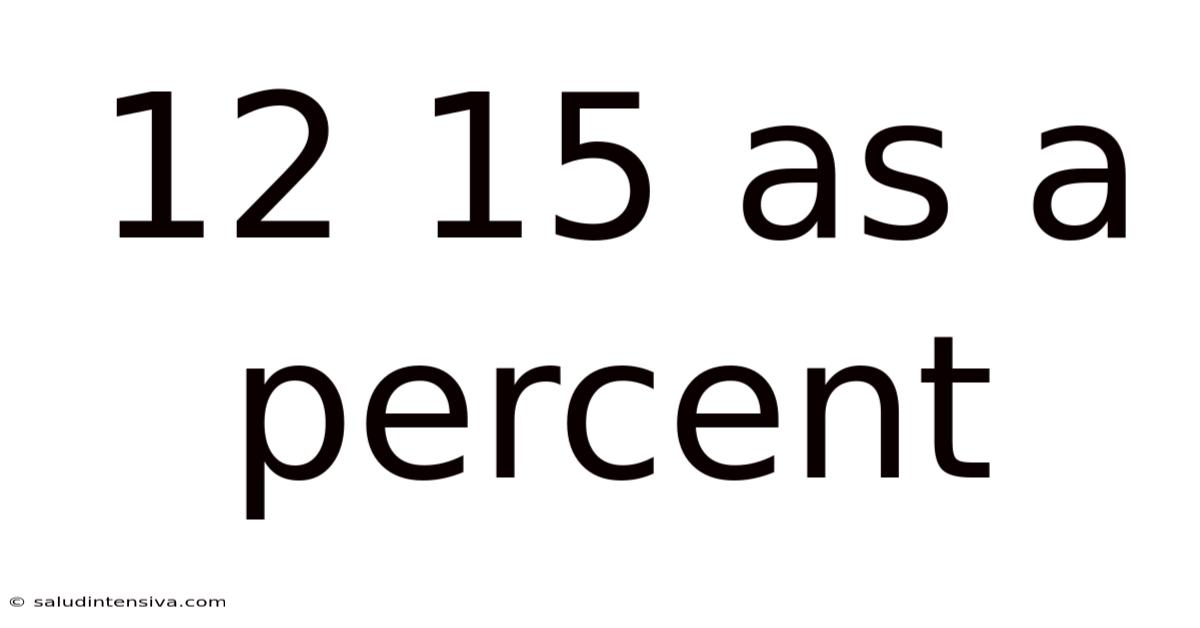
Table of Contents
Understanding 12/15 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and interest rates to understanding statistics and data analysis. This article will delve into the process of converting the fraction 12/15 into a percentage, explaining the steps involved, providing a deeper understanding of the underlying principles, and exploring related concepts. We'll also address frequently asked questions to ensure a comprehensive understanding of this topic.
Understanding Fractions and Percentages
Before we jump into converting 12/15, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates the total number of equal parts the whole is divided into.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred." Therefore, 50% means 50 out of 100, or 50/100. Percentages are incredibly useful because they allow for easy comparison of proportions across different quantities.
Method 1: Simplifying the Fraction
The first step in converting 12/15 to a percentage is to simplify the fraction. Simplifying a fraction means finding an equivalent fraction with a smaller numerator and denominator. We do this by finding the greatest common divisor (GCD) of the numerator and denominator.
The GCD of 12 and 15 is 3. Dividing both the numerator and denominator by 3, we get:
12 ÷ 3 = 4 15 ÷ 3 = 5
So, 12/15 simplifies to 4/5. This simplified fraction is equivalent to the original fraction, meaning it represents the same proportion.
Method 2: Converting the Simplified Fraction to a Decimal
Now that we have the simplified fraction 4/5, we can convert it to a decimal. To do this, we divide the numerator by the denominator:
4 ÷ 5 = 0.8
Therefore, 4/5 is equal to 0.8.
Method 3: Converting the Decimal to a Percentage
The final step is to convert the decimal 0.8 to a percentage. To do this, we multiply the decimal by 100 and add the "%" symbol:
0.8 x 100 = 80
Therefore, 0.8 is equal to 80%.
Conclusion: Following these steps, we find that 12/15 is equivalent to 80%.
Alternative Method: Direct Conversion
Alternatively, you can directly convert the fraction 12/15 to a percentage without simplifying first. This involves dividing the numerator by the denominator and multiplying the result by 100:
(12 ÷ 15) x 100 = 0.8 x 100 = 80%
This method yields the same result, demonstrating that simplifying the fraction is an optional step, although it often simplifies the calculations.
Real-World Applications of Percentage Conversions
The ability to convert fractions to percentages is crucial in many real-world scenarios. Consider these examples:
- Discounts: A store offers a 20% discount on an item. If the original price is $50, the discount amount is (20/100) x $50 = $10. Understanding percentages helps calculate the final price after the discount.
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding percentage calculations is crucial for managing personal finances effectively.
- Test Scores: Test scores are often expressed as percentages. A score of 85% indicates that 85 out of 100 possible points were earned.
- Surveys and Polls: Survey results and poll data are frequently represented as percentages to show the proportion of respondents who chose a particular option.
- Data Analysis: In various fields, data is analyzed and presented using percentages to highlight trends, patterns, and comparisons.
Understanding the Concept of Proportionality
The conversion from fractions to percentages highlights the concept of proportionality. The fraction 12/15, the simplified fraction 4/5, the decimal 0.8, and the percentage 80% all represent the same proportion – four parts out of five, or 80 parts out of 100. Understanding this underlying proportionality is vital for grasping the meaning of percentages and their applications.
Further Exploration: Working with More Complex Fractions
While this article focused on 12/15, the same principles apply to converting any fraction to a percentage. For example, let's consider the fraction 7/8:
- Divide the numerator by the denominator: 7 ÷ 8 = 0.875
- Multiply by 100 to convert to a percentage: 0.875 x 100 = 87.5%
Therefore, 7/8 is equal to 87.5%. This illustrates the general method for converting any fraction to a percentage, regardless of its complexity.
Frequently Asked Questions (FAQ)
Q1: What if the fraction results in a repeating decimal?
A1: Some fractions, when converted to decimals, result in repeating decimals (e.g., 1/3 = 0.333...). In such cases, you can either round the decimal to a certain number of decimal places before converting to a percentage or express the percentage using the repeating decimal (e.g., 33.333...). The level of precision depends on the context of the problem.
Q2: Can I convert a mixed number to a percentage?
A2: Yes! First, convert the mixed number into an improper fraction. For example, let's consider the mixed number 2 1/2. Convert it to an improper fraction: (2 x 2) + 1 = 5/2. Then, follow the steps outlined above to convert the improper fraction to a percentage: (5 ÷ 2) x 100 = 250%.
Q3: Why is understanding percentage conversion important?
A3: Percentage conversion is vital for everyday life and many professional fields. It allows for easy comparison of proportions, making it crucial in areas like finance, statistics, data analysis, and more.
Q4: Are there any online calculators for percentage conversion?
A4: While this article focuses on understanding the underlying principles, many online calculators can perform percentage conversions quickly and accurately. However, grasping the mathematical concepts will enable you to perform these calculations independently and understand the results more thoroughly.
Conclusion: Mastering Percentage Conversions
Converting fractions like 12/15 to percentages is a straightforward process involving simple steps: simplifying the fraction (if possible), converting the fraction to a decimal, and then multiplying by 100 to obtain the percentage. This skill is invaluable in numerous practical applications, demonstrating the importance of understanding this fundamental mathematical concept. Through consistent practice and a deeper understanding of the underlying principles, you can build confidence in your ability to handle percentage conversions efficiently and accurately. The ability to confidently work with percentages unlocks a wider understanding of numerical relationships and their applications in the world around us.
Latest Posts
Latest Posts
-
Lb Ft2 To Kg M2
Sep 18, 2025
-
What Is Equal To 9 12
Sep 18, 2025
-
47 50 As A Decimal
Sep 18, 2025
-
1470 Sq Ftt To Acres
Sep 18, 2025
-
14 Percent In Decimal Form
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 12 15 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.