What Is Equal To 9/12
saludintensiva
Sep 18, 2025 · 5 min read
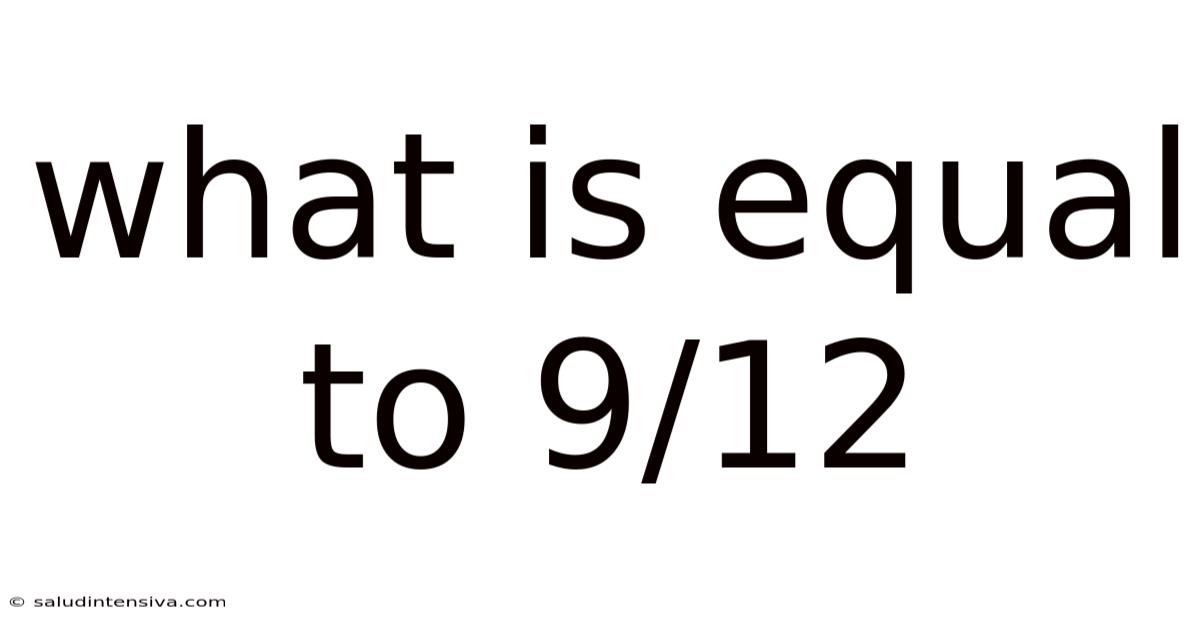
Table of Contents
What is Equal to 9/12? A Deep Dive into Fractions, Simplification, and Equivalent Fractions
Understanding fractions is fundamental to mathematics, and the question "What is equal to 9/12?" opens the door to exploring several key concepts. This article will not only answer that question directly but also delve into the underlying principles of fraction simplification, equivalent fractions, and their applications in various fields. We'll explore different methods for solving this problem and provide a comprehensive understanding for learners of all levels.
Understanding Fractions: A Quick Refresher
Before we tackle 9/12, let's revisit the basics of fractions. A fraction represents a part of a whole. It's written as a/b, where:
- 'a' is the numerator: This represents the number of parts you have.
- 'b' is the denominator: This represents the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) indicates you have 3 parts, and the denominator (4) indicates the whole is divided into 4 equal parts.
Finding the Equivalent Fraction: Simplifying 9/12
The fraction 9/12 represents 9 out of 12 equal parts. To find what's equal to 9/12, we need to simplify it to its simplest form. This involves finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Finding the GCD:
There are several ways to find the GCD of 9 and 12:
-
Listing Factors: List the factors of each number and find the largest one they share.
- Factors of 9: 1, 3, 9
- Factors of 12: 1, 2, 3, 4, 6, 12
- The largest common factor is 3.
-
Prime Factorization: Break down each number into its prime factors. The GCD is the product of the common prime factors raised to the lowest power.
- 9 = 3 x 3 = 3²
- 12 = 2 x 2 x 3 = 2² x 3
- The common prime factor is 3, and its lowest power is 3¹. Therefore, the GCD is 3.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
- 12 ÷ 9 = 1 with a remainder of 3
- 9 ÷ 3 = 3 with a remainder of 0 The GCD is 3.
Simplifying the Fraction:
Once we have the GCD (which is 3), we divide both the numerator and the denominator by it:
9 ÷ 3 = 3 12 ÷ 3 = 4
Therefore, the simplified fraction is 3/4. This means 9/12 is equal to 3/4.
Understanding Equivalent Fractions
Equivalent fractions are fractions that represent the same value, even though they look different. We can obtain equivalent fractions by multiplying or dividing both the numerator and denominator by the same non-zero number.
For example:
- Multiplying: If we multiply both the numerator and denominator of 3/4 by 2, we get 6/8, which is equivalent to 3/4.
- Dividing: If we divide both the numerator and denominator of 6/8 by 2, we get 3/4.
This principle demonstrates that there are infinitely many fractions equivalent to 3/4 (and therefore to 9/12). However, 3/4 is the simplest form because it cannot be further simplified.
Visual Representation of Equivalent Fractions
Imagine a pizza cut into 12 slices. If you eat 9 slices, you've eaten 9/12 of the pizza. Now, imagine the same pizza cut into only 4 slices. Eating 3 out of these 4 slices represents the same amount of pizza (3/4). This visual representation helps solidify the concept of equivalent fractions.
Applications of Fractions and Simplification
The ability to simplify fractions is crucial in various fields:
- Mathematics: Simplifying fractions is essential for solving equations, performing calculations, and understanding relationships between quantities.
- Science: Fractions are used extensively in scientific measurements, data analysis, and expressing ratios and proportions.
- Engineering: Engineers use fractions in calculations related to dimensions, materials, and structural designs.
- Cooking and Baking: Recipes often involve fractions for precise measurements of ingredients.
- Everyday Life: We encounter fractions daily, from dividing a pizza to understanding discounts and percentages.
Frequently Asked Questions (FAQ)
Q1: Is there only one fraction equal to 9/12?
A1: No, there are infinitely many fractions equal to 9/12 (or 3/4). Any fraction obtained by multiplying or dividing both the numerator and denominator of 3/4 by the same non-zero number will be equivalent.
Q2: Why is simplifying fractions important?
A2: Simplifying fractions makes calculations easier and allows for clearer understanding. It helps in comparing fractions and expressing results in a concise and efficient manner.
Q3: What if I don't find the GCD immediately?
A3: Don't worry! You can simplify a fraction in multiple steps. If you don't find the GCD right away, just divide the numerator and denominator by any common factor. Repeat this process until you reach the simplest form. For example, you could divide 9/12 by 3 to get 3/4 in one step. Alternatively, you could divide by 3 first to get 3/4, then find that you cannot simplify any further.
Q4: How can I check if two fractions are equivalent?
A4: To check if two fractions are equivalent, cross-multiply. If the products are equal, the fractions are equivalent. For example, to check if 9/12 and 3/4 are equivalent:
- 9 x 4 = 36
- 12 x 3 = 36 Since the products are equal, the fractions are equivalent.
Conclusion: Mastering Fractions for a Brighter Future
The simple question, "What is equal to 9/12?", has led us on a journey through the fascinating world of fractions. We've learned how to simplify fractions, understand equivalent fractions, and appreciate their wide-ranging applications. Mastering these concepts is not just about solving mathematical problems; it's about developing a deeper understanding of numerical relationships and their practical relevance in various aspects of life. Continue to practice and explore the world of fractions, and you'll find yourself better equipped to tackle more complex mathematical challenges and real-world situations. Remember, the key to mastering fractions lies in understanding the underlying principles and practicing regularly.
Latest Posts
Latest Posts
-
List The Multiples Of 3
Sep 18, 2025
-
4 25 As A Percent
Sep 18, 2025
-
Odds Of Winning Raffle Calculator
Sep 18, 2025
-
4 13 As A Percent
Sep 18, 2025
-
Round To The Nearest Year
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is Equal To 9/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.