4 25 As A Percent
saludintensiva
Sep 18, 2025 · 6 min read
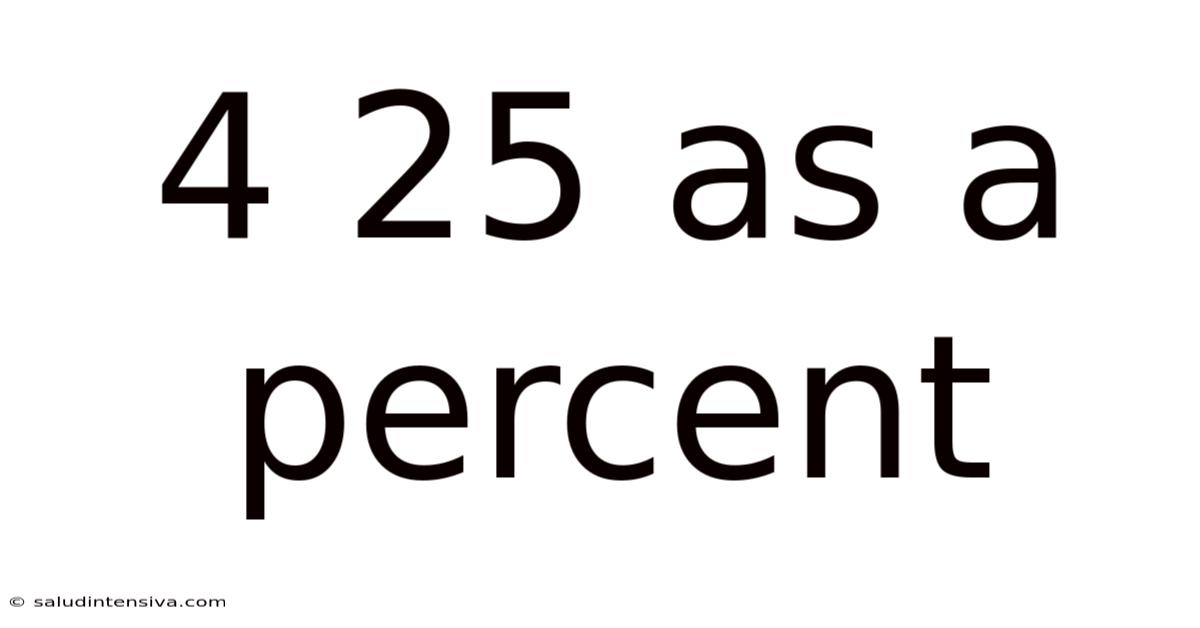
Table of Contents
Decoding 4/25 as a Percentage: A Comprehensive Guide
Understanding fractions and percentages is fundamental to various aspects of life, from calculating discounts in a shop to comprehending financial reports. This comprehensive guide delves into the conversion of the fraction 4/25 into a percentage, explaining the process in detail and exploring related concepts. We’ll move beyond the simple conversion, examining the underlying mathematical principles and providing practical examples to solidify your understanding. This will not only answer "What is 4/25 as a percent?" but also equip you with the tools to tackle similar problems independently.
Understanding Fractions and Percentages
Before we dive into the specific conversion of 4/25, let's establish a solid understanding of the basic concepts. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole.
A percentage, on the other hand, represents a fraction of 100. It expresses a proportion out of 100, denoted by the symbol "%". For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are widely used because they provide a standardized way to compare different proportions.
Converting Fractions to Percentages: The Step-by-Step Process
Converting a fraction to a percentage involves two main steps:
-
Convert the fraction to a decimal: This involves dividing the numerator by the denominator.
-
Convert the decimal to a percentage: This is done by multiplying the decimal by 100 and adding the "%" symbol.
Let's apply this process to our fraction, 4/25:
Step 1: Convert 4/25 to a decimal
4 ÷ 25 = 0.16
Step 2: Convert the decimal 0.16 to a percentage
0.16 x 100 = 16%
Therefore, 4/25 is equal to 16%.
Alternative Methods for Conversion
While the above method is straightforward, there are alternative approaches you can use, particularly helpful when dealing with fractions that aren't easily divisible:
- Finding an Equivalent Fraction with a Denominator of 100: If you can easily find an equivalent fraction with a denominator of 100, the conversion to a percentage becomes much simpler. In this case, we can multiply both the numerator and the denominator of 4/25 by 4:
(4 x 4) / (25 x 4) = 16/100
Since 16/100 represents 16 out of 100, the percentage is directly 16%. This method highlights the core concept of percentages as proportions out of 100.
- Using Proportions: You can set up a proportion to solve for the percentage. Let 'x' represent the percentage:
4/25 = x/100
Cross-multiplying gives:
25x = 400
Solving for x:
x = 400/25 = 16
Therefore, x = 16%, confirming our previous result. This method reinforces the proportional relationship between fractions and percentages.
Practical Applications of 4/25 as a Percentage
Understanding that 4/25 equals 16% has several practical applications:
-
Sales and Discounts: Imagine a store offering a 16% discount on an item. If the original price was $100, the discount would be 16% of $100, which is $16. This means the final price would be $84. This demonstrates the direct application of percentages in calculating discounts.
-
Financial Calculations: In finance, percentages are crucial for understanding interest rates, profit margins, and returns on investments. Knowing that 4/25 represents 16% allows for quick calculations in these scenarios. For example, a 16% annual interest on a $500 investment would yield $80 in interest at the end of the year.
-
Data Analysis and Statistics: Percentages are frequently used to represent proportions in data analysis and statistics. For instance, if a survey shows that 4 out of 25 respondents prefer a certain product, it means 16% of the respondents prefer that product. This shows how percentages help present data concisely and understandably.
-
Everyday Life: Percentages appear in various everyday contexts, from calculating tips in restaurants (a 16% tip on a $50 bill would be $8) to understanding nutritional information on food labels (16% of daily recommended value of a nutrient). These examples demonstrate the pervasive nature of percentage application in our daily life.
Understanding the Mathematical Principles
The conversion from fraction to percentage relies on the fundamental concept of equivalent fractions and the definition of a percentage as a fraction with a denominator of 100. The division in the first step of the conversion process effectively transforms the fraction into its decimal representation. Multiplying by 100 in the second step scales this decimal representation to express the fraction as a proportion out of 100, which is the essence of a percentage.
The alternative method using equivalent fractions directly shows how to manipulate the fraction to get a denominator of 100, making the percentage immediately apparent. The proportion method utilizes the proportional relationship between the fraction and its percentage equivalent, providing an algebraic approach to solve for the unknown percentage. Understanding these underlying principles allows for a deeper comprehension of the conversion process and enables problem-solving flexibility.
Frequently Asked Questions (FAQ)
-
Q: Can I convert any fraction to a percentage?
A: Yes, absolutely. Any fraction can be converted to a percentage using the methods described above.
-
Q: What if the fraction results in a repeating decimal?
A: If the division results in a repeating decimal, you can round the decimal to a certain number of decimal places before converting to a percentage. For example, if you get 0.3333..., you might round it to 0.33 and convert it to 33%.
-
Q: Are there any online calculators to help with these conversions?
A: While this article focuses on the process, yes, many online calculators are available to perform these conversions quickly. However, understanding the underlying principles is crucial for problem-solving abilities and deeper understanding.
-
Q: Why are percentages so commonly used?
A: Percentages provide a standardized and easily understandable way to compare proportions. They're universally understood, making them a practical tool for communication and analysis across various fields.
-
Q: How can I improve my understanding of fractions and percentages?
A: Practice is key. Work through various examples, try different conversion methods, and apply your knowledge to real-world problems. Consider exploring online resources and educational materials to further deepen your understanding.
Conclusion
Converting 4/25 to a percentage is a straightforward process that involves converting the fraction to a decimal and then multiplying by 100. The result, 16%, represents 16 parts out of 100. Understanding this conversion process, along with the underlying mathematical principles, is vital for various applications in everyday life, academics, and professional settings. By mastering this skill, you build a strong foundation in mathematical literacy, allowing you to confidently handle similar calculations and apply your knowledge to a wide range of problems. Remember, consistent practice is crucial for solidifying your understanding and improving your problem-solving skills related to fractions and percentages.
Latest Posts
Latest Posts
-
Can You Have Negative Fractions
Sep 18, 2025
-
1 3 4 To Decimal
Sep 18, 2025
-
Is 7 8 Greater Than 5 8
Sep 18, 2025
-
What Percent Is 1 10
Sep 18, 2025
-
What Is 5 6 Of 3 4
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 4 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.