Is 7/8 Greater Than 5/8
saludintensiva
Sep 18, 2025 · 5 min read
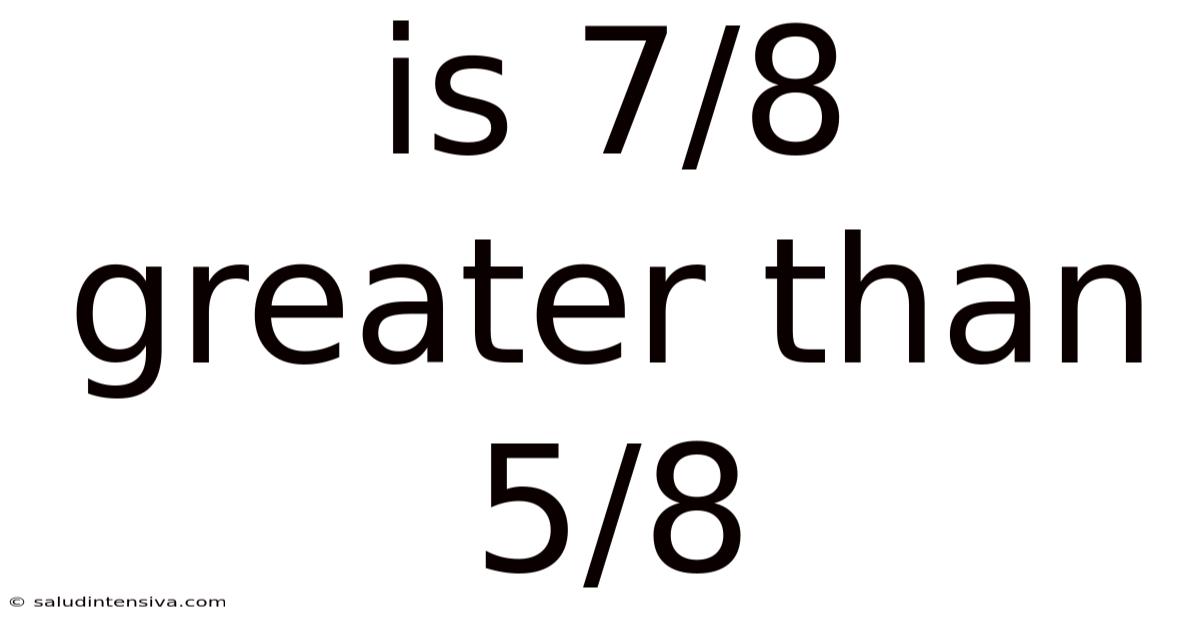
Table of Contents
Is 7/8 Greater Than 5/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to understanding complex financial models. This article will thoroughly explore the seemingly simple question, "Is 7/8 greater than 5/8?", and delve into the underlying concepts of fraction comparison, providing a comprehensive understanding for learners of all levels. We'll explore various methods for comparing fractions, examining both visual representations and numerical approaches. This will build a strong foundation for tackling more complex fraction problems in the future.
Understanding Fractions: A Quick Refresher
Before we dive into the comparison, let's quickly review what fractions represent. A fraction is a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, and the numerator tells us how many of those parts we have.
For example, in the fraction 7/8, the denominator 8 indicates that the whole is divided into 8 equal parts. The numerator 7 shows that we have 7 of those 8 parts. Similarly, 5/8 represents 5 out of 8 equal parts of the whole.
Visualizing the Comparison: The Power of Diagrams
One of the easiest ways to compare fractions is to visualize them. Imagine a pizza cut into 8 equal slices. 7/8 represents having 7 slices, while 5/8 represents having 5 slices. Clearly, having 7 slices is more than having 5 slices. This simple visual representation makes it immediately apparent that 7/8 is greater than 5/8.
We can represent this visually with a diagram:
[Imagine a diagram here showing two circles. One circle has 7 out of 8 slices shaded, the other has 5 out of 8 slices shaded. The shaded areas clearly show that 7/8 is larger.]
Comparing Fractions with the Same Denominator
The problem presented, 7/8 and 5/8, offers a particularly straightforward comparison. Both fractions have the same denominator (8). When comparing fractions with the same denominator, the fraction with the larger numerator is the larger fraction. Since 7 is greater than 5, 7/8 is greater than 5/8. This is a fundamental rule for comparing fractions.
Numerical Comparison: A Step-by-Step Approach
While visualization is helpful, a numerical approach provides a more formal and generalizable method for comparing fractions. This method is particularly useful when dealing with fractions that don't have the same denominator. However, it is equally applicable to our example.
Step 1: Check the Denominators
In our case, the denominators are already the same (both are 8). This simplifies the comparison significantly.
Step 2: Compare the Numerators
Compare the numerators: 7 and 5. Since 7 > 5, the fraction 7/8 is greater than 5/8.
Comparing Fractions with Different Denominators: A More Advanced Approach
Let's extend our understanding to scenarios where fractions have different denominators. For example, let's compare 2/3 and 3/4. Here, we can't directly compare the numerators because the denominators are different. We need to find a common denominator.
Finding a Common Denominator
A common denominator is a number that is a multiple of both denominators. In our example, the least common multiple (LCM) of 3 and 4 is 12.
Converting to Equivalent Fractions
We convert both fractions to equivalent fractions with a denominator of 12:
- 2/3 = (2 x 4) / (3 x 4) = 8/12
- 3/4 = (3 x 3) / (4 x 3) = 9/12
Comparing the Equivalent Fractions
Now we can easily compare the equivalent fractions: 8/12 and 9/12. Since 9 > 8, 9/12 (or 3/4) is greater than 8/12 (or 2/3).
Decimal Representation: Another Method of Comparison
Fractions can be expressed as decimals. This can be another way to compare them. Converting 7/8 and 5/8 to decimals:
- 7/8 = 0.875
- 5/8 = 0.625
Comparing the decimal values, it's clear that 0.875 > 0.625, confirming that 7/8 > 5/8. This method is particularly useful when dealing with fractions that are difficult to visualize or convert to a common denominator.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is a fundamental building block in mathematics. It's not just about solving simple problems; it's about developing a strong understanding of numerical relationships and proportional reasoning. This skill is essential for success in higher-level math courses, including algebra, geometry, and calculus. Furthermore, it has real-world applications in numerous fields, from finance and engineering to cooking and construction.
Frequently Asked Questions (FAQ)
Q1: Can I always use the visual method to compare fractions?
A1: While the visual method is excellent for understanding the basic concept, it becomes less practical and less precise when dealing with larger or more complex fractions. Numerical methods are more reliable for accurate comparison.
Q2: What if the fractions have very large denominators?
A2: Finding a common denominator might become tedious with very large denominators. In such cases, converting to decimals can be a more efficient approach. Alternatively, you could simplify the fractions first if possible.
Q3: Are there any other ways to compare fractions besides these methods?
A3: Yes, there are other advanced techniques, such as cross-multiplication, which can be used to compare fractions efficiently. However, the methods discussed above provide a solid foundation for understanding fraction comparison.
Q4: Why is understanding fractions so important?
A4: Understanding fractions is fundamental to many areas of mathematics and has numerous real-world applications in fields such as measurement, finance, and science. A strong understanding of fractions ensures a solid foundation for more advanced mathematical concepts.
Conclusion: Mastering Fraction Comparison
We've explored multiple ways to determine that 7/8 is indeed greater than 5/8. This seemingly simple question has served as a springboard to explore the fundamental principles of fraction comparison. From visual representations to numerical approaches and decimal conversions, we've covered various strategies to help you confidently compare fractions. Mastering these techniques will not only improve your mathematical skills but also enhance your problem-solving abilities in various contexts. Remember, the key to mastering fractions lies in understanding the underlying concepts and practicing regularly. With consistent effort, you'll build a strong foundation in this crucial area of mathematics.
Latest Posts
Latest Posts
-
13 6 As A Mixed Number
Sep 18, 2025
-
8am 1pm Is How Many Hours
Sep 18, 2025
-
1 1 3 In Simplest Form
Sep 18, 2025
-
2 15 As A Percent
Sep 18, 2025
-
Finding Roots Of Polynomials Calculator
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 7/8 Greater Than 5/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.