13/6 As A Mixed Number
saludintensiva
Sep 18, 2025 · 6 min read
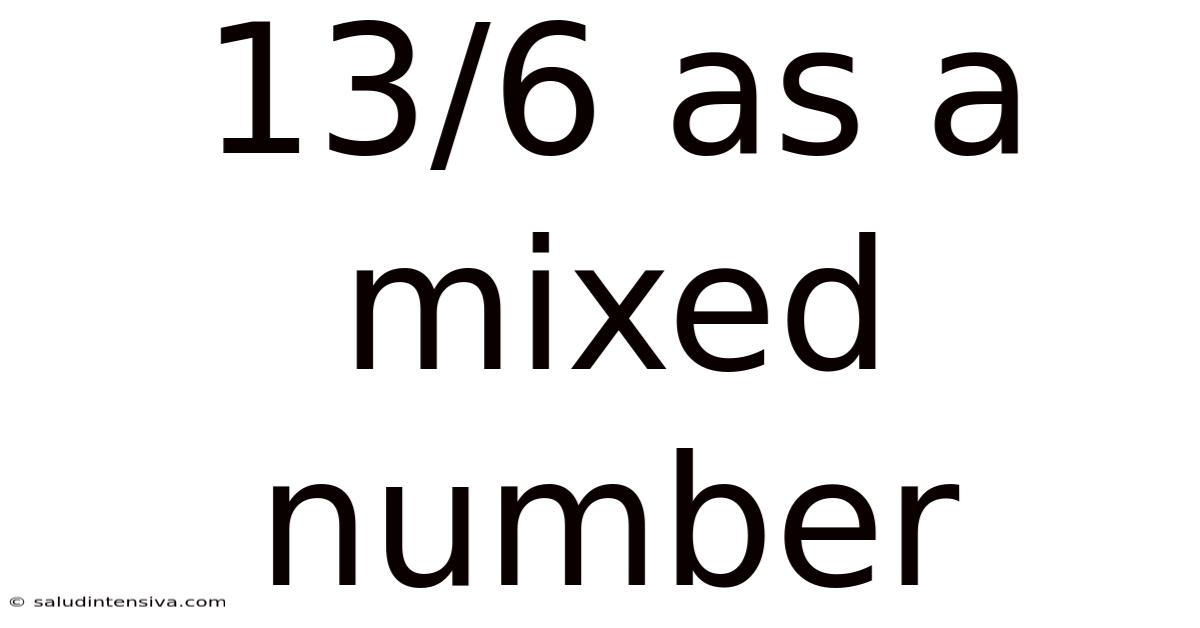
Table of Contents
Understanding 13/6 as a Mixed Number: A Comprehensive Guide
The improper fraction 13/6, where the numerator (13) is larger than the denominator (6), can be expressed as a mixed number. This guide will thoroughly explain the process of converting improper fractions to mixed numbers, focusing specifically on 13/6, and delve into the underlying mathematical concepts. Understanding this conversion is crucial for mastering fundamental arithmetic and building a solid foundation in mathematics. We'll cover the steps involved, provide examples, explore the practical applications of mixed numbers, and address frequently asked questions.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is smaller than the denominator (e.g., 1/2, 3/4, 5/8). A mixed number is a convenient way to represent quantities that are greater than one whole unit. For instance, if you have one whole pizza and half of another, you can represent this as 1 ½. This is a more intuitive representation than the equivalent improper fraction of 3/2.
Converting 13/6 to a Mixed Number: A Step-by-Step Guide
Converting an improper fraction like 13/6 into a mixed number involves dividing the numerator by the denominator. Here's how to do it:
-
Divide the Numerator by the Denominator: Divide 13 by 6. This gives us a quotient and a remainder.
13 ÷ 6 = 2 with a remainder of 1
-
Identify the Whole Number: The quotient (2) becomes the whole number part of the mixed number.
-
Identify the Fraction: The remainder (1) becomes the numerator of the fraction, and the original denominator (6) remains the denominator. This gives us the fraction 1/6.
-
Combine the Whole Number and the Fraction: Combine the whole number and the fraction to form the mixed number. Therefore, 13/6 expressed as a mixed number is 2 1/6.
Visual Representation of 13/6
Imagine you have 13 equally sized slices of pizza. Since there are 6 slices in a whole pizza, you can make two complete pizzas (12 slices, 6 slices per pizza) with 1 slice left over. This leftover slice represents 1/6 of a pizza. Thus, the visual representation strongly reinforces the mathematical conversion: two whole pizzas and 1/6 of a pizza.
Understanding the Mathematical Principles Behind the Conversion
The conversion from an improper fraction to a mixed number relies on the principle of expressing a quantity in different but equivalent forms. The improper fraction 13/6 represents 13 divided into 6 equal parts. Performing the division (13 ÷ 6) helps us understand how many whole units (pizzas in our example) are contained within that quantity, and what portion of a whole unit remains.
The conversion can also be understood using the concept of equivalent fractions. We can rewrite 13/6 as the sum of two fractions:
13/6 = 12/6 + 1/6
Since 12/6 simplifies to 2 (because 12 divided by 6 equals 2), we have:
13/6 = 2 + 1/6 = 2 1/6
Practical Applications of Mixed Numbers
Mixed numbers are incredibly useful in various real-world applications. They offer a more intuitive and practical way to represent quantities than improper fractions. Here are a few examples:
- Measurement: Imagine measuring ingredients for a recipe. If a recipe calls for 2 1/4 cups of flour, using the mixed number is far easier to understand and measure than using the improper fraction 9/4.
- Time: Representing time often involves mixed numbers. For example, 1 hour and 30 minutes can be written as 1 ½ hours.
- Construction: In construction and carpentry, measurements often utilize mixed numbers for precision and ease of understanding.
- Everyday Life: Many daily activities involve quantities best represented by mixed numbers, from baking to sewing to sharing resources.
Working with Mixed Numbers: Addition and Subtraction
Once you have converted an improper fraction to a mixed number, you can perform arithmetic operations more easily. However, when adding or subtracting mixed numbers, it's often simpler to convert them back into improper fractions first. For example:
To add 2 1/6 + 1 1/3, first convert both mixed numbers to improper fractions:
2 1/6 = (2 * 6 + 1) / 6 = 13/6
1 1/3 = (1 * 3 + 1) / 3 = 4/3
Now find a common denominator (6):
4/3 = 8/6
Add the improper fractions:
13/6 + 8/6 = 21/6
Then convert the result back to a mixed number:
21/6 = 3 3/6 = 3 1/2
Working with Mixed Numbers: Multiplication and Division
Multiplication and division with mixed numbers also frequently benefit from initial conversion to improper fractions. This simplifies the calculations significantly. For example, consider multiplying 2 1/6 by 3/2:
First, convert 2 1/6 to an improper fraction: 13/6
Then, perform the multiplication:
(13/6) * (3/2) = 39/12
Finally, simplify and convert back to a mixed number:
39/12 = 13/4 = 3 1/4
Frequently Asked Questions (FAQs)
Q1: Why is it important to learn how to convert improper fractions to mixed numbers?
A1: Converting improper fractions to mixed numbers provides a more intuitive and practical representation of quantities greater than one. It simplifies arithmetic operations and improves understanding in various real-world applications.
Q2: Can all improper fractions be converted to mixed numbers?
A2: Yes, all improper fractions can be converted to mixed numbers. The process involves dividing the numerator by the denominator and expressing the result as a whole number and a fraction.
Q3: What if the remainder is zero after dividing the numerator by the denominator?
A3: If the remainder is zero, it means the improper fraction is actually a whole number. For instance, 12/6 = 2. There is no fractional part in the mixed number representation.
Q4: Are there other ways to represent 13/6 besides 2 1/6?
A4: While 2 1/6 is the simplest form, you could technically represent it as other equivalent mixed numbers, although they will be less practical. For example, if you were working with twelfths, you could express it as 2 2/12 but it is always better practice to simplify the fraction within the mixed number.
Q5: How can I practice converting improper fractions to mixed numbers?
A5: Practice is key! Start with simple examples and gradually increase the complexity. You can find numerous online resources, worksheets, and practice problems to enhance your skills.
Conclusion
Converting improper fractions to mixed numbers is a fundamental skill in mathematics with far-reaching applications. Understanding the process, the underlying mathematical principles, and its practical applications empowers you to tackle various real-world problems involving quantities greater than one. By mastering this skill, you build a strong foundation for more advanced mathematical concepts. Remember to practice regularly and utilize different methods (visual, numerical, and conceptual) to solidify your understanding. The ability to work confidently with mixed numbers will greatly benefit you in many areas of your life, from cooking and construction to more complex mathematical studies.
Latest Posts
Latest Posts
-
2 And 1 8 Inches
Sep 18, 2025
-
What Is 2 5 Of 2 3
Sep 18, 2025
-
Lcm Of 13 And 12
Sep 18, 2025
-
Gcf Of 45 And 30
Sep 18, 2025
-
29 2 As A Decimal
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 13/6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.