What Is 2/5 Of 2/3
saludintensiva
Sep 18, 2025 · 5 min read
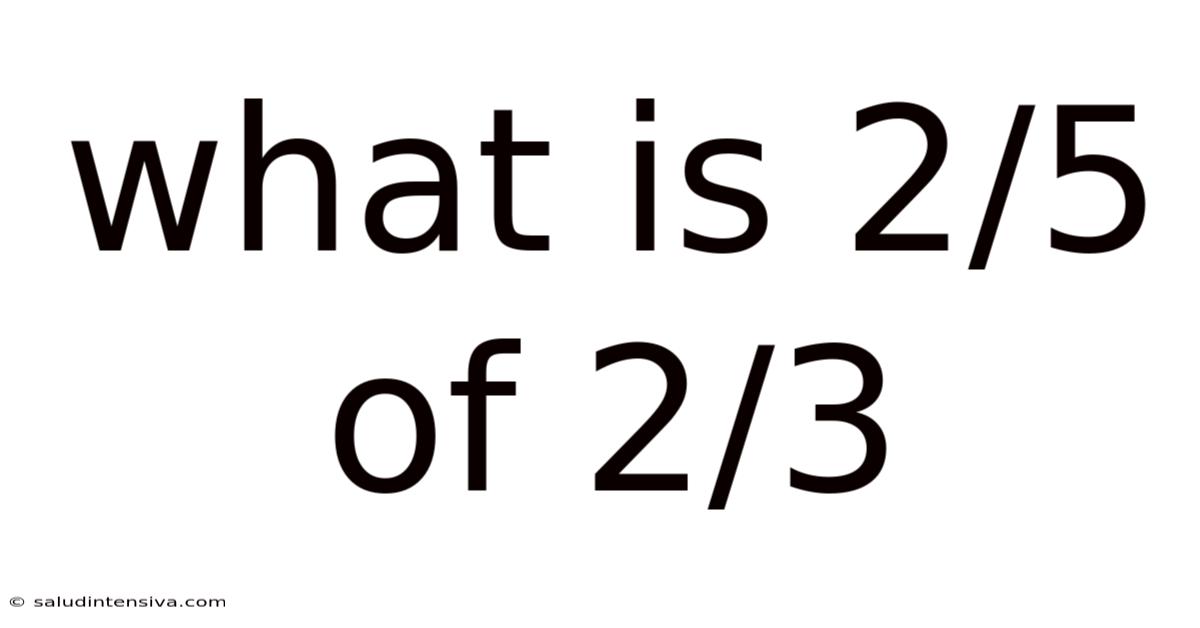
Table of Contents
Unlocking the Mystery: What is 2/5 of 2/3? A Deep Dive into Fraction Multiplication
Understanding fractions is a cornerstone of mathematics, crucial for everything from baking a cake to calculating complex engineering projects. This article will delve into the seemingly simple question: "What is 2/5 of 2/3?" We'll not only provide the answer but also explore the underlying principles of fraction multiplication, offering a comprehensive understanding that goes beyond rote memorization. This will equip you with the skills to tackle similar problems with confidence and even delve into more advanced fractional calculations.
Understanding Fractions: A Quick Refresher
Before we tackle the main problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts we're considering. For example, in the fraction 2/3, the denominator (3) means the whole is divided into three equal parts, and the numerator (2) means we're considering two of those parts.
The "Of" Means Multiplication
The word "of" in mathematics, when used with fractions, signifies multiplication. Therefore, "2/5 of 2/3" translates directly to (2/5) x (2/3). This seemingly simple translation opens the door to understanding how to solve this type of problem.
Step-by-Step Solution: Multiplying Fractions
The process of multiplying fractions is straightforward:
-
Multiply the Numerators: Multiply the top numbers (numerators) together. In our case, this is 2 x 2 = 4.
-
Multiply the Denominators: Multiply the bottom numbers (denominators) together. Here, it's 5 x 3 = 15.
-
Form the Resultant Fraction: Combine the results from steps 1 and 2 to form the new fraction. This gives us 4/15.
Therefore, 2/5 of 2/3 is 4/15.
Visualizing the Multiplication: A Geometric Approach
Understanding fraction multiplication can be enhanced by visualizing it geometrically. Imagine a rectangle representing the whole. Dividing this rectangle into thirds (representing the 2/3) and then taking two-fifths of those thirds provides a clear visual representation of the final result, 4/15. You would divide the rectangle into 15 equal pieces (5 rows of 3 columns) and shade 4 of these, thus confirming our mathematical result. This visual approach helps solidify the concept and makes it more intuitive.
Simplifying Fractions: Finding the Simplest Form
While 4/15 is a perfectly valid answer, it's good practice to simplify fractions to their simplest form whenever possible. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. In our case, the GCD of 4 and 15 is 1, meaning our fraction is already in its simplest form. However, if we had a fraction like 6/12, we would simplify it by dividing both the numerator and denominator by their GCD (which is 6), resulting in the simplified fraction 1/2.
Extending the Concept: Multiplying More Than Two Fractions
The principle of multiplying fractions extends seamlessly to multiplying more than two fractions. The process remains the same: multiply all the numerators together and multiply all the denominators together. For example, to find 1/2 of 2/3 of 3/4, you would calculate (1 x 2 x 3) / (2 x 3 x 4) = 6/24. This then simplifies to 1/4.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical concept; it has numerous real-world applications:
-
Cooking and Baking: Recipes often require fractions of ingredients. Calculating the amount of an ingredient needed when adjusting a recipe size involves fraction multiplication. For instance, if a recipe calls for 1/2 cup of sugar and you want to make half the recipe, you'll need 1/2 of 1/2 cup, which is 1/4 cup.
-
Construction and Engineering: Accurate measurements are essential in construction and engineering. Calculations involving dimensions and materials often involve fraction multiplication.
-
Finance: Calculating percentages, interest rates, and proportions in finance frequently requires working with fractions.
-
Data Analysis: Understanding proportions and ratios in data analysis often involves working with fractions and their multiplication.
Frequently Asked Questions (FAQs)
Q: What if the fractions have different denominators?
A: The process remains the same. You multiply the numerators together and the denominators together. Simplifying the resulting fraction is often necessary.
Q: Can I convert fractions to decimals before multiplying?
A: Yes, you can. Converting fractions to decimals and then multiplying will give the same result. However, working with fractions directly often leads to simpler calculations, especially when dealing with complex fractions.
Q: How can I improve my skills in fraction multiplication?
A: Practice is key! Start with simple problems and gradually increase the complexity. Use visual aids like diagrams or physical objects to understand the concept better. Also, review the rules and methods regularly.
Q: Are there any shortcuts for fraction multiplication?
A: Sometimes, you can simplify the fractions before multiplying. If a numerator and a denominator share a common factor, you can cancel them out. For example, in (2/5) x (15/8), you can cancel out the 2 in the numerator with the 8 in the denominator (leaving 4), and the 5 in the denominator with the 15 in the numerator (leaving 3). This simplifies the calculation to (1/1) x (3/4) = 3/4.
Conclusion: Mastering Fraction Multiplication
Understanding fraction multiplication is a fundamental skill in mathematics with far-reaching applications in various fields. This article has provided a comprehensive guide, covering not only the mechanics of multiplying fractions but also the underlying principles and real-world applications. Remember, mastering fractions involves consistent practice and a willingness to explore different approaches. By understanding the concepts thoroughly and practicing regularly, you can build a solid foundation in mathematics and tackle more complex problems with confidence. The seemingly simple question, "What is 2/5 of 2/3?" has served as a gateway to unlock a deeper understanding of this essential mathematical operation. The answer, 4/15, is only the beginning of a journey into the fascinating world of fractions.
Latest Posts
Latest Posts
-
What Is 8 6 Simplified
Sep 19, 2025
-
Fraction To Percent How To
Sep 19, 2025
-
10 454 Sqft To Acres
Sep 19, 2025
-
3 3 10 As A Decimal
Sep 19, 2025
-
9 10 As A Percentage
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/5 Of 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.