What Is 5/6 Of 3/4
saludintensiva
Sep 18, 2025 · 6 min read
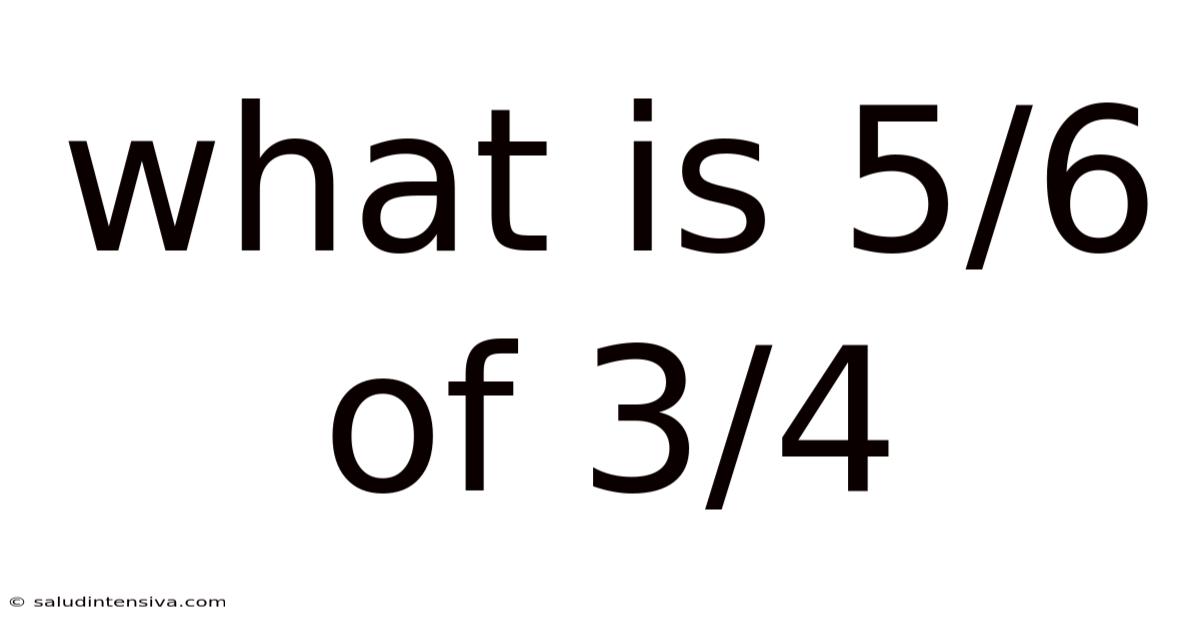
Table of Contents
What is 5/6 of 3/4? A Deep Dive into Fraction Multiplication
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to calculating complex engineering projects. This article explores the seemingly simple question, "What is 5/6 of 3/4?", but goes beyond a simple answer to provide a comprehensive understanding of fraction multiplication, including its practical applications and common pitfalls. We'll delve into the mechanics of the calculation, explore the underlying mathematical principles, and address frequently asked questions. By the end, you'll not only know the answer but also possess a deeper understanding of how to tackle similar problems with confidence.
Understanding Fractions: A Quick Refresher
Before tackling the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many parts we have, while the denominator tells us how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3 and the denominator is 4. This means we have 3 out of 4 equal parts.
Multiplying Fractions: The Core Concept
Multiplying fractions is a relatively straightforward process. To multiply two fractions, we simply multiply the numerators together and multiply the denominators together. This can be represented mathematically as:
(a/b) * (c/d) = (a * c) / (b * d)
Where 'a', 'b', 'c', and 'd' are integers, and 'b' and 'd' are not equal to zero (as division by zero is undefined).
Solving the Problem: 5/6 of 3/4
Now, let's apply this knowledge to the problem at hand: What is 5/6 of 3/4? The word "of" in this context means "multiply". Therefore, we need to multiply 5/6 by 3/4:
(5/6) * (3/4) = (5 * 3) / (6 * 4) = 15/24
So, 5/6 of 3/4 is 15/24.
Simplifying Fractions: Finding the Lowest Terms
The fraction 15/24 is a correct answer, but it's not in its simplest form. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and denominator and divide both by it.
The GCD of 15 and 24 is 3. Dividing both the numerator and denominator by 3, we get:
15/3 = 5 and 24/3 = 8
Therefore, the simplified answer is 5/8. This represents the simplest and most concise way to express the result of the multiplication.
Visualizing Fraction Multiplication: A Geometric Approach
Understanding fraction multiplication can be enhanced by visualizing it geometrically. Imagine a rectangle representing the whole (1). We can divide this rectangle into 4 equal parts horizontally to represent 3/4. Then, we can divide each of these 4 parts into 6 equal parts vertically to represent 5/6. The resulting area that is both shaded horizontally (3/4) and vertically (5/6) will represent the product of the two fractions. Counting the number of small squares that fit this criteria and comparing it to the total number of squares within the entire rectangle will provide a visual representation of the answer, 5/8.
Practical Applications of Fraction Multiplication
Fraction multiplication finds applications in numerous real-world scenarios:
- Cooking and Baking: Scaling recipes up or down requires multiplying fractional amounts of ingredients.
- Construction and Engineering: Calculating material quantities, proportions, and measurements often involves fractions.
- Finance: Calculating percentages, interest rates, and portions of investments frequently utilize fraction multiplication.
- Everyday Life: Sharing items equally or calculating parts of a whole, such as dividing a pizza among friends, involves fractional concepts.
Understanding fraction multiplication enables you to confidently and accurately tackle these everyday challenges.
Common Mistakes in Fraction Multiplication
Even though the process seems straightforward, several common mistakes can occur:
- Forgetting to multiply both the numerators and the denominators: Only multiplying the numerators or the denominators will lead to an incorrect result.
- Incorrectly simplifying fractions: Failing to find the GCD or dividing by an incorrect common factor will result in a simplified fraction that is not in its lowest terms.
- Not understanding the concept of "of": Failing to recognize that "of" in this context means multiplication can lead to an incorrect approach to the problem.
- Difficulty visualizing fractions: A lack of visualization skills can impede the ability to understand and solve fraction problems.
Frequently Asked Questions (FAQs)
Q: Can I multiply fractions in any order?
A: Yes, fraction multiplication is commutative, meaning the order doesn't matter. (5/6) * (3/4) is the same as (3/4) * (5/6).
Q: What if one of the fractions is a whole number?
A: Treat the whole number as a fraction with a denominator of 1. For example, to find 2/3 of 5, you would calculate (2/3) * (5/1) = 10/3.
Q: What if I have more than two fractions to multiply?
A: Multiply the numerators together and multiply the denominators together. Simplify the resulting fraction to its lowest terms.
Q: Is there an easier way to simplify fractions?
A: Besides finding the GCD, you can cancel out common factors between the numerator and denominator before multiplying. For example, in (5/6) * (3/4), we can cancel the 3 in the numerator and the 6 in the denominator (dividing both by 3) to get (5/2) * (1/4) = 5/8. This method simplifies the calculation and reduces the chance of errors.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through numerous problems of varying difficulty. Utilize visual aids, such as diagrams and manipulatives. Explore online resources and educational videos. Break down complex problems into simpler steps. Seek help from teachers or tutors if needed.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a cornerstone of mathematical literacy. By understanding the underlying principles, practicing regularly, and avoiding common pitfalls, you can confidently tackle fraction multiplication problems. This article provided a comprehensive approach to solving "What is 5/6 of 3/4?", demonstrating the steps involved, offering visualizations, and addressing common questions. Remember, the key to success lies in consistent practice and a thorough understanding of the concepts. The seemingly simple problem of multiplying 5/6 by 3/4 serves as a gateway to a broader understanding of fractions and their diverse applications in our world. Continue to explore and practice, and you will find that the world of fractions becomes increasingly accessible and even enjoyable!
Latest Posts
Latest Posts
-
8am 1pm Is How Many Hours
Sep 18, 2025
-
1 1 3 In Simplest Form
Sep 18, 2025
-
2 15 As A Percent
Sep 18, 2025
-
Finding Roots Of Polynomials Calculator
Sep 18, 2025
-
38 1 Degrees Celsius To Fahrenheit
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 5/6 Of 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.