12/6 As A Mixed Number
saludintensiva
Sep 15, 2025 · 6 min read
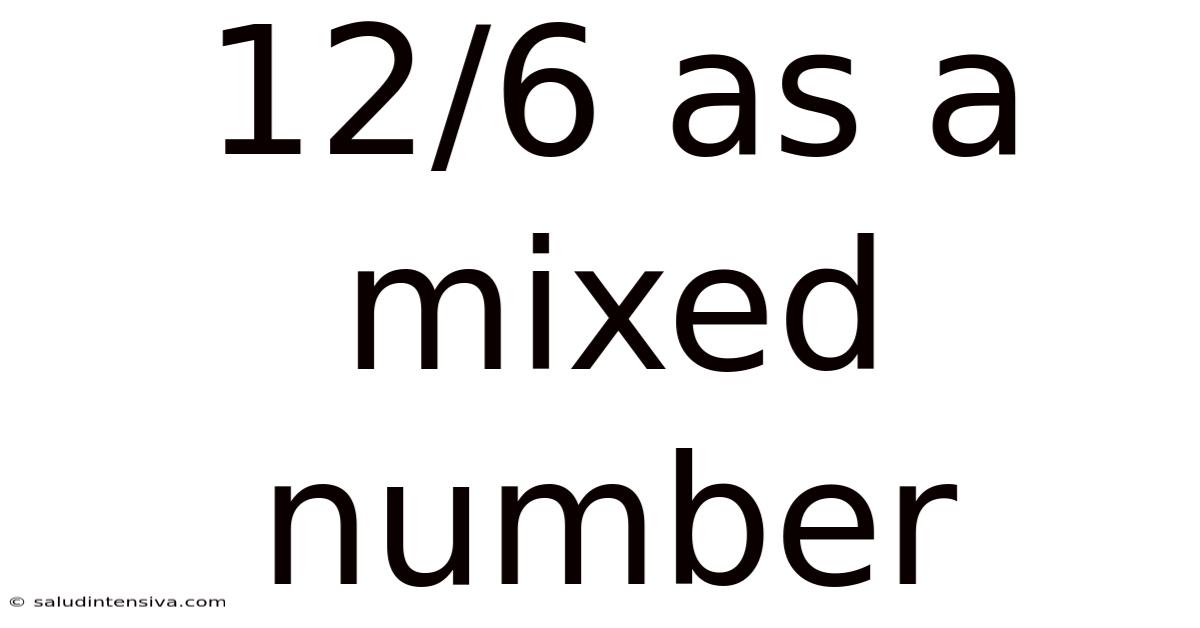
Table of Contents
Understanding 12/6 as a Mixed Number: A Comprehensive Guide
The fraction 12/6, while seemingly simple, presents a valuable opportunity to understand the concept of improper fractions and their conversion to mixed numbers. This guide will delve into the meaning of 12/6, explain the process of converting improper fractions to mixed numbers, and explore the underlying mathematical principles. We'll also address frequently asked questions to ensure a complete understanding of this fundamental arithmetic concept. By the end, you'll not only know the mixed number equivalent of 12/6 but also possess a solid grasp of the broader principles involved.
Introduction to Fractions: A Quick Refresher
Before diving into the specifics of 12/6, let's briefly review the fundamental components of a fraction. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, representing the number of parts we have.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) indicates we have three parts, and the denominator (4) indicates the whole is divided into four equal parts.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. This means it represents a value greater than or equal to one whole. 12/6 is an example of an improper fraction because the numerator (12) is larger than the denominator (6). Improper fractions are perfectly valid, but they are often expressed more intuitively as mixed numbers.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). It represents a value greater than one. For instance, 2 1/2 is a mixed number; it signifies two whole units plus one-half of another unit.
Converting 12/6 to a Mixed Number
The process of converting an improper fraction like 12/6 to a mixed number involves dividing the numerator by the denominator.
-
Divide: Divide the numerator (12) by the denominator (6): 12 ÷ 6 = 2
-
Whole Number: The quotient (2) becomes the whole number part of the mixed number.
-
Remainder (if any): If there's a remainder, it becomes the numerator of the fractional part. In this case, there is no remainder as the division is exact.
-
Denominator: The denominator of the mixed number remains the same as the original fraction's denominator (6). Since there is no remainder, there is no fractional part.
Therefore, 12/6 as a mixed number is simply 2.
Understanding the Concept: Visual Representation
Imagine you have 12 equally sized slices of pizza. If each pizza has 6 slices, how many pizzas do you have? You have 12 slices / 6 slices/pizza = 2 pizzas. This visually demonstrates that 12/6 is equivalent to 2.
Beyond 12/6: Converting Other Improper Fractions
Let's practice with another example: Convert 17/5 to a mixed number.
-
Divide: 17 ÷ 5 = 3 with a remainder of 2.
-
Whole Number: The quotient (3) is the whole number part.
-
Remainder: The remainder (2) becomes the numerator of the fractional part.
-
Denominator: The denominator remains 5.
Therefore, 17/5 as a mixed number is 3 2/5.
Another Example: 22/7
Let's try a more complex example: Convert 22/7 to a mixed number.
-
Divide: 22 ÷ 7 = 3 with a remainder of 1.
-
Whole Number: The quotient (3) is the whole number part.
-
Remainder: The remainder (1) becomes the numerator of the fractional part.
-
Denominator: The denominator remains 7.
Therefore, 22/7 as a mixed number is 3 1/7.
Simplifying Fractions Before Conversion
Sometimes, it's beneficial to simplify the fraction before converting it to a mixed number. This makes the division process easier. For example, consider the improper fraction 24/8. We can simplify this by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 8: 24/8 simplifies to 3/1, which is simply 3.
The Importance of Mixed Numbers
Mixed numbers are valuable because they offer a more intuitive way to represent quantities greater than one. While improper fractions are perfectly acceptable mathematically, mixed numbers provide a clearer visual and practical understanding of the value. Imagine explaining that you have 17/5 of a pizza – it's less clear than saying you have 3 2/5 pizzas.
Converting Mixed Numbers Back to Improper Fractions
It's also important to understand how to convert a mixed number back into an improper fraction. Here's the process:
-
Multiply: Multiply the whole number by the denominator.
-
Add: Add the result to the numerator.
-
Denominator: The denominator remains the same.
Let's convert 3 2/5 back to an improper fraction:
-
Multiply: 3 * 5 = 15
-
Add: 15 + 2 = 17
-
Denominator: The denominator remains 5.
Therefore, 3 2/5 as an improper fraction is 17/5.
Frequently Asked Questions (FAQ)
Q: Why is it important to learn about improper fractions and mixed numbers?
A: Understanding improper fractions and mixed numbers is crucial for a solid foundation in arithmetic and further mathematical concepts. They are essential for working with fractions, solving problems involving quantities greater than one, and understanding more advanced mathematical topics.
Q: Can all improper fractions be converted to mixed numbers?
A: Yes, all improper fractions can be converted to mixed numbers, except for those where the numerator is exactly a multiple of the denominator, resulting in a whole number. As we saw with 12/6, the result is simply a whole number (2).
Q: What if I get a decimal in the division step?
A: If you get a decimal during division, it indicates that the fraction can be simplified further or that the division is not exact. You should consider simplifying the fraction first. If the decimal is non-terminating (e.g., 1/3 = 0.333...), then the remainder forms the fractional part of the mixed number.
Q: Are there other ways to represent fractions besides improper fractions and mixed numbers?
A: Yes! Fractions can also be represented as decimals (e.g., 1/2 = 0.5) or percentages (e.g., 1/2 = 50%). Each representation has its own advantages and applications.
Conclusion
Understanding the relationship between improper fractions and mixed numbers is a fundamental skill in mathematics. This comprehensive guide has explored the concept of converting improper fractions, such as 12/6, to mixed numbers, providing clear explanations, visual aids, and practical examples. The process is straightforward: divide the numerator by the denominator, use the quotient as the whole number, and any remainder becomes the numerator of the fractional part. Mastering this skill will significantly enhance your understanding of fractions and prepare you for more advanced mathematical concepts. Remember to practice regularly to build confidence and fluency in these essential arithmetic procedures.
Latest Posts
Latest Posts
-
Is 7 8 Greater Than 1 2
Sep 15, 2025
-
1 2 Minus 3 4
Sep 15, 2025
-
What Is 1 4 Percentage
Sep 15, 2025
-
Calculate Variance Of A Portfolio
Sep 15, 2025
-
Fractions Equivalent To 3 10
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 12/6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.