12 Divided By 5 2/5
saludintensiva
Sep 22, 2025 · 5 min read
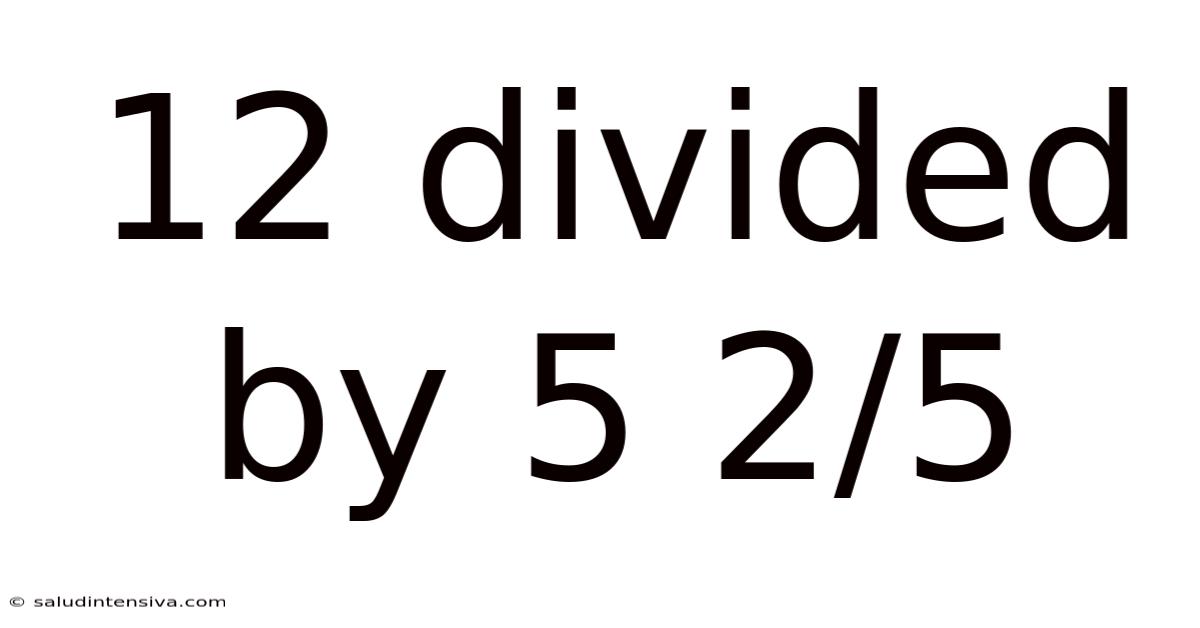
Table of Contents
Solving the Division Problem: 12 Divided by 5 2/5
Dividing fractions and mixed numbers can seem daunting, but with a structured approach, it becomes a straightforward process. This article will guide you through solving the problem "12 divided by 5 2/5," explaining each step in detail and providing a deeper understanding of the underlying mathematical principles. We'll cover the conversion of mixed numbers to improper fractions, the reciprocal method of division, and simplification techniques, ultimately arriving at the correct answer and exploring related concepts. This comprehensive guide is designed for anyone, from students brushing up on their math skills to those seeking a refresher on fraction division.
Understanding the Problem: 12 ÷ 5 2/5
Before we dive into the solution, let's break down the problem itself: 12 ÷ 5 2/5. This represents a division problem where 12 (a whole number) is being divided by 5 2/5 (a mixed number). To solve this accurately, we need to convert the mixed number into an improper fraction and then apply the rules of fraction division. This process allows for a consistent and reliable calculation.
Step 1: Converting the Mixed Number to an Improper Fraction
A mixed number, like 5 2/5, combines a whole number (5) and a proper fraction (2/5). To convert it into an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 5 x 5 = 25
- Add the numerator to the result: 25 + 2 = 27
- Keep the same denominator: The denominator remains 5.
Therefore, 5 2/5 is equivalent to the improper fraction 27/5. Our problem now becomes: 12 ÷ 27/5.
Step 2: Converting the Whole Number to a Fraction
To perform division with fractions, it's helpful to express all numbers as fractions. The whole number 12 can be written as a fraction with a denominator of 1: 12/1. Now our problem is: 12/1 ÷ 27/5.
Step 3: Applying the Reciprocal Method of Fraction Division
Dividing fractions involves a crucial step: we don't directly divide the numerators and denominators. Instead, we multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is obtained by swapping its numerator and denominator.
The reciprocal of 27/5 is 5/27. So, our problem transforms into a multiplication problem:
12/1 x 5/27
Step 4: Performing the Multiplication
Now we multiply the numerators together and the denominators together:
(12 x 5) / (1 x 27) = 60/27
Step 5: Simplifying the Fraction
The fraction 60/27 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of 60 and 27. The GCD is 3. We divide both the numerator and the denominator by 3:
60 ÷ 3 = 20 27 ÷ 3 = 9
This simplifies the fraction to 20/9.
Step 6: Converting the Improper Fraction to a Mixed Number (Optional)
While 20/9 is a perfectly valid answer, it's often more convenient to express the answer as a mixed number. To do this:
- Divide the numerator by the denominator: 20 ÷ 9 = 2 with a remainder of 2.
- The quotient becomes the whole number: 2
- The remainder becomes the numerator of the fraction: 2
- The denominator remains the same: 9
Therefore, 20/9 as a mixed number is 2 2/9.
The Final Answer: 2 2/9
After following these steps, we arrive at the final answer: 12 divided by 5 2/5 equals 2 2/9. This represents the accurate and simplified solution to the given division problem.
A Deeper Dive into the Mathematics
The method used above relies on the fundamental principles of fraction arithmetic. Let's explore these in more detail:
-
Improper Fractions: Improper fractions (where the numerator is larger than or equal to the denominator) are essential for performing division with mixed numbers. They provide a single-unit representation, facilitating easier calculations.
-
Reciprocals: The reciprocal method of division stems from the definition of division itself. Dividing by a fraction is equivalent to multiplying by its reciprocal. This simplifies the process and avoids the complexities of directly dividing fractions.
-
Greatest Common Divisor (GCD): Finding the GCD is crucial for simplifying fractions to their lowest terms. This makes the answer more manageable and easier to interpret. Various methods exist for finding the GCD, including the Euclidean algorithm.
-
Mixed Numbers: Mixed numbers offer a convenient way to represent a combination of whole numbers and fractions. Converting between improper fractions and mixed numbers allows flexibility in problem-solving.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, most calculators can handle fraction division. However, understanding the manual process is crucial for grasping the underlying mathematical concepts. Using a calculator should be seen as a verification tool, not a replacement for learning the method.
Q: What if the numbers were different? How would the process change?
A: The process remains the same regardless of the specific numbers. You'll always convert mixed numbers to improper fractions, find the reciprocal of the divisor, multiply, and simplify the resulting fraction.
Q: Why is the reciprocal used in fraction division?
A: The reciprocal method is a consequence of the inverse relationship between multiplication and division. Multiplying by the reciprocal essentially "undoes" the division operation, leading to the correct result.
Q: Are there alternative methods for solving this problem?
A: While the method described above is the most common and efficient, other approaches exist, but they generally involve the same fundamental steps of converting to improper fractions and applying the principles of fraction arithmetic.
Q: What are some real-world applications of fraction division?
A: Fraction division has wide applications in various fields, including cooking (dividing recipes), construction (measuring materials), and finance (calculating proportions).
Conclusion: Mastering Fraction Division
Solving problems like "12 divided by 5 2/5" requires a methodical approach. By systematically converting mixed numbers to improper fractions, using the reciprocal method for division, and simplifying the resulting fraction, we can confidently arrive at the correct answer. This process reinforces fundamental mathematical principles and provides a solid foundation for tackling more complex fraction problems. Remember, practice is key to mastering this skill, so don't hesitate to try similar problems to solidify your understanding. The ability to confidently work with fractions is a valuable asset in various academic and real-world scenarios.
Latest Posts
Latest Posts
-
32 12 As A Fraction
Sep 22, 2025
-
Days Since August 5 2024
Sep 22, 2025
-
Convert Foot Lbs To Horsepower
Sep 22, 2025
-
What Is 1 3 2 9
Sep 22, 2025
-
Miles Per Gallon To Litres
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 12 Divided By 5 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.