12 Percent As A Fraction
saludintensiva
Sep 14, 2025 · 5 min read
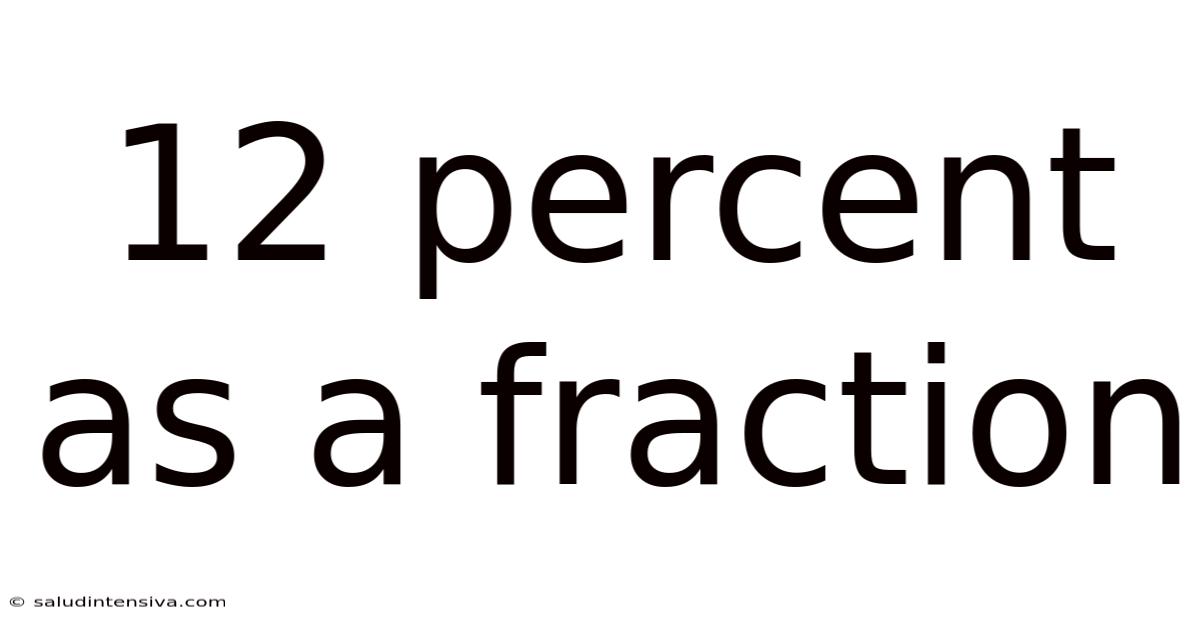
Table of Contents
Understanding 12 Percent as a Fraction: A Comprehensive Guide
Understanding percentages, fractions, and decimals is fundamental to many areas of life, from calculating discounts at the store to understanding financial reports. This comprehensive guide will delve deep into how to represent 12 percent as a fraction, exploring the underlying mathematical concepts and offering various approaches to solve similar problems. We'll move beyond the simple conversion and explore the practical applications of this knowledge. This guide will equip you with the skills to confidently tackle percentage-to-fraction conversions in any context.
What is a Percentage?
Before we dive into converting 12 percent to a fraction, let's solidify our understanding of percentages. A percentage is simply a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 12 percent (written as 12%) means 12 out of 100.
Converting 12% to a Fraction: The Basic Approach
The most straightforward way to convert 12% to a fraction is to remember the definition of percentage. Since 12% means 12 out of 100, we can directly write it as a fraction:
12% = 12/100
This fraction is a perfectly valid representation of 12 percent. However, in mathematics, we often strive to simplify fractions to their lowest terms.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
To simplify 12/100, we need to find the greatest common divisor (GCD) of 12 and 100. The GCD is the largest number that divides both the numerator (12) and the denominator (100) without leaving a remainder.
One way to find the GCD is by listing the factors of each number:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100
The largest number that appears in both lists is 4. Therefore, the GCD of 12 and 100 is 4.
Simplifying 12/100 to its Lowest Terms
Now that we have the GCD, we can simplify the fraction by dividing both the numerator and the denominator by 4:
12 ÷ 4 = 3 100 ÷ 4 = 25
Therefore, the simplified fraction is:
12/100 = 3/25
This is the simplest form of the fraction representing 12%. It means that 12% is equivalent to 3 parts out of 25 equal parts.
Alternative Methods for Conversion
While the method above is the most straightforward, there are alternative approaches to convert percentages to fractions. These methods can be helpful in understanding the underlying concepts and might be preferred depending on individual mathematical skills.
Method 2: Using Decimal Representation
We can convert the percentage to a decimal first, then convert the decimal to a fraction.
-
Convert the percentage to a decimal: To convert a percentage to a decimal, divide by 100. So, 12% becomes 12/100 = 0.12.
-
Convert the decimal to a fraction: The decimal 0.12 can be written as 12/100. This fraction can then be simplified as shown in the previous section to 3/25.
Method 3: Direct Simplification using Prime Factorization
A more advanced, yet efficient, method involves prime factorization. This method is particularly useful for larger percentages or fractions.
-
Prime factorize the numerator and denominator:
- 12 = 2 x 2 x 3
- 100 = 2 x 2 x 5 x 5
-
Cancel out common factors: We can see that both the numerator and denominator share two factors of 2. Cancelling these out, we get:
(2 x 2 x 3) / (2 x 2 x 5 x 5) = 3 / (5 x 5) = 3/25
Practical Applications of Converting Percentages to Fractions
Understanding how to convert percentages to fractions is essential in various real-world scenarios:
-
Cooking and Baking: Recipes often use percentages to indicate the proportion of ingredients. Converting these percentages to fractions can make it easier to measure the ingredients accurately.
-
Finance: Interest rates, discounts, and tax calculations frequently involve percentages. Converting these percentages to fractions allows for easier calculation of the actual amounts.
-
Probability and Statistics: Probabilities are often expressed as percentages. Converting these percentages to fractions provides a clearer understanding of the likelihood of an event occurring.
-
Data Analysis: When working with datasets, percentages might be presented in reports. Converting these percentages to fractions can make it simpler to compare data and draw meaningful conclusions.
-
Geometry and Measurement: Percentages are frequently used in geometry to represent proportions of areas or lengths. Converting these percentages to fractions enables more precise calculations in geometric problems.
Frequently Asked Questions (FAQ)
Q1: Can I convert any percentage to a fraction?
A1: Yes, absolutely! Any percentage can be expressed as a fraction by remembering that a percentage is simply a fraction out of 100.
Q2: What if the resulting fraction is an improper fraction (numerator larger than the denominator)?
A2: If the resulting fraction is improper, you can convert it to a mixed number. For example, if you had 150%, this would become 150/100 which simplifies to 3/2, or 1 ½.
Q3: Are there any online calculators or tools that can help with this conversion?
A3: While numerous online calculators exist for various mathematical operations, the process of converting percentages to fractions is straightforward enough to be done manually, building a strong understanding of the underlying mathematical principles.
Q4: Why is simplifying fractions important?
A4: Simplifying fractions makes them easier to understand and work with. A simplified fraction provides the most concise and efficient representation of a given value.
Q5: How do I convert a fraction back to a percentage?
A5: To convert a fraction back to a percentage, divide the numerator by the denominator and multiply the result by 100. For example, 3/25 = 0.12 x 100 = 12%.
Conclusion
Converting 12 percent to a fraction, which simplifies to 3/25, is a fundamental skill in mathematics with broad applications in various fields. This process reinforces the understanding of percentages, fractions, and the importance of simplifying fractions to their lowest terms. By mastering this conversion, you gain a valuable tool for tackling problems involving proportions, ratios, and quantitative analyses. Remember to practice regularly to solidify your understanding and build confidence in tackling similar problems independently. The various methods outlined in this guide offer different approaches depending on individual preference and mathematical background, ensuring that you'll find the method that best suits your learning style.
Latest Posts
Latest Posts
-
Lcm Of 15 And 75
Sep 14, 2025
-
Lcm Of 8 12 6
Sep 14, 2025
-
7 1 4 Improper Fraction
Sep 14, 2025
-
How Far Is 2 M
Sep 14, 2025
-
9 To The 6 Power
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 12 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.