Lcm Of 8 12 6
saludintensiva
Sep 14, 2025 · 6 min read
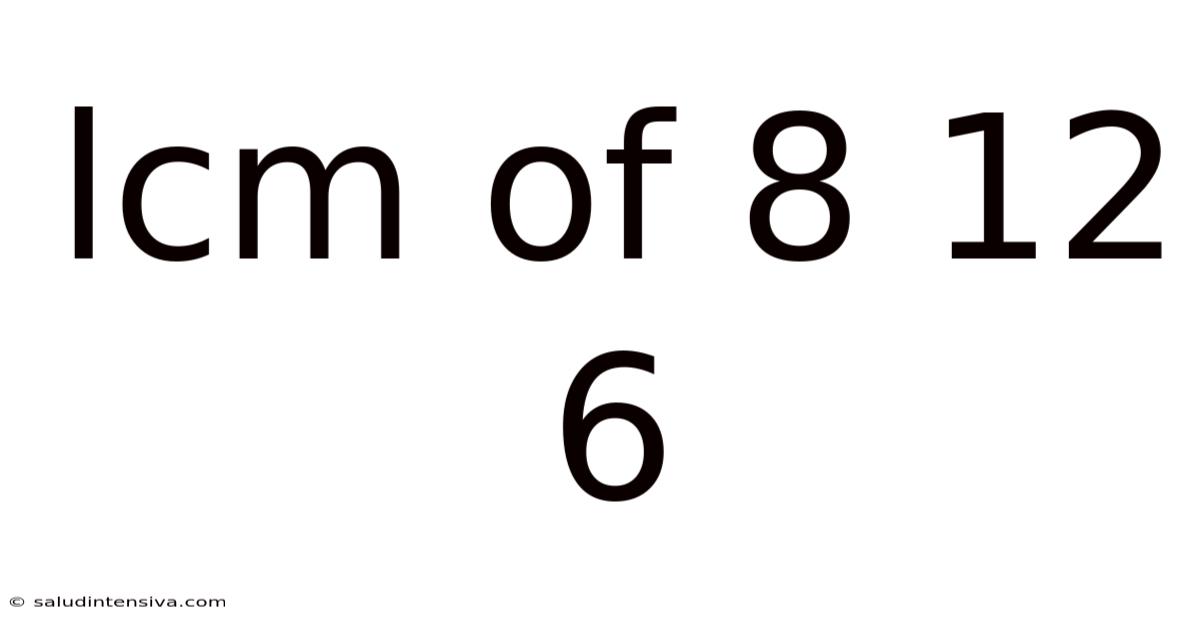
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 12, and 6: A Comprehensive Guide
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and various methods can significantly enhance your mathematical skills and problem-solving abilities. This comprehensive guide will delve into the process of calculating the LCM of 8, 12, and 6, exploring different techniques, explaining the underlying concepts, and answering frequently asked questions. We'll cover everything from basic definitions to advanced strategies, ensuring a thorough understanding of this fundamental concept in number theory.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. Understanding the LCM is crucial in various mathematical applications, including simplifying fractions, solving problems involving time intervals, and understanding rhythmic patterns in music.
Method 1: Listing Multiples
This is a straightforward method, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120...
By comparing the lists, we can see that the smallest number common to all three lists is 24. Therefore, the LCM of 8, 12, and 6 is 24.
Method 2: Prime Factorization
This method is more efficient, especially when dealing with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
-
Prime Factorization:
- 8 = 2³
- 12 = 2² × 3
- 6 = 2 × 3
-
Identify the highest powers of each prime factor:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
-
Multiply the highest powers together:
- LCM(8, 12, 6) = 2³ × 3 = 8 × 3 = 24
Therefore, the LCM of 8, 12, and 6 is 24 using the prime factorization method. This method is generally preferred for its efficiency and applicability to larger numbers.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
The LCM and the Greatest Common Divisor (GCD) are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. While this relationship is most directly applied to two numbers, we can extend it to multiple numbers by applying it iteratively.
-
Find the GCD of 8 and 12:
- Using the Euclidean algorithm:
- 12 = 1 × 8 + 4
- 8 = 2 × 4 + 0
- The GCD(8, 12) = 4
- Using the Euclidean algorithm:
-
Find the LCM of 8 and 12 using the relationship:
- LCM(8, 12) = (8 × 12) / GCD(8, 12) = (96) / 4 = 24
-
Find the GCD of 24 and 6:
- GCD(24, 6) = 6
-
Find the LCM of 24 and 6 using the relationship:
- LCM(24, 6) = (24 × 6) / GCD(24, 6) = (144) / 6 = 24
Therefore, the LCM of 8, 12, and 6 is 24. This iterative approach using the GCD relationship provides another valid and sometimes computationally advantageous method.
Visualizing the LCM
Imagine you have three different types of candies: a pack of 8, a box of 12, and a bag of 6. You want to distribute these candies equally among your friends without having any leftover candies of any type. The LCM represents the minimum number of candies you need to achieve this. In this case, you need 24 candies (three packs of 8, two boxes of 12, or four bags of 6).
Applications of LCM
The LCM has numerous real-world applications:
- Scheduling: Determining when events will occur simultaneously. For example, if one event happens every 8 days and another every 12 days, the LCM helps find when both events will occur on the same day.
- Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is the LCM of the denominators.
- Rhythms and Music: Understanding rhythmic patterns and finding the least common denominator in musical compositions.
- Gear Ratios: Calculating gear ratios in mechanical systems.
- Construction and Engineering: In various calculations related to building materials and dimensions.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The Least Common Multiple (LCM) is the smallest number that is a multiple of all given numbers. The Greatest Common Divisor (GCD) is the largest number that divides all given numbers without leaving a remainder. They are inversely related; a larger LCM implies a smaller GCD, and vice versa.
Q: Can the LCM of two numbers be smaller than one of the numbers?
A: No. The LCM of two or more numbers is always greater than or equal to the largest of the numbers.
Q: What if the numbers have no common factors other than 1?
A: If the numbers are relatively prime (meaning their GCD is 1), then their LCM is simply the product of the numbers.
Q: Is there a formula for calculating the LCM of more than two numbers?
A: There isn't a single, concise formula like there is for two numbers using the GCD. The most efficient approach for more than two numbers is usually prime factorization. You find the prime factorization of each number, then take the highest power of each prime factor present and multiply them together.
Q: How do I calculate the LCM for very large numbers?
A: For very large numbers, computational algorithms and specialized software become necessary. The prime factorization method, while conceptually straightforward, becomes computationally intensive for extremely large numbers due to the difficulty of finding prime factors quickly.
Conclusion
Calculating the LCM, while seemingly simple for small numbers, is a fundamental concept with significant implications across various mathematical fields and real-world applications. Mastering the different methods—listing multiples, prime factorization, and the iterative GCD approach—provides a versatile toolkit for tackling a wide range of problems. Understanding the LCM enhances your problem-solving skills and provides a deeper appreciation of the interconnectedness of mathematical concepts. Remember, the choice of method depends on the context and the size of the numbers involved, with prime factorization often being the most efficient and generalizable method for larger numbers. By understanding these principles and applying these methods, you will be well-equipped to handle LCM calculations confidently and effectively.
Latest Posts
Latest Posts
-
What Is 25 Of 14000
Sep 14, 2025
-
Hcf Of 12 And 15
Sep 14, 2025
-
2 1 3 In Decimal
Sep 14, 2025
-
What Is Equal To 4 4
Sep 14, 2025
-
All The Multiples Of Three
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 12 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.