125 Percent As A Fraction
saludintensiva
Sep 14, 2025 · 5 min read
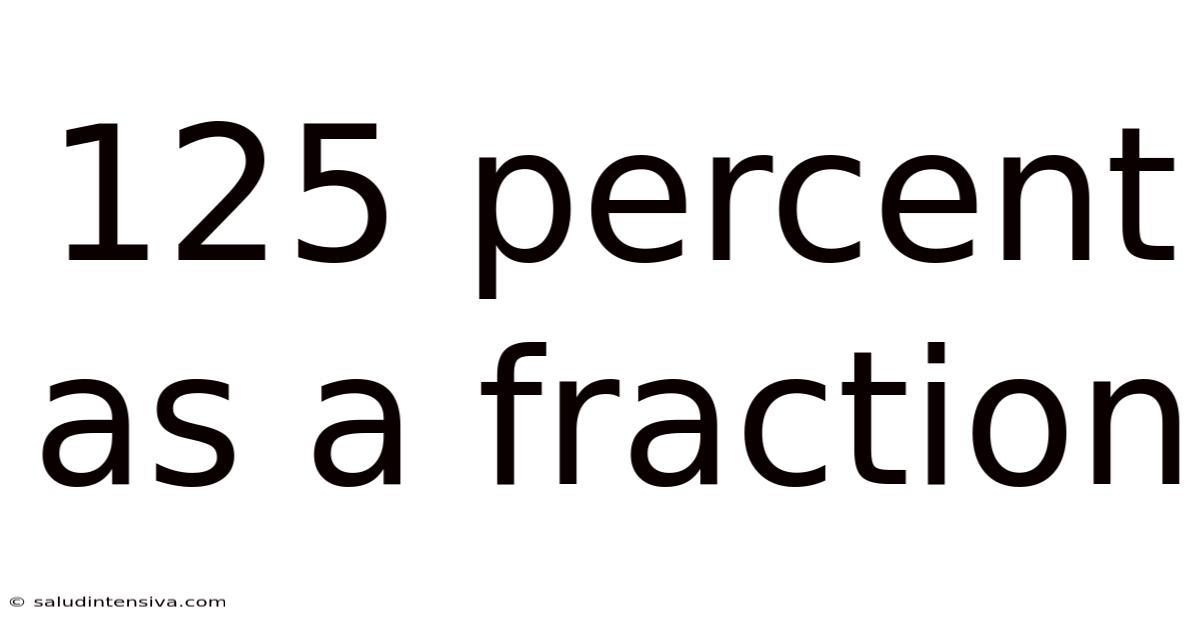
Table of Contents
125 Percent as a Fraction: A Comprehensive Guide
Understanding percentages and their fractional equivalents is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday calculations. This comprehensive guide delves into the conversion of 125 percent to a fraction, exploring the process step-by-step, providing explanations, and addressing common questions. We’ll explore not just the basic conversion, but also the simplification of the resulting fraction and its practical applications. By the end, you’ll possess a solid understanding of how to handle similar percentage-to-fraction conversions.
Understanding Percentages
Before we dive into converting 125 percent to a fraction, let's briefly recap what percentages represent. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 100% represents the whole, or the entirety of something. Any percentage above 100% signifies a value greater than the whole.
Converting 125% to a Fraction: A Step-by-Step Guide
The conversion of 125% to a fraction involves a straightforward process:
-
Write the percentage as a fraction with a denominator of 100: 125% can be written as 125/100. This directly reflects the definition of percentage – a part out of 100.
-
Simplify the fraction: The fraction 125/100 is not in its simplest form. Both the numerator (125) and the denominator (100) are divisible by 25. Dividing both by 25, we get:
125 ÷ 25 = 5 100 ÷ 25 = 4
Therefore, the simplified fraction is 5/4.
-
Express as a mixed number (optional): While 5/4 is a perfectly acceptable answer, it's an improper fraction (the numerator is larger than the denominator). We can convert it to a mixed number, which combines a whole number and a proper fraction. To do this, divide the numerator (5) by the denominator (4):
5 ÷ 4 = 1 with a remainder of 1.
This means 5/4 is equivalent to 1 and 1/4.
Therefore, 125% as a fraction can be expressed as 5/4 or 1 1/4. Both are correct, and the choice depends on the context of the problem.
The Significance of Simplification
Simplifying fractions is crucial for several reasons:
-
Clarity: Simplified fractions are easier to understand and interpret. 5/4 is more concise and easily grasped than 125/100.
-
Calculations: Simplified fractions make subsequent calculations significantly simpler. Imagine needing to multiply or divide with the fraction; working with 5/4 is far more efficient than 125/100.
-
Standardization: In mathematics, presenting answers in their simplest form is a standard practice, ensuring consistency and clarity in communication.
Visualizing 125%
Imagine you have a pizza. 100% of the pizza represents the whole pizza. 125% means you have more than a whole pizza; you have one whole pizza and an additional 25%, or one-quarter (1/4), of another pizza. This visual representation helps to solidify the understanding of 125% as 1 1/4.
Practical Applications of 125%
Understanding the conversion of percentages to fractions has numerous real-world applications:
-
Finance: Calculating interest rates, profit margins, and percentage increases or decreases often involves working with fractions. For example, a 125% increase in investment would mean the investment value has more than doubled.
-
Sales and Discounts: Determining the final price after a percentage discount or markup requires converting percentages to fractions for accurate calculations. A 25% discount on a $100 item would represent (100 - 25)/100 = 75/100 or 3/4 of the original price ($75).
-
Data Analysis: In statistics and data analysis, representing data as fractions often provides a clearer and more concise representation of proportions.
-
Recipe Scaling: If a recipe calls for a certain amount of an ingredient, and you want to increase the yield by 25%, you can use 5/4 to calculate the adjusted amounts.
-
Geometry: Percentages and fractions are crucial in calculating areas, volumes, and other geometric properties.
Further Exploration: Converting Other Percentages to Fractions
The method demonstrated for 125% can be applied to converting any percentage to a fraction. Follow these steps:
-
Write the percentage as a fraction over 100.
-
Simplify the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD.
-
Convert the improper fraction to a mixed number (if applicable).
For example:
- 75% = 75/100 = 3/4
- 200% = 200/100 = 2
- 150% = 150/100 = 3/2 = 1 1/2
- 30% = 30/100 = 3/10
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand, use in calculations, and ensures consistency in mathematical presentations.
Q2: Can I leave 125/100 as the answer?
A2: While technically correct, it’s not the preferred or standardized answer. Simplifying to 5/4 or 1 1/4 is considered best practice.
Q3: What if the percentage is a decimal?
A3: If you have a decimal percentage (e.g., 125.5%), you can convert it to a fraction by first writing it as 125.5/100. Then, multiply both the numerator and the denominator by 10 to remove the decimal, resulting in 1255/1000. Simplify this fraction to its lowest terms.
Q4: Are there any online tools or calculators that can help with this?
A4: Yes, numerous online calculators can convert percentages to fractions. However, understanding the underlying process is crucial for developing a strong mathematical foundation.
Conclusion
Converting 125% to a fraction is a straightforward process that involves writing the percentage as a fraction over 100 and then simplifying the fraction. Understanding this process is crucial for various applications in mathematics and everyday life. The ability to work comfortably with percentages and fractions is a valuable skill that enhances problem-solving abilities across numerous disciplines. Remember to always simplify your fractions to their lowest terms for clarity and efficiency. The equivalent fractions 5/4 and 1 1/4 provide different, yet equally valid, representations of 125%. The best choice depends on the specific context and desired form of the answer.
Latest Posts
Latest Posts
-
14 20 As A Percent
Sep 14, 2025
-
What Is 80 Of 5
Sep 14, 2025
-
What Percent Is 15 20
Sep 14, 2025
-
What Percentage Is 1 4
Sep 14, 2025
-
3 To The 6th Power
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 125 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.