What Is 80 Of $5
saludintensiva
Sep 14, 2025 · 5 min read
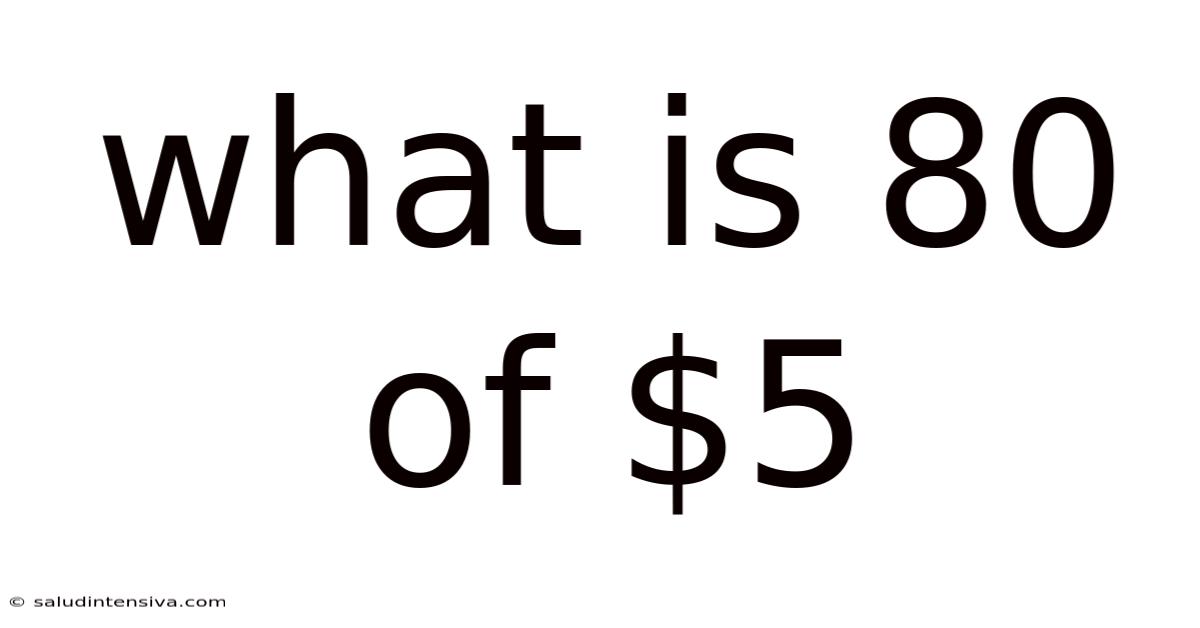
Table of Contents
What is 80% of $5? A Comprehensive Guide to Percentages and Their Applications
Understanding percentages is a fundamental skill in everyday life, from calculating discounts and sales tax to understanding financial reports and statistics. This article will comprehensively explain how to calculate 80% of $5, explore the underlying mathematical concepts, and provide practical applications to help you master percentage calculations. We'll also delve into different methods, address common misconceptions, and offer tips for quick calculations.
Introduction: Understanding Percentages
A percentage is a fraction expressed as a number out of 100. The symbol % represents "per cent," meaning "out of one hundred." So, 80% means 80 out of 100, or 80/100. Calculating a percentage of a number involves finding that fractional part of the number. In our case, we need to find 80% of $5.
Method 1: Using Decimal Conversion
This is arguably the most straightforward method. To calculate 80% of $5, we first convert the percentage to a decimal. We do this by dividing the percentage by 100:
80% ÷ 100 = 0.80 or simply 0.8
Now, we multiply this decimal by the original amount:
0.8 x $5 = $4
Therefore, 80% of $5 is $\boxed{$4}$.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 80% can be written as 80/100, which simplifies to 4/5. Then, we multiply this fraction by the original amount:
(4/5) x $5 = $4
This method demonstrates the underlying fractional nature of percentages. Notice how the 5 in the denominator cancels out with the $5, simplifying the calculation.
Method 3: Proportion Method
The proportion method involves setting up a proportion to solve for the unknown value. We can represent the problem as:
80/100 = x/$5
To solve for x (which represents 80% of $5), we cross-multiply:
100x = 80 x $5
100x = $400
x = $400 / 100
x = $4
This method is particularly helpful when dealing with more complex percentage problems.
Explanation with Scientific Background
The core mathematical concept behind percentage calculations is the concept of ratio and proportion. A percentage represents a ratio of a part to a whole, where the whole is always considered 100%. The proportion method directly applies this concept, expressing the relationship between the percentage and the part as equivalent to the relationship between 100% and the whole.
Furthermore, the decimal conversion method is a direct application of the distributive property of multiplication. When we multiply 0.8 by $5, we are essentially distributing the fraction 80/100 across the value of $5.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-life situations:
- Shopping: Calculating discounts, sales tax, and final prices. For example, if a $20 item is discounted by 20%, you can use these methods to determine the final price.
- Finance: Determining interest rates, loan repayments, and investment returns. Understanding percentage changes in investment values is essential for financial planning.
- Statistics: Analyzing data sets, interpreting graphs and charts, and understanding statistical significance. Percentages are fundamental to expressing and comparing data.
- Science: Expressing concentrations of solutions, calculating experimental yields, and analyzing experimental errors. Many scientific concepts rely on accurate percentage calculations.
- Everyday Life: Tips and gratuities in restaurants, calculating the percentage of a task completed, and comparing different options based on cost and value.
Common Misconceptions about Percentages
- Adding percentages directly: You cannot simply add percentages unless they are of the same base value. For example, a 10% increase followed by a 10% decrease does not result in a net change of 0%.
- Confusing percentage change with percentage points: A change from 10% to 20% is a 10 percentage point increase, but a 100% increase in the percentage itself. This distinction is crucial for clear communication.
- Incorrect decimal conversion: A common error is incorrectly converting percentages to decimals. Always remember to divide the percentage by 100.
Tips for Quick Percentage Calculations
- Memorize common percentages: Knowing the decimal equivalents of common percentages (e.g., 10%, 25%, 50%) can speed up calculations.
- Use mental math: For simple percentages, try using mental math techniques to avoid the need for a calculator.
- Break down complex percentages: A complex percentage, such as 17%, can be broken down into simpler percentages (10% + 5% + 2%) for easier calculation.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate x% of y?
- A: Convert x% to a decimal by dividing by 100 (x/100). Then, multiply the decimal by y.
-
Q: What is the difference between percentage increase and percentage decrease?
- A: A percentage increase calculates the increase relative to the original value, while a percentage decrease calculates the decrease relative to the original value.
-
Q: How can I calculate the percentage of one number compared to another?
- A: Divide the first number by the second number and multiply the result by 100. This gives the percentage of the first number relative to the second.
-
Q: Are there any online calculators for percentage calculations?
- A: While there are numerous online percentage calculators available, understanding the underlying methodology is vital for applying these concepts effectively in different contexts.
Conclusion: Mastering Percentage Calculations
Calculating 80% of $5, as we’ve seen, is a relatively straightforward task. However, the broader understanding of percentage calculations extends far beyond this specific example. Mastering these calculations equips you with a powerful tool applicable across diverse fields, from everyday finances to complex scientific analyses. By understanding the different methods, addressing common misconceptions, and utilizing helpful tips, you can confidently tackle any percentage-related problem. The key is to grasp the fundamental mathematical principles underlying these calculations and apply them strategically to solve a wide range of problems. Remember to practice regularly to solidify your understanding and build confidence in your abilities.
Latest Posts
Latest Posts
-
2 3 4 Divided By 3
Sep 14, 2025
-
What Percentage Is 15 20
Sep 14, 2025
-
Convert Mm To Sq Feet
Sep 14, 2025
-
Rounding To The Nearest 5
Sep 14, 2025
-
How Long Is 510 Minutes
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of $5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.