What Percentage Is 15 20
saludintensiva
Sep 14, 2025 · 5 min read
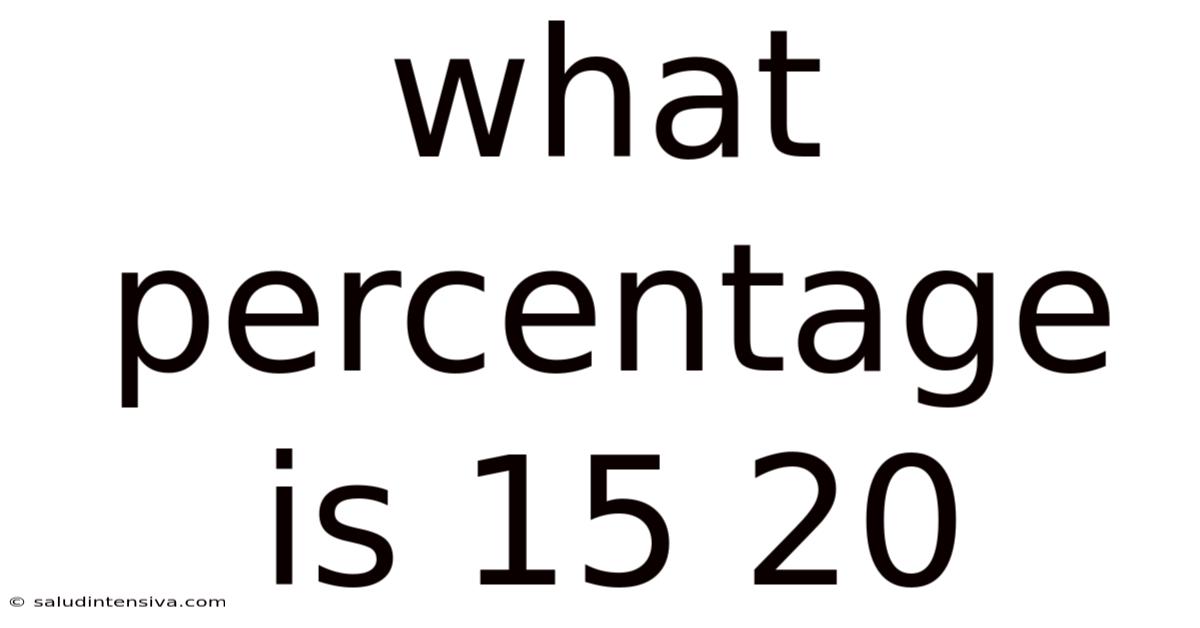
Table of Contents
What Percentage is 15 of 20? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will delve into the question, "What percentage is 15 of 20?", providing a detailed explanation of the calculation, exploring different methods, and offering valuable insights into related percentage problems. We'll also examine the broader context of percentage calculations and their importance in various fields.
Understanding Percentages: A Quick Recap
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are a convenient way to express proportions and compare different quantities.
Calculating "What Percentage is 15 of 20?"
There are several ways to calculate what percentage 15 represents of 20. Let's explore the most common methods:
Method 1: Using the Basic Percentage Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 15
- Whole: 20
Substituting these values into the formula:
(15 / 20) x 100% = 0.75 x 100% = 75%
Therefore, 15 is 75% of 20.
Method 2: Using Proportions
We can also solve this using proportions. We set up a proportion where x represents the unknown percentage:
15/20 = x/100
To solve for x, we cross-multiply:
20x = 1500
x = 1500 / 20
x = 75
Therefore, 15 is 75% of 20.
Method 3: Simplifying the Fraction
Before multiplying by 100%, we can simplify the fraction 15/20:
15/20 = 3/4
Now, we convert the fraction 3/4 to a percentage:
(3/4) x 100% = 0.75 x 100% = 75%
This method highlights the importance of simplifying fractions to make calculations easier.
Beyond the Calculation: Understanding the Context
While the calculation itself is straightforward, understanding the context is crucial. The statement "15 is 75% of 20" implies a relationship between two quantities. Imagine, for example, that you had 20 apples, and you gave away 15. You would have given away 75% of your apples.
Applications of Percentage Calculations in Real-Life Scenarios:
Percentage calculations are ubiquitous in daily life and various professional fields. Here are a few examples:
- Retail Sales: Calculating discounts (e.g., a 20% discount on a $100 item), sales tax, and profit margins.
- Finance: Determining interest rates, loan repayments, and investment returns. Understanding percentage change is crucial for tracking the performance of investments.
- Science and Statistics: Expressing data as percentages helps in visualizing and interpreting results, such as in surveys, scientific experiments, and demographic studies. For instance, expressing survey results as percentages makes it easy to compare different responses.
- Education: Grading systems often rely on percentages to represent a student's performance. Calculating the percentage score on an exam is a common practice.
- Everyday Life: Many everyday situations involve percentages. Examples include calculating tips in restaurants, determining the percentage of completion of a project, and understanding nutritional information on food labels.
Common Percentage-Related Problems and How to Solve Them
Beyond the basic calculation, there are several variations of percentage problems. Let's explore a few:
- Finding the Percentage Increase or Decrease: This involves calculating the change in a value as a percentage of the original value. The formula is:
[(New Value - Old Value) / Old Value] x 100%
For example, if a price increases from $10 to $15, the percentage increase is:
[(15 - 10) / 10] x 100% = 50%
- Finding a Percentage of a Number: This involves calculating a specific percentage of a given number. The formula is:
(Percentage / 100) x Number
For example, finding 25% of 80:
(25/100) x 80 = 20
- Finding the Original Value: This involves determining the original value when given a percentage and the resulting value. This often requires working backward from the percentage calculation.
For example, if 75% of a number is 15, then the original number is:
15 / (75/100) = 20
Frequently Asked Questions (FAQ)
- What is the difference between percentage and proportion? A proportion is a ratio of two quantities, while a percentage is a specific type of proportion expressed as a number out of 100.
- How do I convert a decimal to a percentage? Multiply the decimal by 100 and add the % symbol. For example, 0.75 becomes 75%.
- How do I convert a fraction to a percentage? Convert the fraction to a decimal by dividing the numerator by the denominator, and then multiply the decimal by 100 and add the % symbol.
- What are some common percentage mistakes to avoid? Common mistakes include incorrect placement of the decimal point, using the wrong formula, and forgetting to multiply by 100% when converting a decimal or fraction to a percentage.
Conclusion:
Understanding percentages is an essential skill with far-reaching applications. The calculation of "what percentage is 15 of 20?"—which equals 75%—serves as a fundamental example. Mastering various methods for calculating percentages and understanding their application in different scenarios will enhance your problem-solving abilities and empower you to confidently tackle various challenges in your personal and professional life. From analyzing financial data to understanding scientific results, the ability to work with percentages is a valuable asset in numerous contexts. Remember to practice regularly and focus on understanding the underlying concepts to build a solid foundation in this critical area of mathematics. This comprehensive understanding of percentage calculations will not only help you answer specific questions but also equip you with the skills to tackle a wider range of quantitative problems efficiently and accurately.
Latest Posts
Latest Posts
-
How To Get Common Factor
Sep 14, 2025
-
Whats Bigger 3 8 Or 7 16
Sep 14, 2025
-
Lcm Of 32 And 40
Sep 14, 2025
-
Lcm Of 17 And 13
Sep 14, 2025
-
1 3 To The 4th Power
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 15 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.