Lcm Of 17 And 13
saludintensiva
Sep 14, 2025 · 5 min read
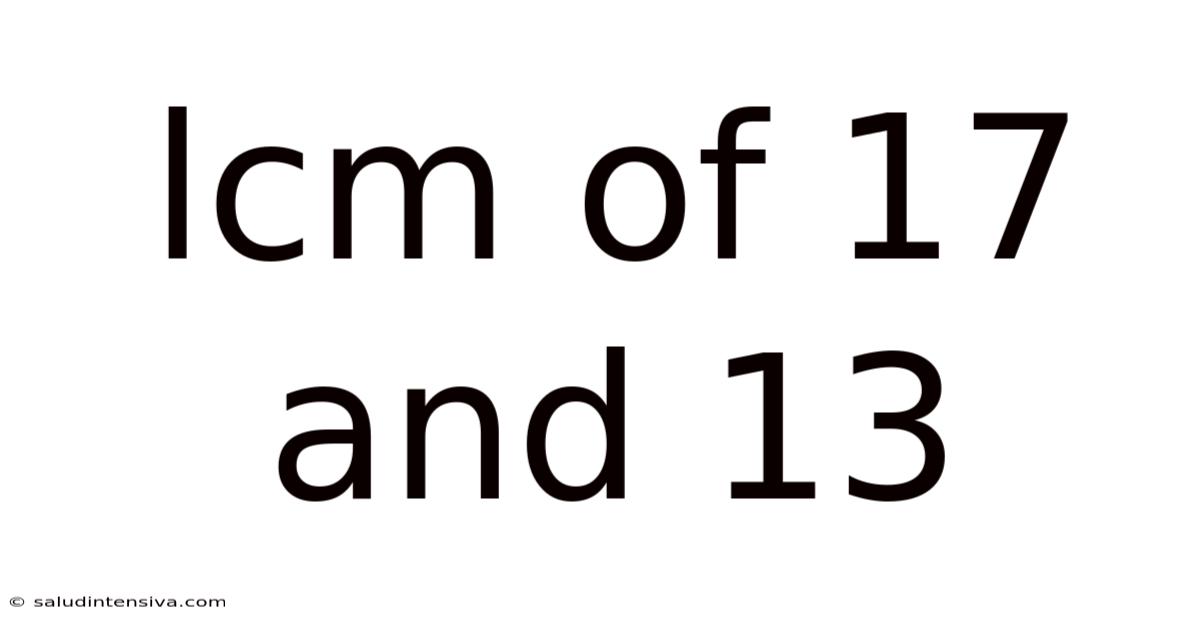
Table of Contents
Finding the Least Common Multiple (LCM) of 17 and 13: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation is crucial for a strong foundation in mathematics. This comprehensive guide delves into the LCM of 17 and 13, exploring various approaches, explaining the reasoning behind each step, and providing a deeper understanding of this fundamental mathematical concept. This article will equip you with the skills to calculate the LCM of any two numbers, not just 17 and 13.
Understanding Least Common Multiple (LCM)
Before diving into the calculation for the specific numbers 17 and 13, let's establish a clear understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. This concept is fundamental in various mathematical operations, including simplifying fractions, solving equations, and working with rhythmic patterns.
Method 1: Prime Factorization Method
This method is considered the most fundamental and widely applicable approach for finding the LCM. It involves breaking down each number into its prime factors. A prime factor is a number that is only divisible by 1 and itself (e.g., 2, 3, 5, 7, 11, etc.).
-
Prime Factorization of 17: 17 is a prime number itself. Therefore, its prime factorization is simply 17.
-
Prime Factorization of 13: Similar to 17, 13 is also a prime number. Its prime factorization is 13.
-
Finding the LCM: Since both 17 and 13 are prime numbers and have no common factors other than 1, their least common multiple is simply the product of the two numbers.
Therefore: LCM(17, 13) = 17 * 13 = 221
Method 2: Listing Multiples Method
This method is more intuitive but can be less efficient for larger numbers. It involves listing the multiples of each number until you find the smallest multiple that is common to both.
-
Multiples of 17: 17, 34, 51, 68, 85, 102, 119, 136, 153, 170, 187, 204, 221, ...
-
Multiples of 13: 13, 26, 39, 52, 65, 78, 91, 104, 117, 130, 143, 156, 169, 182, 195, 208, 221,...
-
Finding the LCM: By comparing the lists, we observe that the smallest common multiple of 17 and 13 is 221.
This method demonstrates the concept clearly but becomes cumbersome when dealing with larger numbers or numbers with many factors.
Method 3: Using the Greatest Common Divisor (GCD)
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. There's a useful formula connecting LCM and GCD:
LCM(a, b) * GCD(a, b) = a * b
Where 'a' and 'b' are the two numbers.
-
Finding the GCD of 17 and 13: Since both 17 and 13 are prime numbers and have no common factors other than 1, their GCD is 1.
-
Applying the formula:
LCM(17, 13) * GCD(17, 13) = 17 * 13 LCM(17, 13) * 1 = 221 LCM(17, 13) = 221
Why is Understanding LCM Important?
The concept of LCM extends far beyond simple arithmetic exercises. It plays a vital role in various applications, including:
-
Fraction Arithmetic: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/17 and 1/13, we would find the LCM (221) and rewrite the fractions with this common denominator.
-
Scheduling and Time Management: LCM helps determine when events with different periodicities will occur simultaneously. For example, if two machines operate at different intervals (one every 17 minutes and the other every 13 minutes), the LCM will tell you when they'll both operate at the same time.
-
Music Theory: LCM is used to find the least common denominator in musical rhythms and note durations.
Further Exploration: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then take the highest power of each prime factor present in any of the factorizations. For the listing multiples method, the process becomes significantly more complex and less efficient. The GCD method can also be extended using a more generalized approach involving multiple GCDs.
Frequently Asked Questions (FAQ)
Q1: Is the LCM always greater than the two numbers?
A1: Generally, yes, unless one of the numbers is a factor of the other. For instance, the LCM of 4 and 8 is 8 (8 is a multiple of 4). However, in most cases involving two relatively prime numbers (like 17 and 13, which share no common factors other than 1), the LCM will be larger than both numbers.
Q2: Can I use a calculator to find the LCM?
A2: Yes, many scientific calculators and online calculators have built-in functions to calculate the LCM of two or more numbers. However, understanding the underlying methods is crucial for grasping the mathematical concept.
Q3: What if the numbers are very large?
A3: For extremely large numbers, the prime factorization method might become computationally intensive. In such scenarios, more advanced algorithms and computational tools are employed.
Conclusion
Finding the LCM of 17 and 13, which equals 221, demonstrates a fundamental concept in mathematics with far-reaching applications. While the simplicity of this specific example allows for easy calculation using multiple methods, the underlying principles remain essential for tackling more complex scenarios involving larger numbers or multiple numbers. Mastering the LCM calculation reinforces your understanding of prime factorization, divisibility, and the interconnectedness of mathematical concepts. By understanding these methods and their applications, you build a stronger mathematical foundation and develop valuable problem-solving skills applicable across various disciplines.
Latest Posts
Latest Posts
-
60 Minutes In 1 Hour
Sep 14, 2025
-
1 2 3 Or 4
Sep 14, 2025
-
How Many Inches Is 18cm
Sep 14, 2025
-
Is 2 3 Larger Than 3 4
Sep 14, 2025
-
4 Out Of 5 Percent
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 17 And 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.