Is 2/3 Larger Than 3/4
saludintensiva
Sep 14, 2025 · 5 min read
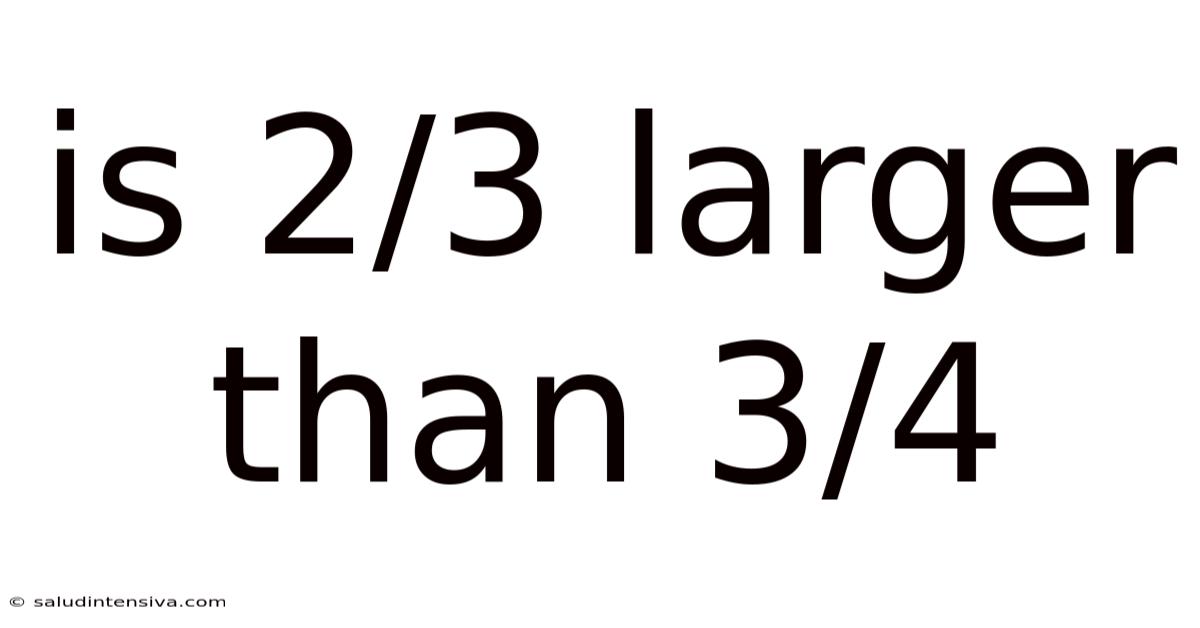
Table of Contents
Is 2/3 Larger Than 3/4? Deconstructing Fractions and Understanding Comparisons
This article will delve into the seemingly simple question: Is 2/3 larger than 3/4? While the answer might seem immediately apparent to some, a deeper understanding of fraction comparison is crucial for developing strong mathematical foundations. We'll explore various methods for comparing fractions, providing a clear and comprehensive explanation suitable for learners of all levels. This includes understanding the concept of fractions, different comparison techniques, and applications of this knowledge in real-world scenarios.
Understanding Fractions: A Quick Recap
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/3, the numerator is 2 and the denominator is 3, meaning we have 2 out of 3 equal parts.
Method 1: Finding a Common Denominator
This is arguably the most common and straightforward method for comparing fractions. The principle is simple: to compare fractions with different denominators, we need to rewrite them with a common denominator. A common denominator is a number that is a multiple of both denominators.
Let's apply this to our problem: Is 2/3 larger than 3/4?
-
Find a common denominator: The denominators are 3 and 4. The least common multiple (LCM) of 3 and 4 is 12. This means we'll rewrite both fractions with a denominator of 12.
-
Rewrite the fractions:
-
To change 2/3 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
To change 3/4 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 3: (3 x 3) / (4 x 3) = 9/12
-
-
Compare the new fractions: Now we have 8/12 and 9/12. Since 8 is less than 9, we conclude that 8/12 is smaller than 9/12.
-
Conclusion: Therefore, 2/3 is smaller than 3/4.
Method 2: Converting to Decimals
Another effective method for comparing fractions involves converting them to decimals. This approach is particularly useful when dealing with fractions that are difficult to express with a common denominator.
To convert a fraction to a decimal, we simply divide the numerator by the denominator.
-
Convert 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667 (repeating decimal)
-
Convert 3/4 to a decimal: 3 ÷ 4 = 0.75
-
Compare the decimals: Since 0.6667 is less than 0.75, we confirm that 2/3 is smaller than 3/4.
Method 3: Visual Representation
Visual aids can be incredibly helpful in understanding fraction comparisons, especially for visual learners. Imagine two identical circles.
-
Representing 2/3: Divide the first circle into three equal parts and shade two of them.
-
Representing 3/4: Divide the second circle into four equal parts and shade three of them.
By visually comparing the shaded areas, it becomes evident that the shaded portion of the circle representing 3/4 is larger than the shaded portion representing 2/3. This visual comparison reinforces the conclusion that 2/3 is smaller than 3/4.
Method 4: Cross-Multiplication
Cross-multiplication provides a quick and efficient way to compare two fractions. This method involves multiplying the numerator of one fraction by the denominator of the other, and vice versa. The larger product corresponds to the larger fraction.
-
Cross-multiply:
-
Multiply the numerator of 2/3 (2) by the denominator of 3/4 (4): 2 x 4 = 8
-
Multiply the numerator of 3/4 (3) by the denominator of 2/3 (3): 3 x 3 = 9
-
-
Compare the products: Since 8 < 9, we conclude that 2/3 < 3/4.
Understanding the Differences: Why It Matters
The seemingly small difference between 2/3 and 3/4 highlights the importance of precise calculations and accurate comparisons in various fields. In fields like engineering, construction, and even baking, a slight miscalculation in proportions can lead to significant errors or undesirable outcomes. Understanding fraction comparison is fundamental to ensuring accuracy and precision.
Real-World Applications: Beyond the Classroom
The ability to compare fractions extends far beyond the classroom. Consider these examples:
-
Cooking and Baking: Recipes often call for fractional measurements of ingredients. Understanding fraction comparison ensures accurate ingredient proportions and successful results.
-
Construction and Engineering: Precise measurements are crucial in these fields. Comparing fractions helps ensure the accuracy of dimensions and calculations.
-
Finance and Budgeting: Managing finances often involves working with fractions and percentages. Comparing fractions helps in understanding proportions of savings, expenses, and investments.
-
Data Analysis: In analyzing data, understanding fractions and their relationships is crucial for interpreting proportions and trends within datasets.
Frequently Asked Questions (FAQs)
Q: Are there other methods to compare fractions?
A: Yes, other methods exist, particularly for more complex fractions. These might involve simplifying fractions before comparison or using number lines to visualize the relative positions of the fractions.
Q: What if the fractions have the same denominator?
A: If fractions have the same denominator, simply compare their numerators. The fraction with the larger numerator is the larger fraction.
Q: Can I use a calculator to compare fractions?
A: While a calculator can convert fractions to decimals, it's beneficial to understand the underlying mathematical principles involved in comparing fractions.
Conclusion: Mastering Fraction Comparisons
This comprehensive exploration of comparing fractions clarifies the method for determining whether 2/3 is larger than 3/4. Through various methods – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – we definitively established that 2/3 is smaller than 3/4. However, the true value of this exercise lies not just in the answer itself, but in the development of a deeper understanding of fraction manipulation and comparison techniques. This fundamental skill serves as a cornerstone for more advanced mathematical concepts and has practical applications across numerous fields. Mastering fraction comparison equips you with a crucial tool for problem-solving and critical thinking in various aspects of life.
Latest Posts
Latest Posts
-
Lcm For 4 And 8
Sep 14, 2025
-
Mixed Number Minus Whole Number
Sep 14, 2025
-
Whats Half Of 1 1 2
Sep 14, 2025
-
Gcf For 8 And 20
Sep 14, 2025
-
Random Number 1 50
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Larger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.