Whats Half Of 1 1/2
saludintensiva
Sep 14, 2025 · 6 min read
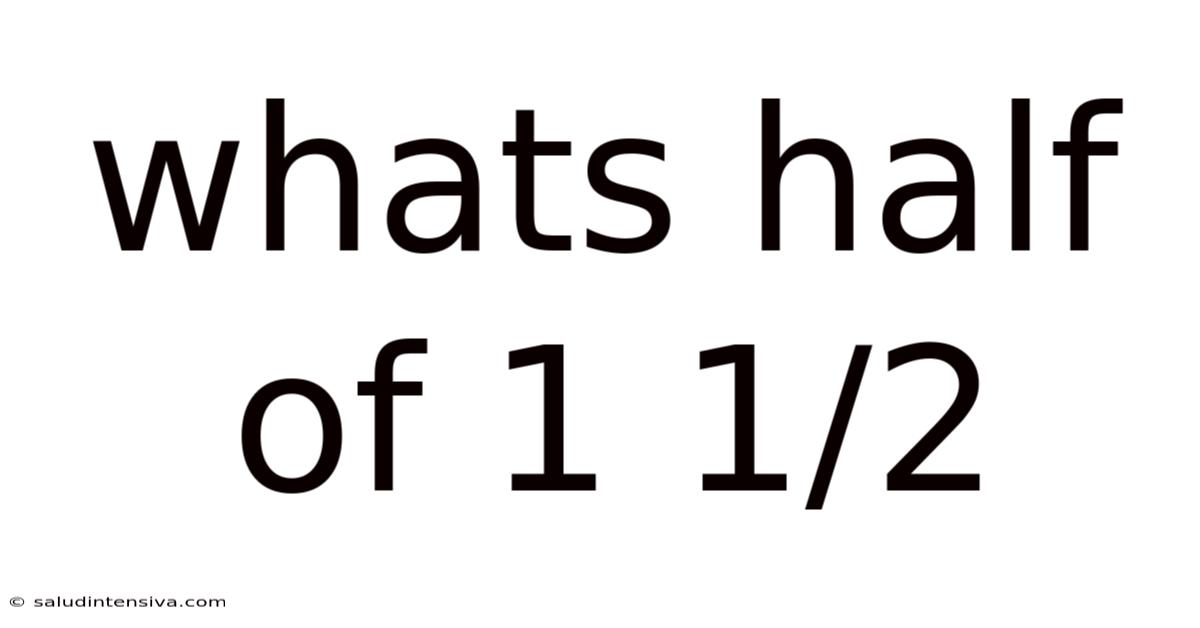
Table of Contents
What's Half of 1 1/2? A Deep Dive into Fractions and Division
Finding half of 1 1/2 might seem like a simple task, suitable only for elementary school. However, understanding the underlying principles involved offers a valuable opportunity to solidify our grasp of fractions, mixed numbers, and division – concepts fundamental to mathematics and applicable across numerous fields. This article will not only answer the question "What's half of 1 1/2?" but will also delve into the various methods for solving this problem, exploring the underlying mathematical concepts and extending our understanding to more complex scenarios.
Understanding Fractions and Mixed Numbers
Before tackling the problem, let's refresh our understanding of key terms. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1 and the denominator is 2, indicating one out of two equal parts.
A mixed number combines a whole number and a fraction. For instance, 1 1/2 represents one whole unit and one-half of another unit. To work effectively with mixed numbers in calculations, it's often helpful to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator. To convert 1 1/2 to an improper fraction, we multiply the whole number (1) by the denominator (2), add the numerator (1), and keep the same denominator. This gives us (1 x 2) + 1 / 2 = 3/2.
Method 1: Converting to an Improper Fraction and Dividing
This is arguably the most straightforward method. We start by converting the mixed number 1 1/2 into an improper fraction, as explained above: 3/2. Finding half of a number is the same as dividing it by 2. So, we need to divide 3/2 by 2. Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction. The reciprocal of 2 (or 2/1) is 1/2.
Therefore, the calculation becomes: (3/2) ÷ 2 = (3/2) x (1/2) = 3/4.
Therefore, half of 1 1/2 is 3/4.
Method 2: Finding Half of Each Part Separately
We can also approach this problem by considering the whole number and the fraction separately. 1 1/2 can be thought of as 1 + 1/2. Finding half of this is the same as finding half of 1 and half of 1/2 and adding the results together.
Half of 1 is 1/2.
Half of 1/2 is (1/2) ÷ 2 = (1/2) x (1/2) = 1/4.
Adding these together: 1/2 + 1/4 = 2/4 + 1/4 = 3/4.
Again, we arrive at the answer: 3/4.
Method 3: Visual Representation
A visual approach can be incredibly helpful, especially for those who prefer a more concrete understanding. Imagine a circle representing one whole unit. Divide this circle in half. Now, consider another half-circle, representing the 1/2 in 1 1/2. You now have a total of one and a half circles. To find half of this, divide each of the three half-circles in half again. You'll end up with three quarter-circles, which represent 3/4. This visual method provides a strong intuitive grasp of the concept.
Extending the Concept: Halving Other Mixed Numbers
The methods described above can be applied to find half of any mixed number. Let's consider another example: finding half of 2 2/3.
Step 1: Convert to an improper fraction:
2 2/3 = (2 x 3) + 2 / 3 = 8/3
Step 2: Divide by 2:
(8/3) ÷ 2 = (8/3) x (1/2) = 8/6 = 4/3
Step 3: Convert back to a mixed number (optional):
4/3 = 1 1/3
Therefore, half of 2 2/3 is 4/3 or 1 1/3.
The Importance of Understanding Fractions in Everyday Life
While the concept of finding half of 1 1/2 might seem trivial, mastering fraction manipulation is crucial for everyday life. From cooking (following recipes that call for fractional amounts of ingredients) to budgeting (understanding proportions and percentages) to construction (measuring and cutting materials), fractions are essential tools. A strong grasp of fractions empowers us to make accurate calculations and solve practical problems confidently.
Practical Applications and Real-World Examples
- Cooking: A recipe calls for 1 1/2 cups of flour. To halve the recipe, you'd need 3/4 cup of flour.
- Sewing: A pattern requires 1 1/2 yards of fabric. To make a smaller version, you'd need 3/4 of a yard.
- Construction: A project needs 1 1/2 gallons of paint. To estimate paint needs for a smaller area, you'd need 3/4 of a gallon.
- Finance: If you need to split a bill of 1 1/2 times the normal amount, each person should pay 3/4 of the original cost.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Yes, you can. Most calculators can handle fractions, either by using the fraction function directly or by converting the mixed number to a decimal (1.5) and then dividing by 2 (resulting in 0.75). Remember to convert back to a fraction if needed (0.75 = 3/4).
-
Q: Why is it important to learn different methods for solving this problem? A: Learning multiple methods provides a deeper understanding of the underlying mathematical principles. Each approach highlights different aspects of fraction manipulation and reinforces the interconnectedness of mathematical concepts. Different methods also cater to different learning styles, allowing individuals to grasp the concepts in ways that resonate with them.
-
Q: What if the question asked for a third of 1 1/2? A: The same principles apply. Convert 1 1/2 to 3/2, then divide by 3: (3/2) ÷ 3 = (3/2) x (1/3) = 1/2. Therefore, a third of 1 1/2 is 1/2.
-
Q: Can this be applied to larger numbers? A: Absolutely! The methods discussed work equally well for larger mixed numbers. Simply convert to an improper fraction, divide, and then convert back to a mixed number if required.
Conclusion
Finding half of 1 1/2, while seemingly simple, offers a powerful opportunity to reinforce our understanding of fractions, mixed numbers, and division. By exploring multiple methods – converting to improper fractions, halving each part separately, and using visual representations – we develop a more robust and intuitive grasp of these crucial mathematical concepts. Understanding these principles is not only essential for academic success but also empowers us to tackle practical problems confidently in everyday life. Remember, the key lies in understanding the underlying principles rather than simply memorizing a formula; this will equip you to tackle even more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
Convert 7 To A Decimal
Sep 14, 2025
-
6 5 M 1 26
Sep 14, 2025
-
Whats Equivalent To 2 4
Sep 14, 2025
-
Is 2 5 Greater Than 3 5
Sep 14, 2025
-
How Much Is 108 Minutes
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Whats Half Of 1 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.