13 16 As A Decimal
saludintensiva
Sep 12, 2025 · 5 min read
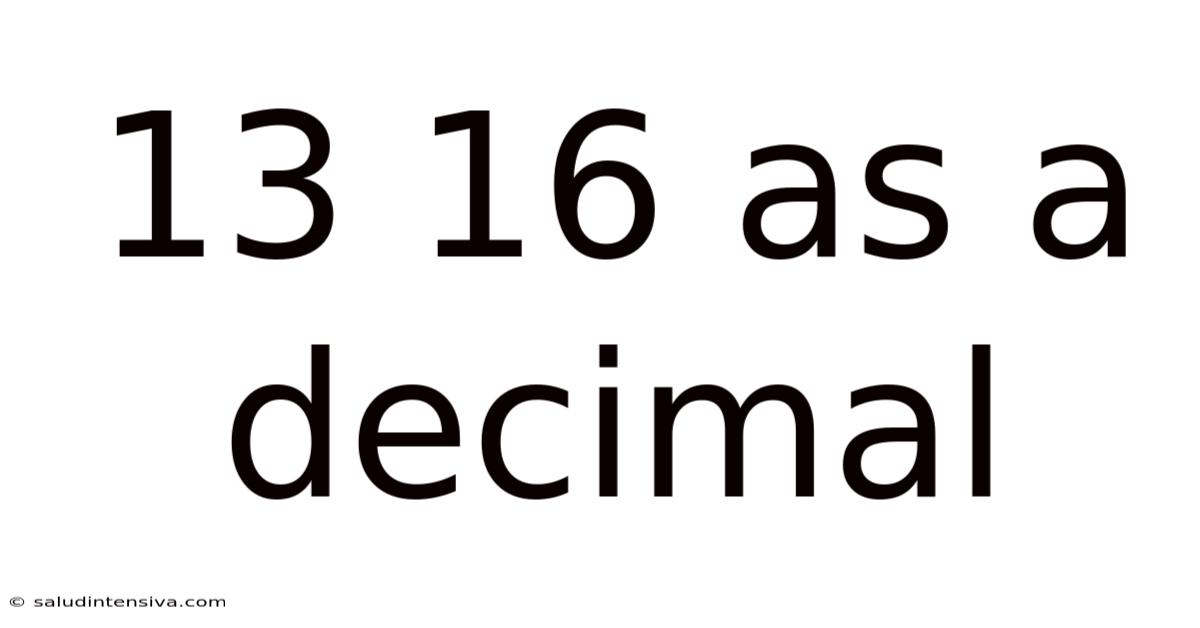
Table of Contents
Decoding 13/16 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This comprehensive guide will delve into the conversion of the fraction 13/16 into its decimal form, exploring various methods and providing a deeper understanding of the underlying principles. We'll cover the basic conversion process, explore different approaches, and address common questions to ensure you grasp this concept thoroughly. This article will be particularly helpful for students learning about fractions and decimals, as well as anyone looking to refresh their math skills.
Introduction: Fractions and Decimals
Before diving into the specific conversion of 13/16, let's briefly review the relationship between fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal is another way to represent a part of a whole, using a base-ten system. The decimal point separates the whole number part from the fractional part. Converting between fractions and decimals is a crucial skill for various mathematical operations and real-world applications.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. In this case, we need to divide the numerator (13) by the denominator (16).
-
Set up the long division: Write 13 as the dividend (inside the division symbol) and 16 as the divisor (outside). Add a decimal point and zeros to the dividend to allow for the division process to continue.
-
Perform the division: Divide 16 into 13.0000... Since 16 doesn't go into 13, you begin by placing a zero above the decimal point. Then, you divide 16 into 130. It goes in 8 times (8 x 16 = 128). Subtract 128 from 130, leaving a remainder of 2.
-
Continue the division: Bring down the next zero (making it 20). 16 goes into 20 once (1 x 16 = 16). Subtract 16 from 20, leaving a remainder of 4.
-
Repeat the process: Bring down another zero (making it 40). 16 goes into 40 twice (2 x 16 = 32). Subtract 32 from 40, leaving a remainder of 8.
-
Continue until you see a pattern or reach desired precision: Bring down another zero (making it 80). 16 goes into 80 five times (5 x 16 = 80). The remainder is 0, meaning the division is complete.
Therefore, 13/16 = 0.8125
Method 2: Converting to a Power of 10 Denominator
This method involves finding an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). While not always possible, it's a valuable technique when it works. Unfortunately, 16 doesn't easily convert to a power of 10. It's a power of 2 (2<sup>4</sup>), and powers of 2 and powers of 5 are needed to create a power of 10. Therefore, this method isn't directly applicable to 13/16. We'd need to utilize the long division method or another approach.
Method 3: Using a Calculator
The simplest way, especially for more complex fractions, is to use a calculator. Simply input 13 ÷ 16, and the calculator will directly provide the decimal equivalent: 0.8125. This method is efficient for quick conversions, but understanding the underlying principles is still crucial for problem-solving and deeper mathematical comprehension.
Understanding the Decimal Value: 0.8125
The decimal 0.8125 represents the value of 13/16. This means that if you divide something into 16 equal parts, 13 of those parts represent 0.8125 of the whole. This decimal value can be further broken down:
- 0.8: Represents eight-tenths.
- 0.01: Represents one-hundredth.
- 0.002: Represents two-thousandths.
- 0.0005: Represents five ten-thousandths.
Adding these together confirms the total value of 0.8125.
Real-World Applications
Understanding the decimal equivalent of fractions is crucial in various everyday situations:
- Measurements: Converting inches to centimeters, or fractions of an inch to decimal inches for precise measurements in construction or engineering.
- Finance: Calculating percentages, interest rates, or proportions of investments.
- Cooking and Baking: Following recipes that utilize fractions and needing to convert them to decimal equivalents for precise measurements.
- Data Analysis: Representing data as proportions or percentages in various charts and graphs.
Frequently Asked Questions (FAQ)
-
Q: Can all fractions be converted to terminating decimals?
- A: No. Fractions with denominators that can be expressed as 2<sup>m</sup>5<sup>n</sup> (where m and n are non-negative integers) will result in terminating decimals. Other fractions will result in repeating decimals (e.g., 1/3 = 0.333...).
-
Q: What if I get a repeating decimal when converting a fraction?
- A: Repeating decimals indicate that the fraction cannot be precisely represented as a terminating decimal. You can either express it as a repeating decimal (e.g., 0.333...) or round it to a certain number of decimal places depending on the required precision.
-
Q: Is there a way to convert decimals back to fractions?
- A: Yes. You can convert a decimal to a fraction by writing the decimal as a fraction over a power of 10 (e.g., 0.8125 = 8125/10000) and then simplifying the fraction to its lowest terms. For 0.8125, simplification would lead back to 13/16.
-
Q: Why is understanding this conversion important?
- A: This conversion is fundamental for various mathematical operations, problem-solving, and real-world applications where both fractions and decimals are used interchangeably. It allows for greater flexibility and efficiency in calculations.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting 13/16 to its decimal equivalent (0.8125) involves a straightforward process, primarily utilizing long division or a calculator. Understanding the underlying principles, however, is crucial for broader mathematical comprehension and application. This guide has provided a comprehensive explanation of the process, explored different methods, and addressed common questions. By mastering this fundamental skill, you enhance your mathematical proficiency and open doors to more advanced concepts and real-world problem-solving. Remember to practice these conversions regularly to build your confidence and solidify your understanding. The ability to seamlessly transition between fractions and decimals is a cornerstone of mathematical literacy and proficiency.
Latest Posts
Latest Posts
-
Year Over Year Percentage Calculator
Sep 12, 2025
-
90 Days From 8 26
Sep 12, 2025
-
Whats 15 Percent Of 65
Sep 12, 2025
-
What Was 26 Weeks Ago
Sep 12, 2025
-
How Long Is 3600 Seconds
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 13 16 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.