Whats 15 Percent Of 65
saludintensiva
Sep 12, 2025 · 5 min read
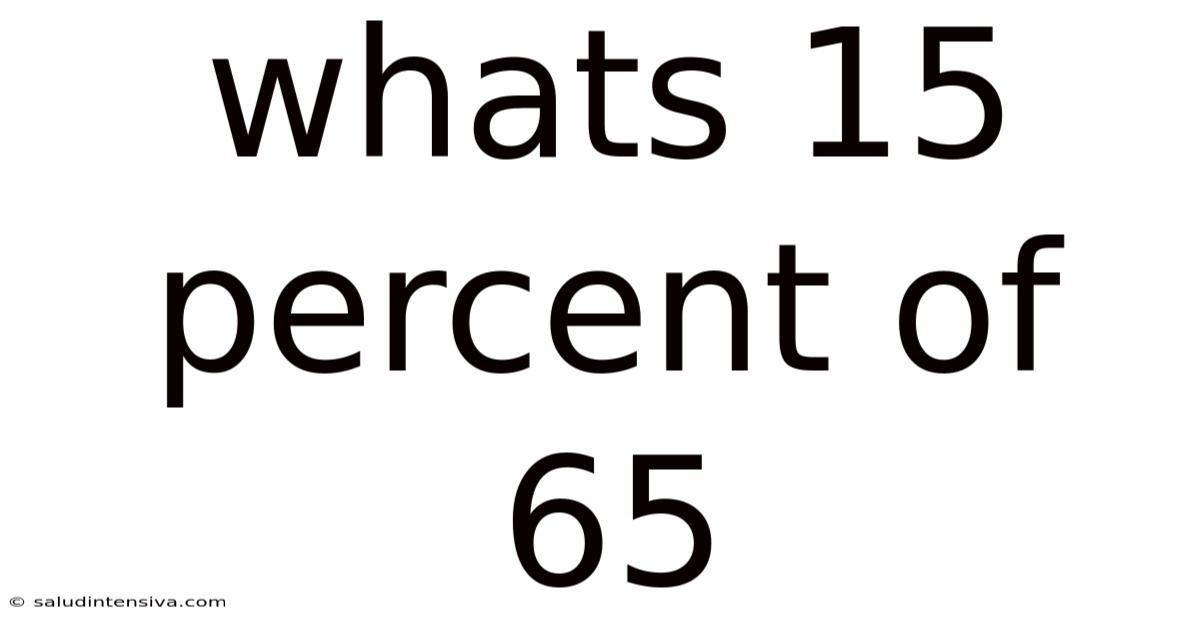
Table of Contents
What's 15 Percent of 65? A Deep Dive into Percentages and Their Applications
Finding 15 percent of 65 might seem like a simple calculation, but understanding the underlying principles of percentages unlocks a powerful tool applicable in numerous real-world scenarios. This article will not only show you how to calculate 15% of 65, but also explore the broader concept of percentages, different calculation methods, and practical applications to solidify your understanding. We'll delve into the mathematics behind it, explore alternative approaches, and even touch upon the importance of percentage calculations in various fields.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 15% means 15 out of 100, or 15/100, which is equivalent to the decimal 0.15. Understanding this fundamental concept is crucial for performing percentage calculations. The question, "What's 15 percent of 65?" is essentially asking: "What is 15/100 of 65?"
Method 1: The Direct Calculation Method
The most straightforward method to calculate 15% of 65 involves converting the percentage to a decimal and then multiplying it by the number.
-
Step 1: Convert the percentage to a decimal: 15% is equivalent to 15/100 = 0.15
-
Step 2: Multiply the decimal by the number: 0.15 * 65 = 9.75
Therefore, 15% of 65 is $\boxed{9.75}$.
Method 2: Using Fractions
Alternatively, we can solve this using fractions. Remember that 15% is equivalent to 15/100.
-
Step 1: Express the problem as a fraction multiplication: (15/100) * 65
-
Step 2: Simplify the fraction: This can be simplified before multiplication. Both 15 and 100 are divisible by 5, resulting in (3/20) * 65
-
Step 3: Perform the multiplication: (3/20) * 65 = 195/20
-
Step 4: Convert the improper fraction to a decimal: 195/20 = 9.75
Again, we arrive at the same answer: 15% of 65 is $\boxed{9.75}$.
Method 3: Proportion Method
The proportion method is a powerful technique for solving percentage problems, especially when dealing with more complex scenarios. It relies on setting up a proportion, which equates two ratios.
-
Step 1: Set up a proportion: We can set up a proportion as follows:
x / 65 = 15 / 100
Where 'x' represents the unknown value (15% of 65).
-
Step 2: Cross-multiply: Cross-multiplying gives us:
100x = 15 * 65
-
Step 3: Solve for x:
100x = 975 x = 975 / 100 x = 9.75
Once more, we find that 15% of 65 is $\boxed{9.75}$.
Method 4: Using a Calculator
Most calculators have a percentage function. Simply enter 65, press the multiplication button, enter 15, and then press the percentage button (%). The calculator will automatically perform the calculation and display the result: 9.75. This method is quick and efficient, especially for more complex percentage calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various aspects of life:
-
Finance: Calculating interest on loans, savings accounts, and investments. Determining discounts on purchases. Analyzing financial statements and reports. Understanding tax rates and calculating taxes owed.
-
Business: Calculating profit margins, markup percentages, and sales tax. Analyzing market share and growth rates. Determining employee bonuses and commissions. Evaluating the success of marketing campaigns.
-
Science: Expressing experimental results as percentages. Calculating statistical probabilities and confidence intervals. Analyzing data sets and trends.
-
Everyday Life: Calculating tips in restaurants. Understanding discounts and sales in stores. Figuring out the percentage of ingredients in a recipe. Interpreting statistics presented in news reports and articles.
Beyond the Basics: Working with More Complex Percentages
While this article focused on a simple percentage calculation, the principles can be applied to more complex problems. For example, consider these scenarios:
-
Finding the original amount: If 15% of a number is 9.75, what is the original number? This involves reversing the calculation using the formula: Original Number = (Percentage Amount / Percentage) * 100.
-
Calculating percentage increase or decrease: Determining the percentage change between two values requires calculating the difference between the values, dividing by the original value, and multiplying by 100.
-
Compound percentages: These calculations involve applying a percentage repeatedly, such as calculating compound interest over multiple periods.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a percentage of a number that isn't a whole number?
A: The methods described above work equally well with decimals. Simply convert the percentage to a decimal and multiply by the number.
-
Q: How can I improve my speed in calculating percentages?
A: Practice is key. The more you practice, the faster and more confident you'll become. Memorizing common percentage equivalents (e.g., 25% = 0.25, 50% = 0.50, etc.) can also help.
-
Q: Are there online calculators or tools that can help with percentage calculations?
A: Yes, many websites offer online percentage calculators. These can be helpful for quick calculations or for checking your work.
Conclusion: Mastering Percentages
Understanding percentages is a fundamental skill with far-reaching applications. While calculating 15% of 65 might seem trivial, mastering this concept empowers you to tackle more complex problems in various fields. By understanding the different methods of calculation and practicing regularly, you'll develop proficiency in this essential mathematical skill, transforming it from a simple calculation into a powerful tool for navigating numerous real-world challenges. Remember, the key is to grasp the underlying principles and choose the calculation method that best suits your needs and the complexity of the problem at hand. From simple discounts to complex financial analyses, the ability to work with percentages is an invaluable asset.
Latest Posts
Latest Posts
-
Subtracting Mixed Fractions Unlike Denominators
Sep 12, 2025
-
Divisible By 16 Numbers List
Sep 12, 2025
-
Ratios Equivalent To 4 6
Sep 12, 2025
-
12 13 As A Percentage
Sep 12, 2025
-
What Grade Is A 75
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 15 Percent Of 65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.