13 20 As A Percent
saludintensiva
Sep 09, 2025 · 5 min read
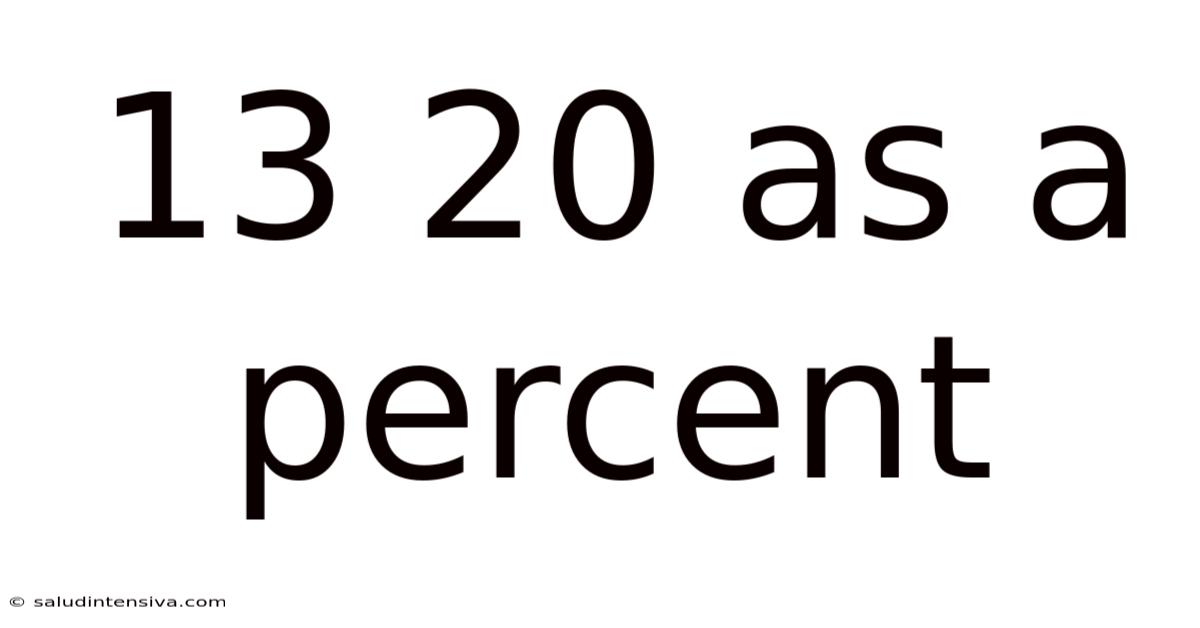
Table of Contents
Decoding 13/20 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating grades to understanding financial reports. This article will comprehensively explore how to convert the fraction 13/20 into a percentage, providing a step-by-step guide, exploring the underlying concepts, and addressing frequently asked questions. We will delve into the method, its significance, and offer practical examples to solidify your understanding. This guide aims to provide a clear and concise explanation, making this seemingly simple calculation understandable for everyone.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, 13/20 means 13 parts out of a total of 20 parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It indicates a proportion relative to a whole, where the whole is considered 100%. For example, 50% means 50 out of 100, or half.
Converting 13/20 to a Percentage: A Step-by-Step Guide
The conversion of a fraction to a percentage involves two primary steps:
Step 1: Convert the fraction to a decimal.
To achieve this, we simply divide the numerator (13) by the denominator (20):
13 ÷ 20 = 0.65
Step 2: Convert the decimal to a percentage.
This step involves multiplying the decimal by 100 and adding the percentage symbol (%):
0.65 × 100 = 65%
Therefore, 13/20 is equal to 65%.
Visual Representation of 13/20 as a Percentage
Imagine a pizza cut into 20 equal slices. If you eat 13 slices, you've consumed 65% of the pizza. This visual representation helps to grasp the concept of the fraction and its equivalent percentage. This simple analogy makes understanding percentages more intuitive, especially for those who struggle with abstract mathematical concepts.
The Significance of Understanding Percentage Conversions
The ability to convert fractions to percentages has several practical applications across various fields:
-
Academic Performance: Calculating grades often involves converting the number of correct answers to a percentage. For instance, if a student answers 13 out of 20 questions correctly on a test, their score is 65%.
-
Financial Literacy: Understanding percentages is crucial for comprehending interest rates, discounts, taxes, and other financial aspects. Being able to quickly convert fractions to percentages makes it easier to analyze financial information and make informed decisions.
-
Data Analysis: In data analysis and statistics, percentages are commonly used to represent proportions and trends within datasets. Converting fractions to percentages simplifies the interpretation of data and allows for easier comparisons.
-
Everyday Life: Percentages are ubiquitous in everyday life – from sales discounts ("20% off!") to weather reports ("65% chance of rain"). Mastering percentage calculations enhances your ability to interpret and utilize this information effectively.
Alternative Methods for Converting Fractions to Percentages
While the method described above is the most straightforward, there are other approaches to convert fractions to percentages:
-
Using Proportions: You can set up a proportion to solve for the percentage. For example:
13/20 = x/100
Solving for x using cross-multiplication (13 * 100 = 20 * x) yields x = 65, thus 65%.
-
Using a Calculator: Most calculators have a percentage function that directly converts fractions to percentages. Simply input the fraction (13/20) and press the percentage button.
Choosing the method depends on your preference and the tools available. The direct division method is generally the most efficient for simple fractions.
Expanding the Understanding: Working with Different Fractions
Let's explore a few more examples to reinforce the concept of converting fractions to percentages:
-
15/25: 15 ÷ 25 = 0.6 × 100 = 60%
-
7/10: 7 ÷ 10 = 0.7 × 100 = 70%
-
3/4: 3 ÷ 4 = 0.75 × 100 = 75%
These examples demonstrate the consistent application of the conversion process. Regardless of the specific fraction, the fundamental steps remain the same. Practice with a variety of fractions helps solidify your understanding and builds confidence in handling percentage calculations.
Addressing Common Misconceptions
One common mistake is confusing percentages with decimals. While they are closely related, they are not interchangeable. A decimal represents a part of a whole, just like a fraction, but a percentage explicitly represents that part as a proportion of 100. The conversion step of multiplying by 100 is essential to express the fraction as a percentage.
Another misconception arises when dealing with fractions that don't easily divide into whole numbers. For instance, converting 1/3 to a percentage results in a recurring decimal (0.333...). In such cases, you can either round the percentage to a certain number of decimal places (e.g., 33.33%) or express it as a fraction (33 1/3%). The level of precision required depends on the context.
Frequently Asked Questions (FAQ)
Q: Can I convert percentages back into fractions?
A: Absolutely! To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 65% becomes 65/100, which simplifies to 13/20.
Q: What if the denominator of the fraction is not easily divisible by 100?
A: You still follow the same steps: divide the numerator by the denominator to get a decimal, then multiply by 100 to obtain the percentage. You may get a decimal percentage, which can be rounded as needed.
Q: Are there any online tools or calculators to help with this conversion?
A: Yes, numerous online calculators and converters are available to perform this calculation quickly and easily. However, understanding the underlying process is crucial for building a strong mathematical foundation.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a valuable skill with wide-ranging applications. This article provided a comprehensive guide to converting 13/20 to 65%, outlining the step-by-step process, exploring the underlying concepts, and addressing common questions. Through practice and understanding the fundamental principles, you can confidently perform these conversions in various contexts, enhancing your mathematical proficiency and practical problem-solving abilities. Remember, mastering this skill is not just about getting the right answer; it's about developing a deeper understanding of how fractions and percentages relate to each other and how they are used to represent parts of a whole in different situations. Practice makes perfect – so keep practicing!
Latest Posts
Latest Posts
-
1 To The Third Power
Sep 10, 2025
-
4 20 In Decimal Form
Sep 10, 2025
-
320 Degrees Fahrenheit To Celsius
Sep 10, 2025
-
Equivalent Fractions For 4 12
Sep 10, 2025
-
5 16 As A Decimal
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 13 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.