5 16 As A Decimal
saludintensiva
Sep 10, 2025 · 6 min read
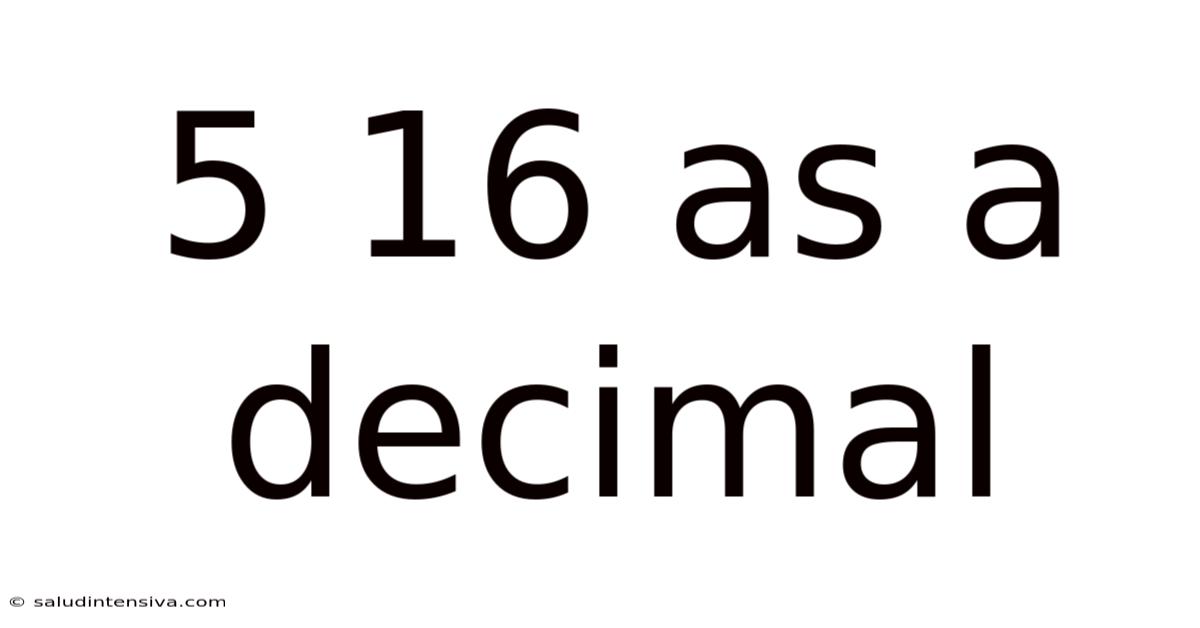
Table of Contents
Understanding 5/16 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications in science, engineering, and everyday life. This article provides a comprehensive explanation of how to convert the fraction 5/16 into its decimal equivalent, exploring multiple methods and delving into the underlying mathematical principles. We'll also address frequently asked questions and provide additional insights to solidify your understanding. By the end, you'll not only know the decimal value of 5/16 but also possess a deeper understanding of fraction-to-decimal conversions.
Introduction to Fraction-to-Decimal Conversion
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). A decimal, on the other hand, represents a number based on powers of ten. Converting a fraction to a decimal involves finding an equivalent representation of the fraction using a base-ten system. This is achieved primarily through division.
Method 1: Long Division
The most straightforward method to convert 5/16 to a decimal is through long division. This involves dividing the numerator (5) by the denominator (16):
-
Set up the division: Write 5 as the dividend (inside the division symbol) and 16 as the divisor (outside the division symbol).
-
Add a decimal point and zeros: Since 5 is smaller than 16, add a decimal point after the 5 and add as many zeros as needed to continue the division.
-
Perform the division: Divide 16 into 50. 16 goes into 50 three times (16 x 3 = 48). Subtract 48 from 50, leaving a remainder of 2.
-
Bring down the next zero: Bring down the next zero from the dividend to create 20.
-
Continue the process: 16 goes into 20 once (16 x 1 = 16). Subtract 16 from 20, leaving a remainder of 4.
-
Repeat: Bring down another zero to make 40. 16 goes into 40 twice (16 x 2 = 32). Subtract 32 from 40, leaving a remainder of 8.
-
Continue until you see a pattern or reach desired accuracy: Bring down another zero to make 80. 16 goes into 80 five times (16 x 5 = 80). The remainder is 0, indicating the division is complete.
Therefore, 5/16 = 0.3125.
Method 2: Using Equivalent Fractions
Another approach involves converting the fraction to an equivalent fraction with a denominator that is a power of 10. While this method isn't always directly applicable (as is the case with 5/16), understanding it provides a valuable alternative perspective.
Let's explore how this could work with fractions that have denominators easily convertible to powers of 10. For example, converting 1/4 to a decimal:
-
We know that 4 is a factor of 100 (4 x 25 = 100).
-
Multiply both the numerator and denominator by 25: (1 x 25) / (4 x 25) = 25/100.
-
25/100 is easily expressed as a decimal: 0.25.
Unfortunately, 16 doesn't have a simple conversion to a power of 10, making long division the more practical approach in this instance. However, this method highlights the underlying principle of finding an equivalent representation to simplify the decimal conversion.
Method 3: Using a Calculator
The simplest method, especially for complex fractions, is using a calculator. Simply enter 5 ÷ 16 and the calculator will display the decimal equivalent: 0.3125. While convenient, understanding the underlying mathematical processes (as explained in Method 1) is crucial for building a robust understanding of fractions and decimals.
The Significance of Decimal Representation
The decimal representation of 5/16, 0.3125, is a terminating decimal. This means the decimal representation ends, unlike repeating decimals which have a repeating sequence of digits. The fact that 5/16 results in a terminating decimal is directly related to the denominator. Denominators that are composed solely of factors of 2 and/or 5 (powers of 10) always produce terminating decimals. Since 16 = 2⁴, it only contains a factor of 2, resulting in a terminating decimal.
Understanding Terminating and Repeating Decimals
Let's clarify the difference between terminating and repeating decimals:
-
Terminating decimals: These decimals have a finite number of digits after the decimal point. Examples: 0.25, 0.75, 0.3125.
-
Repeating decimals: These decimals have an infinitely repeating sequence of digits after the decimal point. These are often represented with a bar over the repeating sequence. Examples: 1/3 = 0.3̅ (the 3 repeats infinitely), 1/7 = 0.142857̅ (the sequence 142857 repeats infinitely).
The type of decimal (terminating or repeating) depends entirely on the prime factorization of the denominator of the fraction. If the denominator's prime factorization contains only 2s and/or 5s, the decimal will terminate. If it contains any other prime factors, the decimal will repeat.
Applications of Decimal Conversions
The ability to convert fractions to decimals is vital in numerous fields:
-
Engineering and Physics: Precise calculations often require decimal representations for accuracy.
-
Finance: Calculating percentages, interest rates, and financial ratios.
-
Computer Science: Representing numerical data in computer systems.
-
Everyday Life: Measurements, cooking recipes, and general problem-solving.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be converted to decimals?
Yes, all fractions can be converted to decimals. The resulting decimal might be terminating or repeating.
Q2: What if the decimal conversion results in a repeating decimal? How do I represent it?
A repeating decimal is represented by placing a bar over the repeating sequence of digits. For example, 1/3 = 0.3̅.
Q3: Is there a shortcut method for converting fractions to decimals when the denominator is a power of 2?
While long division always works, you can sometimes use mental math shortcuts. Understanding powers of 2 (2, 4, 8, 16, 32, etc.) and their decimal equivalents can be helpful. For example, knowing that 1/2 = 0.5, 1/4 = 0.25, 1/8 = 0.125, and 1/16 = 0.0625 can help you quickly calculate related fractions.
Q4: Why is understanding this conversion important?
Converting fractions to decimals provides flexibility in calculations and is a cornerstone of mathematical literacy. It's essential for problem-solving in many fields, both academic and practical.
Conclusion
Converting 5/16 to its decimal equivalent, 0.3125, is easily achieved through long division, calculator use, or by understanding the concept of equivalent fractions (though less practical in this specific case). The process highlights the fundamental relationship between fractions and decimals and the importance of understanding the properties of terminating and repeating decimals. This knowledge is essential for mathematical proficiency and has wide-ranging applications in diverse fields. By mastering this skill, you enhance your problem-solving abilities and solidify your understanding of fundamental mathematical concepts.
Latest Posts
Latest Posts
-
9 20 As A Percent
Sep 10, 2025
-
1 9 100 As A Percent
Sep 10, 2025
-
Birth Year To Be 21
Sep 10, 2025
-
Is 4 5 Greater Than 3 4
Sep 10, 2025
-
90 Days After May 10th
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 5 16 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.