15 20 In Simplest Form
saludintensiva
Sep 22, 2025 · 6 min read
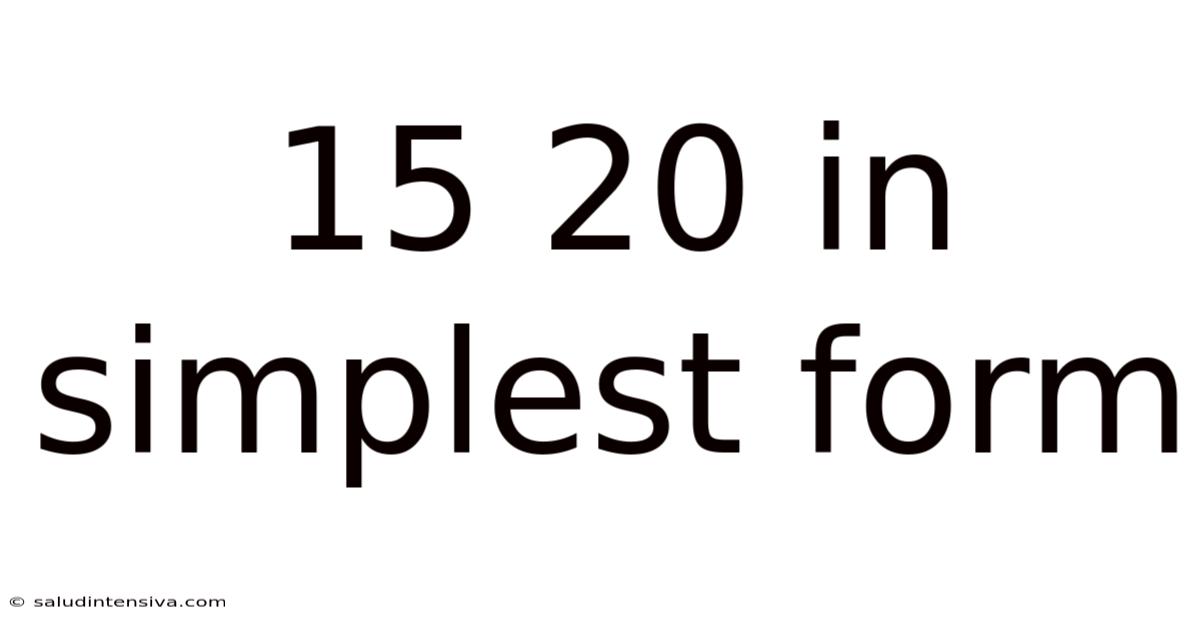
Table of Contents
Simplifying Fractions: A Deep Dive into 15/20
Understanding fractions is a fundamental skill in mathematics, essential for everything from baking a cake to understanding complex financial models. This article will delve into the simplification of the fraction 15/20, providing a step-by-step guide suitable for all levels, from beginners to those looking to refresh their knowledge. We'll explore the concept of greatest common divisors (GCD), equivalent fractions, and the importance of expressing fractions in their simplest form. By the end, you'll not only know the simplest form of 15/20 but also possess a strong understanding of the underlying principles involved.
Understanding Fractions
Before we tackle simplifying 15/20, let's quickly review what a fraction represents. A fraction is a way of expressing a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 15/20, 15 is the numerator and 20 is the denominator. This means we have 15 parts out of a possible 20 equal parts.
What Does "Simplest Form" Mean?
A fraction is in its simplest form, or lowest terms, when the numerator and denominator have no common factors other than 1. In other words, you cannot divide both the numerator and denominator by any whole number greater than 1 and still get whole numbers as a result. Simplifying a fraction doesn't change its value; it just represents it in a more concise and manageable way. Think of it like reducing a recipe – you can halve the ingredients, but the cake will still taste the same.
Finding the Simplest Form of 15/20: A Step-by-Step Guide
There are several ways to simplify a fraction, but the most efficient method involves finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest whole number that divides both numbers evenly.
Method 1: Finding the GCD using Prime Factorization
-
Find the prime factorization of the numerator (15): 15 can be broken down into its prime factors as 3 x 5. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
-
Find the prime factorization of the denominator (20): 20 can be written as 2 x 2 x 5, or 2² x 5.
-
Identify common factors: Both 15 and 20 share the prime factor 5.
-
Calculate the GCD: The GCD is the product of the common prime factors. In this case, the GCD of 15 and 20 is 5.
-
Simplify the fraction: Divide both the numerator and the denominator by the GCD (5):
15 ÷ 5 = 3 20 ÷ 5 = 4
Therefore, the simplest form of 15/20 is 3/4.
Method 2: Finding the GCD using the Euclidean Algorithm
The Euclidean algorithm is another efficient method for finding the GCD, especially for larger numbers. It involves repeatedly applying the division algorithm.
-
Divide the larger number (20) by the smaller number (15): 20 ÷ 15 = 1 with a remainder of 5.
-
Replace the larger number with the smaller number (15) and the smaller number with the remainder (5): Now we have 15 and 5.
-
Repeat the process: 15 ÷ 5 = 3 with a remainder of 0.
-
The GCD is the last non-zero remainder: The last non-zero remainder is 5, so the GCD of 15 and 20 is 5.
-
Simplify the fraction: As before, divide both the numerator and denominator by 5 to get 3/4.
Method 3: Identifying Common Factors by Inspection (Suitable for smaller numbers)
For smaller numbers like 15 and 20, you might be able to identify common factors by inspection. You can see that both 15 and 20 are divisible by 5. Dividing both by 5 gives you 3/4. This method is quicker for simple fractions but may become less efficient with larger numbers.
Equivalent Fractions
It's important to understand that simplifying a fraction doesn't change its value. Fractions that represent the same value are called equivalent fractions. For example, 15/20, 3/4, 75/100, and 150/200 are all equivalent fractions. They all represent three-quarters of a whole. Simplifying a fraction simply expresses the same value in a more concise way.
Why Simplify Fractions?
Simplifying fractions is crucial for several reasons:
-
Clarity and Understanding: A simplified fraction is easier to understand and interpret than a more complex one. 3/4 is clearly easier to grasp than 15/20.
-
Efficiency in Calculations: Working with simplified fractions makes calculations much easier and less prone to errors.
-
Standardization: Expressing fractions in their simplest form ensures consistency and facilitates comparisons.
-
Problem Solving: Many mathematical problems require simplifying fractions as an intermediate step in finding a solution.
Further Exploration: Working with Improper Fractions and Mixed Numbers
The principles of simplifying fractions apply equally to improper fractions (where the numerator is larger than the denominator) and mixed numbers (a combination of a whole number and a fraction).
For example, the improper fraction 27/12 can be simplified. First, find the GCD of 27 and 12, which is 3. Dividing both by 3 gives 9/4. This improper fraction can then be converted to a mixed number: 2 ¼.
Frequently Asked Questions (FAQ)
Q: What if I don't know how to find the prime factorization of a number?
A: There are many online resources and calculators that can help you find the prime factorization of any number. You can also use the Euclidean algorithm, which doesn't require prime factorization.
Q: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
A: No, you must divide both the numerator and the denominator by the same number to maintain the value of the fraction.
Q: Is there a shortcut for simplifying fractions?
A: For smaller numbers, you might be able to simplify by inspection. However, for larger numbers, using prime factorization or the Euclidean algorithm is more reliable.
Q: What if the GCD is 1?
A: If the GCD of the numerator and denominator is 1, it means the fraction is already in its simplest form.
Conclusion
Simplifying the fraction 15/20 to its simplest form, 3/4, is a straightforward process once you understand the underlying principles. Mastering fraction simplification is a fundamental building block for success in mathematics. By understanding the concepts of GCD, equivalent fractions, and the various methods for simplification, you'll be well-equipped to handle more complex fraction problems with confidence. Remember to practice regularly – the more you work with fractions, the more intuitive the process will become. This will not only improve your math skills but also enhance your ability to tackle various real-world problems involving ratios and proportions.
Latest Posts
Latest Posts
-
Multiplying Decimals Using Area Models
Sep 22, 2025
-
How Much Is 21 Kg
Sep 22, 2025
-
4400 Meters Squared To Feet
Sep 22, 2025
-
What Is 3 5 Of 5
Sep 22, 2025
-
What Time Is 19 39
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 15 20 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.