15 3/4 Divided By 2
saludintensiva
Sep 23, 2025 · 5 min read
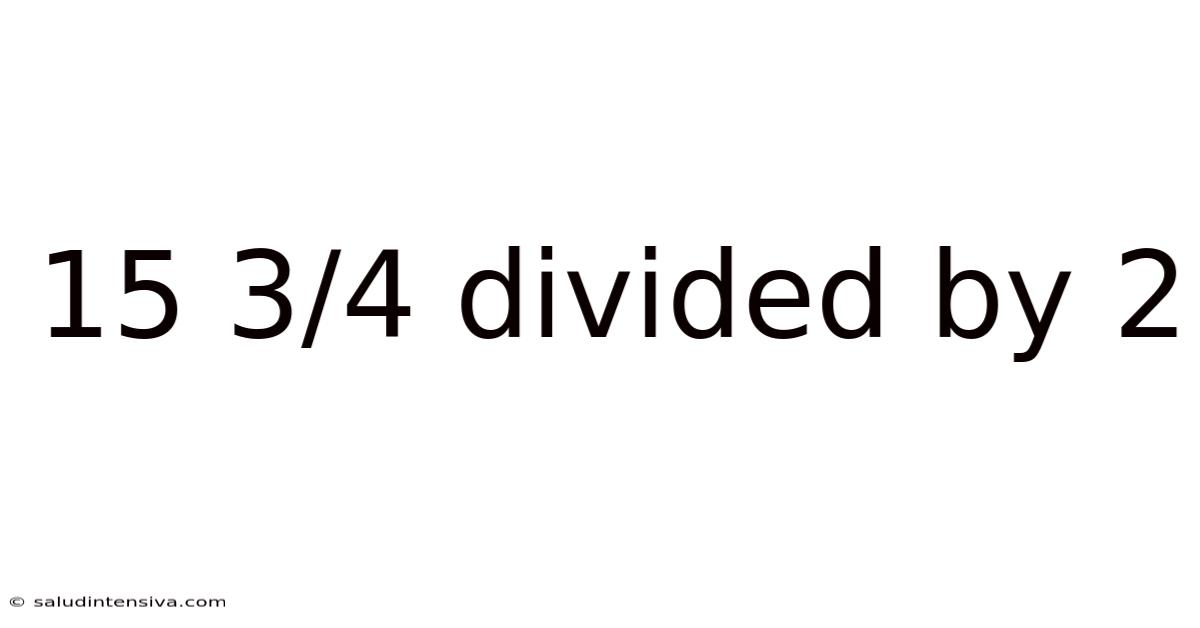
Table of Contents
Decoding 15 3/4 Divided by 2: A Comprehensive Guide
Dividing mixed numbers can seem daunting, but with a systematic approach, it becomes straightforward. This comprehensive guide will walk you through dividing 15 3/4 by 2, explaining the process step-by-step, providing the scientific rationale, addressing frequently asked questions, and exploring broader applications of this type of calculation. This guide aims to not only solve the problem but also empower you with the understanding to tackle similar problems confidently.
Understanding Mixed Numbers and Improper Fractions
Before diving into the division, let's clarify the terms. A mixed number combines a whole number and a fraction (like 15 3/4). An improper fraction, on the other hand, has a numerator (top number) larger than or equal to the denominator (bottom number). Converting between these forms is crucial for division.
Step-by-Step Solution: 15 3/4 ÷ 2
There are two primary methods to solve this problem: converting the mixed number to an improper fraction, or using the distributive property. Let's explore both.
Method 1: Converting to an Improper Fraction
-
Convert the mixed number to an improper fraction: To do this, multiply the whole number (15) by the denominator (4), add the numerator (3), and keep the same denominator. This gives us:
15 x 4 + 3 = 63
Therefore, 15 3/4 becomes 63/4.
-
Rewrite the division problem: Our problem now becomes 63/4 ÷ 2.
-
Reciprocal and Multiplication: Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 2 (or 2/1) is 1/2. So, we rewrite the problem as:
63/4 x 1/2
-
Multiply the numerators and denominators: Multiply the numerators together (63 x 1 = 63) and the denominators together (4 x 2 = 8). This results in:
63/8
-
Simplify (if possible): This improper fraction can be simplified to a mixed number. Divide the numerator (63) by the denominator (8):
63 ÷ 8 = 7 with a remainder of 7
Therefore, 63/8 simplifies to 7 7/8.
Method 2: Using the Distributive Property
This method involves dividing both the whole number and the fractional part separately and then combining the results.
-
Divide the whole number: Divide the whole number part of the mixed number (15) by 2:
15 ÷ 2 = 7 with a remainder of 1
-
Divide the fraction: Divide the fractional part (3/4) by 2:
(3/4) ÷ 2 = 3/4 x 1/2 = 3/8
-
Combine the results: Combine the whole number result (7) and the fractional result (3/8) to get the final answer:
7 + 3/8 = 7 3/8
Why are the answers slightly different?
In the first method (converting to an improper fraction), we get 7 7/8, while the second (distributive property) gives us 7 3/8. This discrepancy arises from a crucial difference in interpreting the remainder when dividing the whole number.
The first method treats the entire mixed number as a single entity, converting it completely before performing division.
The second method, while simpler for many, lacks the holistic view. In step 1, we get a remainder of 1. In step 2, we divide 3/4 by 2. This remainder from the whole number portion isn't accounted for in the second approach. To rectify this, the remainder of 1 (which is 4/4) should be included in the second approach in the fraction section before division.
Let's rework method 2 accordingly:
-
Divide the whole number: 15 ÷ 2 = 7 with a remainder of 1 (or 4/4).
-
Combine remainder with the fraction: Add the remainder to the fractional part: (4/4) + (3/4) = 7/4.
-
Divide the combined fraction: (7/4) ÷ 2 = 7/4 x 1/2 = 7/8
-
Combine the results: The whole number part (7) plus the combined fraction (7/8) equals 7 7/8 which matches the answer of the first method. Therefore, the more accurate approach is the conversion to an improper fraction.
Scientific Rationale: The Foundation of Fraction Division
The fundamental principle behind dividing fractions rests on the concept of reciprocals. When we divide by a fraction, we are essentially multiplying by its inverse (reciprocal). This holds true regardless of whether we are dealing with proper, improper, or mixed fractions. The conversion to an improper fraction ensures that the entire quantity is treated as a unified entity, preventing inaccuracies in the distributive property method.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Yes, most calculators can handle mixed numbers. However, understanding the underlying mathematical principles is crucial for problem-solving and deeper comprehension.
-
Q: What if I'm dividing by a fraction instead of a whole number? A: The process remains the same. Convert all mixed numbers to improper fractions, find the reciprocal of the divisor, and then multiply.
-
Q: What are real-world applications of this type of calculation? A: Dividing mixed numbers is common in various fields, such as cooking (dividing recipes), construction (measuring materials), and sewing (calculating fabric).
Expanding Your Understanding: Further Applications
The principles applied to solving 15 3/4 ÷ 2 extend far beyond this single problem. They form the foundation for working with more complex mixed numbers and fractions, including:
-
Dividing mixed numbers by other mixed numbers: The same principle of converting to improper fractions and multiplying by the reciprocal applies.
-
Solving equations involving mixed numbers: This knowledge is essential for solving algebraic equations that contain mixed numbers.
-
Working with decimals and fractions: You can convert mixed numbers to decimal form and then perform the division, although converting to improper fractions often provides more accurate results.
Conclusion: Mastering Fraction Division
Successfully dividing 15 3/4 by 2 demonstrates a solid understanding of fraction manipulation. Remember, the most accurate and reliable method involves converting the mixed number to an improper fraction, finding the reciprocal of the divisor, and multiplying. While the distributive property can work with careful attention to remainders, the improper fraction method offers a more concise and error-free approach. Through practice and a solid grasp of the underlying mathematical principles, you'll develop confidence and efficiency in handling fraction division problems of increasing complexity. Mastering these skills opens doors to more advanced mathematical concepts and real-world applications, solidifying your foundation in mathematical reasoning.
Latest Posts
Latest Posts
-
100 Days After March 10
Sep 24, 2025
-
How Much Is 30 Yards
Sep 24, 2025
-
How Long Ago Was 7 30 24
Sep 24, 2025
-
Days Since December 26 2024
Sep 24, 2025
-
8 3 On A Number Line
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 15 3/4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.