8/3 On A Number Line
saludintensiva
Sep 24, 2025 · 6 min read
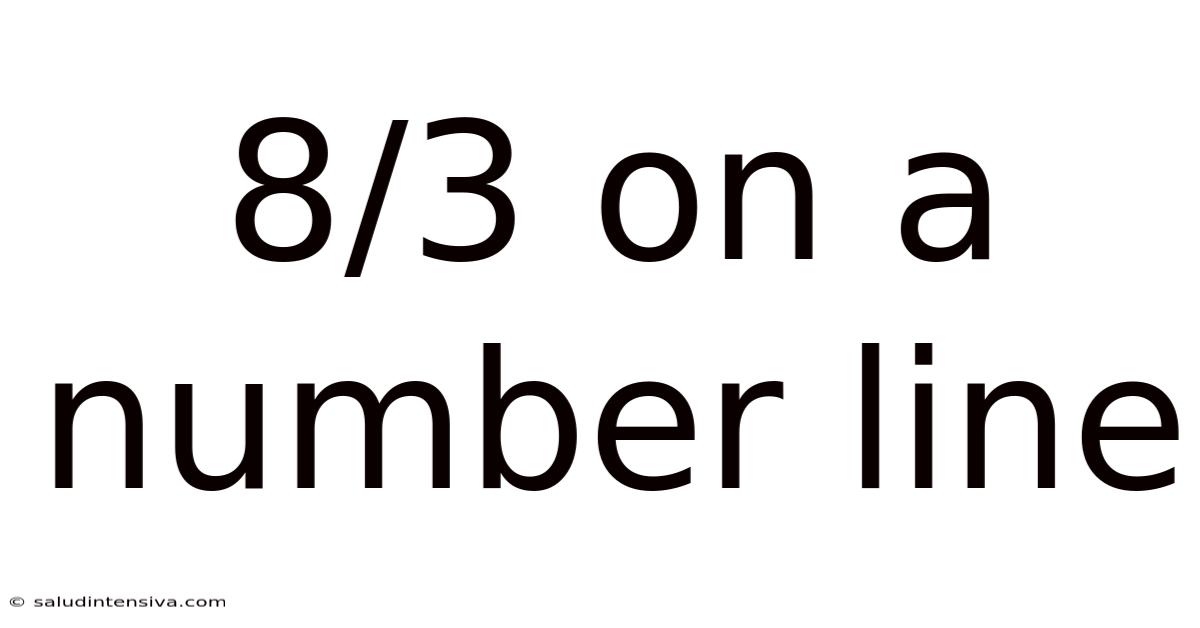
Table of Contents
Understanding 8/3 on the Number Line: A Comprehensive Guide
Locating fractions, especially improper fractions like 8/3, on a number line can seem daunting at first. However, with a clear understanding of the underlying concepts, this task becomes straightforward and even intuitive. This comprehensive guide will break down the process step-by-step, explaining not only how to place 8/3 on a number line but also the broader mathematical principles involved. We'll explore different approaches, address common misconceptions, and delve into the practical applications of this fundamental skill. By the end, you'll be confident in your ability to represent any fraction on a number line.
Understanding Fractions and Number Lines
Before we dive into placing 8/3 on the number line, let's refresh our understanding of key concepts. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts we're considering.
A number line is a visual representation of numbers, arranged in a sequential order. It's a powerful tool for understanding number relationships, comparing values, and visualizing operations like addition and subtraction. Zero is typically placed in the center, with positive numbers extending to the right and negative numbers extending to the left.
Improper fractions, like 8/3, are fractions where the numerator is greater than or equal to the denominator. This means the fraction represents a value greater than or equal to one. Understanding this is crucial for accurately placing it on a number line.
Method 1: Converting to a Mixed Number
One common approach to placing an improper fraction like 8/3 on a number line is to first convert it into a mixed number. A mixed number combines a whole number and a proper fraction (where the numerator is less than the denominator).
To convert 8/3 to a mixed number, we perform division:
8 ÷ 3 = 2 with a remainder of 2.
This means 8/3 is equivalent to 2 and 2/3. This representation makes it easier to visualize its position on the number line.
Plotting 8/3 (or 2 2/3) on the Number Line
-
Identify the Whole Number: The mixed number 2 2/3 tells us that the fraction lies between 2 and 3 on the number line.
-
Divide the Interval: We need to divide the interval between 2 and 3 into the number of parts indicated by the denominator of the fraction (which is 3). This creates three equal segments between 2 and 3.
-
Locate the Fraction: The numerator (2) tells us to move two segments to the right from the whole number 2. This places the point precisely at 2 2/3, or 8/3.
Method 2: Using Equal Parts
Alternatively, we can place 8/3 directly on the number line without converting to a mixed number. This method relies on understanding the meaning of the fraction itself.
-
Determine the scale: Consider a number line with whole numbers clearly marked. You need to visualize the fraction in relation to these whole numbers.
-
Divide into equal parts: The denominator (3) indicates that each whole number interval should be divided into 3 equal parts. This applies to every interval along the number line.
-
Locate the point: The numerator (8) tells us to count 8 of these equal parts starting from zero. Counting eight thirds from zero will lead directly to the position of 8/3 on the number line.
This approach is particularly helpful for visualizing the magnitude of the fraction and its relationship to other numbers.
Visual Representation and Practical Application
Imagine a number line stretching from 0 to 4. Each interval between whole numbers is divided into three equal parts, representing thirds. You would then count eight of these thirds from zero, landing precisely on the point representing 8/3.
This ability to visualize fractions on a number line has practical applications in various areas:
- Measurement: Imagine measuring a length that is 8/3 meters. A number line helps visualize this length accurately.
- Data Representation: Graphs and charts often use number lines to represent data. Understanding fractions is essential for interpreting such visual displays.
- Problem-solving: Many mathematical word problems can be solved more intuitively by visualizing them on a number line.
Addressing Common Misconceptions
A common mistake is to confuse the numerator and denominator, leading to incorrect placement on the number line. Remember, the denominator dictates the number of equal parts, while the numerator indicates how many of those parts are selected.
Another common error is not dividing the intervals equally. Ensure that each interval between whole numbers is partitioned into the precise number of parts indicated by the denominator. Unequal divisions will lead to inaccurate placement of the fraction.
Beyond 8/3: Extending the Concept
The methods described above are not limited to 8/3. They can be applied to any fraction, whether proper or improper. For example, to plot 11/4 on a number line:
- Convert to a mixed number (2 3/4).
- Divide the interval between 2 and 3 into four equal parts.
- Move three of these parts to the right from 2.
Alternatively, you can directly divide each whole number interval into four parts and count eleven of these parts from zero.
Frequently Asked Questions (FAQ)
Q: What if the fraction has a larger denominator?
A: The principle remains the same. Larger denominators simply mean more subdivisions of each whole number interval on the number line. The process becomes more precise but remains fundamentally the same.
Q: Can negative fractions be plotted on a number line?
A: Absolutely. Negative fractions are located on the left side of zero, mirroring the placement of their positive counterparts on the right side.
Q: How does this relate to decimal representation?
A: Fractions can be converted to decimals (8/3 ≈ 2.666...). Decimals offer another way to represent the fraction's position on a number line, providing an alternative method for plotting.
Conclusion: Mastering Fraction Representation
Placing a fraction like 8/3 on a number line is a fundamental skill in mathematics. This guide has provided a detailed explanation of two effective methods, highlighting the importance of understanding fractions, mixed numbers, and the principles of equal partitioning on the number line. By mastering this skill, you'll not only improve your understanding of fractions but also enhance your ability to visualize and solve mathematical problems in various contexts. Remember to practice regularly, and you will soon find this process intuitive and effortless. The key is to break down the process into manageable steps, focusing on the relationship between the numerator, denominator, and the divisions on the number line. With consistent practice, you’ll confidently navigate the world of fractions and their visual representation.
Latest Posts
Latest Posts
-
What Is 1 3 Of 21
Sep 24, 2025
-
73 Acres To Square Feet
Sep 24, 2025
-
What Is Discrete In Math
Sep 24, 2025
-
How To Remove Braces Brackets
Sep 24, 2025
-
Simple And Compound Interest Definition
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 8/3 On A Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.