15 Divided By 1 2
saludintensiva
Sep 21, 2025 · 6 min read
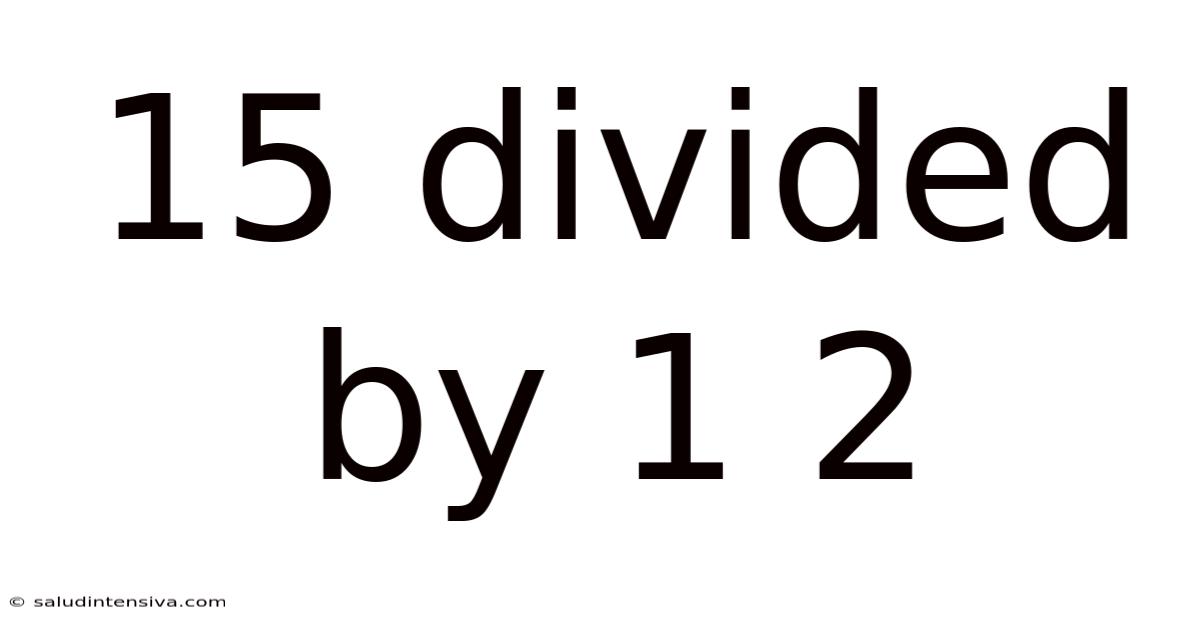
Table of Contents
15 Divided by 1/2: Unpacking the Seemingly Simple
Many people struggle with fractions, and even simple division problems involving fractions can seem daunting. This article will delve into the seemingly simple problem of 15 divided by 1/2, providing a comprehensive explanation suitable for all levels of mathematical understanding. We'll explore different approaches, explain the underlying principles, and address common misconceptions, ultimately aiming to build a solid understanding of fraction division. This will help you tackle more complex fraction problems with confidence.
Understanding the Problem: What Does it Mean?
Before we dive into the solution, let's clarify what the problem "15 divided by 1/2" actually means. It asks: "How many halves (1/2) are there in 15?" This rephrasing often makes the problem more intuitive. Instead of focusing on the abstract concept of division with fractions, we are now looking for the number of times 1/2 fits into 15.
Method 1: Visual Representation
Imagine you have 15 pizzas. Each pizza is cut into two equal halves (1/2). How many of these halves do you have in total? This is a simple multiplication problem: 15 pizzas * 2 halves/pizza = 30 halves. Therefore, there are 30 halves in 15 whole pizzas. This visual approach helps to grasp the concept before moving onto more abstract methods.
Method 2: The "Keep, Change, Flip" Method
This popular method provides a simple, mechanical way to solve division problems with fractions. It works as follows:
- Keep the first number (dividend) the same: 15
- Change the division sign (÷) to a multiplication sign (×)
- Flip (reciprocate) the second number (divisor): 1/2 becomes 2/1 (or simply 2)
So, the problem becomes: 15 × 2 = 30
This method works because dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3.
Method 3: Converting to Improper Fractions
This approach involves converting the whole number (15) into a fraction. We can write 15 as 15/1. The problem then becomes:
(15/1) ÷ (1/2)
Now, we use the rule for dividing fractions: Keep the first fraction, change the division sign to multiplication, and flip the second fraction:
(15/1) × (2/1) = 30/1 = 30
This method reinforces the principle of fraction division and shows the equivalence between different representations of numbers.
Method 4: Understanding the Reciprocal
The key to understanding why the "Keep, Change, Flip" method works lies in the concept of reciprocals. A reciprocal is a number that, when multiplied by the original number, equals 1. For example, the reciprocal of 2 is 1/2 (because 2 x 1/2 = 1), and the reciprocal of 1/2 is 2 (because 1/2 x 2 = 1).
When we divide by a fraction, we are essentially asking "how many times does this fraction fit into the whole number?" Dividing by 1/2 is the same as multiplying by its reciprocal, 2. This is because multiplying by 2 scales the quantity by a factor of two, effectively doubling it, and determining how many halves are present in the original quantity.
Explanation of the Principles Involved
The solution to 15 divided by 1/2 hinges on a crucial understanding of fraction division and the relationship between division and multiplication. Division is essentially the inverse operation of multiplication. When we divide 15 by 1/2, we are asking: "What number, when multiplied by 1/2, equals 15?"
The solution, 30, satisfies this condition because (1/2) x 30 = 15. This highlights the inverse relationship between multiplication and division.
Furthermore, the "Keep, Change, Flip" method is a shortcut that encapsulates the process of finding the multiplicative inverse (reciprocal) and applying the principle of converting division into multiplication. This method simplifies the calculation process, making it easier to handle more complex fraction division problems.
Addressing Common Misconceptions
A common mistake is to simply divide 15 by 2, yielding 7.5. This is incorrect because it does not account for the fact that we are dividing by a fraction, which represents a part of a whole, not a whole number. Dividing 15 by 2 would be appropriate if the problem were 15 divided by 2, not 15 divided by 1/2.
Another misconception is thinking that dividing by a fraction always results in a smaller number. In fact, dividing by a fraction less than 1 (like 1/2) results in a larger number because you are essentially finding how many times that fraction fits into the whole.
Extending the Concept: More Complex Problems
The principles learned from this example can be applied to more complex fraction division problems. For instance, consider the problem: 20 ÷ (3/4). Using the "Keep, Change, Flip" method:
20 ÷ (3/4) = 20 × (4/3) = 80/3 = 26 2/3
This demonstrates the versatility of the method in solving various types of fraction division problems.
Real-World Applications
Understanding fraction division is crucial in various real-world scenarios. For example:
- Cooking: A recipe calls for 1/2 cup of flour, but you want to triple the recipe. You would need to calculate 3 ÷ (1/2) = 6 cups of flour.
- Construction: Dividing lengths of materials into smaller fractional units (e.g., cutting a 15-foot board into pieces that are 1/2 foot long).
- Sewing: Calculating fabric requirements based on fractional measurements.
Frequently Asked Questions (FAQ)
-
Q: Why does flipping the fraction work? A: Flipping the fraction finds its reciprocal. Dividing by a number is the same as multiplying by its reciprocal.
-
Q: Can I use a calculator for this? A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is still essential.
-
Q: What if the dividend is also a fraction? A: The "Keep, Change, Flip" method still applies. For example, (2/3) ÷ (1/4) = (2/3) × (4/1) = 8/3.
-
Q: Is there another way to solve this besides "Keep, Change, Flip"? A: Yes, you can convert both numbers to decimals and then divide, or you can use the common denominator method for division of fractions. However, "Keep, Change, Flip" often is the easiest and most efficient.
Conclusion
Understanding how to divide by fractions is a fundamental skill in mathematics. While the problem of 15 divided by 1/2 might seem simple at first glance, it provides a solid foundation for grasping the core principles of fraction division. Through various methods, from visual representations to the "Keep, Change, Flip" technique, we have explored different approaches to solve this problem and others like it. By mastering these methods and understanding the underlying mathematical concepts, you'll be well-equipped to tackle more complex fraction problems with confidence and accuracy, whether in the classroom or in real-world applications. Remember, the key is to understand the why behind the calculations, not just the how. This understanding will make you a more proficient problem-solver and build a stronger foundation in mathematics.
Latest Posts
Latest Posts
-
1 13 As A Percent
Sep 21, 2025
-
Convert Gal To Cubic Feet
Sep 21, 2025
-
What 45 Celsius In Fahrenheit
Sep 21, 2025
-
What Is 15 Of 48
Sep 21, 2025
-
12 1000 As A Decimal
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 15 Divided By 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.