15 Out Of 20 Percent
saludintensiva
Sep 11, 2025 · 6 min read
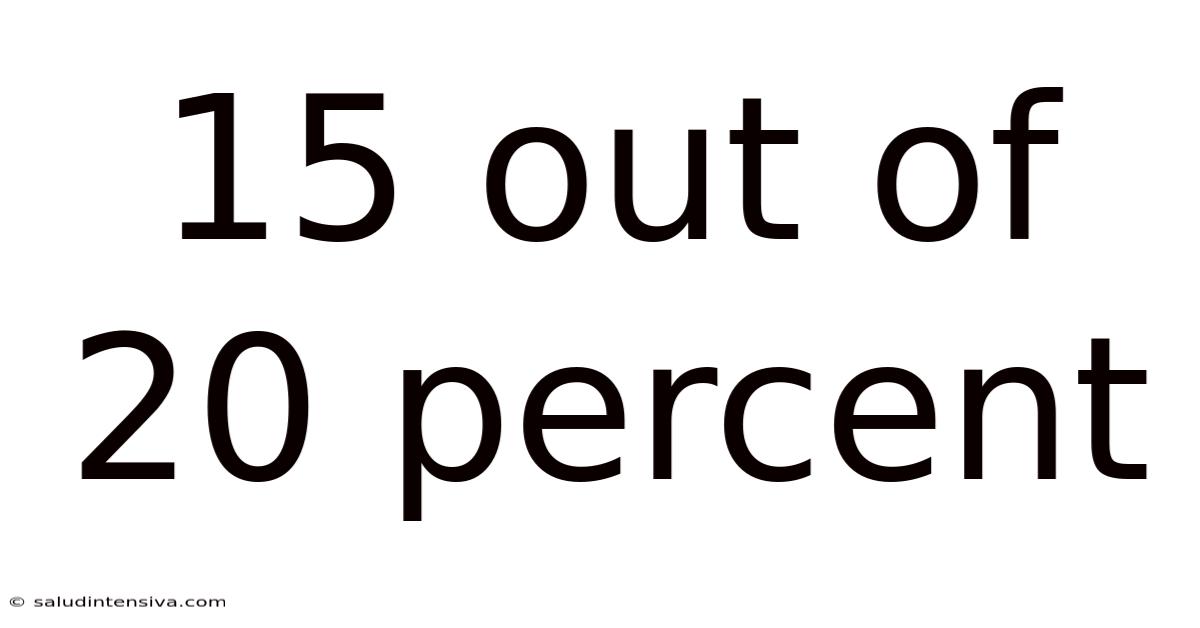
Table of Contents
Understanding 15 out of 20: Percentages, Fractions, and Real-World Applications
This article delves into the seemingly simple yet surprisingly multifaceted concept of "15 out of 20." We'll explore how to represent this as a fraction, a percentage, and a decimal, examining the underlying mathematical principles and showcasing its relevance in various real-world scenarios. Understanding this basic concept forms the foundation for more advanced mathematical applications, including statistics, probability, and data analysis. By the end, you'll not only know how to calculate 15 out of 20 but also grasp the broader implications of percentage calculations.
I. Expressing 15 out of 20: Different Representations
The phrase "15 out of 20" inherently signifies a part-to-whole relationship. It describes a portion (15) relative to a total (20). This can be expressed in several ways:
-
Fraction: The most straightforward representation is as a fraction: 15/20. This clearly indicates that 15 is the numerator (the part) and 20 is the denominator (the whole).
-
Simplified Fraction: Fractions can often be simplified by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 15 and 20 is 5. Therefore, 15/20 simplifies to 3/4. This equivalent fraction represents the same proportion.
-
Percentage: Percentages express a fraction as a proportion of 100. To convert 15/20 to a percentage, we divide the numerator by the denominator and multiply by 100: (15/20) * 100 = 75%. This means that 15 out of 20 represents 75% of the whole. Alternatively, since 3/4 is equivalent to 15/20, we can calculate (3/4) * 100 = 75%.
-
Decimal: Decimals are another way to express proportions. To convert 15/20 (or 3/4) to a decimal, we perform the division: 15 ÷ 20 = 0.75. This decimal value represents the same proportion as the fraction and percentage.
II. Mathematical Principles Involved
Understanding "15 out of 20" involves several key mathematical concepts:
-
Ratio: A ratio compares two quantities. In this case, the ratio is 15:20 (or 3:4 when simplified). Ratios are fundamental in many areas, from cooking recipes to map scales.
-
Proportion: A proportion shows the equality of two ratios. For instance, 15/20 = 75/100 is a proportion. Understanding proportions is crucial for solving problems involving scaling and similar shapes.
-
Percentage Calculation: The conversion of a fraction to a percentage is a common calculation used extensively in various fields, from finance to statistics. It provides a standardized way of comparing proportions.
-
Fraction Simplification: Reducing fractions to their simplest form makes them easier to understand and work with. This involves finding the GCD and dividing both the numerator and the denominator by it.
III. Real-World Applications
The concept of "15 out of 20" has numerous practical applications in everyday life:
-
Academic Performance: Imagine a student answering 15 questions correctly out of a total of 20 on a test. Their score would be 75%, reflecting their performance.
-
Sales and Marketing: A company might achieve 15 sales out of 20 potential clients. This translates to a 75% success rate, providing insights into sales effectiveness.
-
Manufacturing Quality Control: If a factory produces 20 items, and 15 meet quality standards, the quality control rate is 75%. This data helps identify areas for improvement in the production process.
-
Sports Statistics: In a basketball game, a player might make 15 out of 20 free throws. Their free throw percentage is 75%, a key indicator of their shooting accuracy.
-
Surveys and Polls: If 15 out of 20 respondents agree with a particular opinion in a survey, the agreement rate is 75%. This is vital for understanding public opinion.
-
Financial Investments: An investor might see a return of 15 units out of an initial investment of 20 units, resulting in a 75% return on investment.
-
Project Completion: If a project consists of 20 tasks, and 15 are completed, the project completion rate is 75%. This helps in tracking progress and managing deadlines.
IV. Extending the Concept: Variations and Problem Solving
The understanding of "15 out of 20" can be expanded to solve more complex problems. For example:
-
Finding the number of incorrect answers: If a student got 15 out of 20 questions correct, they got 20 - 15 = 5 questions incorrect.
-
Scaling the proportion: If a similar test had 50 questions, maintaining the same proportion, the student would be expected to answer (3/4) * 50 = 37.5 questions correctly. Since you can't have half a question, you would round this to either 37 or 38 depending on the context.
-
Calculating the percentage of incorrect answers: The percentage of incorrect answers would be (5/20) * 100 = 25%.
-
Inverse problems: If a student scored 60% on a test with 20 questions, how many did they get correct? This involves setting up a proportion: 60/100 = x/20. Solving for x gives x = 12 correct answers.
V. Practical Exercises
To solidify your understanding, try solving these problems:
-
A baker made 25 loaves of bread, and 15 were sold. What percentage of the loaves were sold?
-
A fruit seller had 30 oranges, and 21 were ripe. What fraction of the oranges were ripe? What percentage were ripe?
-
A student answered 18 questions correctly on a 24-question test. What was their percentage score?
-
A company achieved a 80% success rate in its sales campaign, selling 16 products. How many potential customers did they approach?
-
A farmer harvested 40 apples, and 25% were rotten. How many rotten apples were there?
VI. Frequently Asked Questions (FAQ)
-
Q: Why is simplifying fractions important? A: Simplifying fractions makes calculations easier and provides a clearer understanding of the proportion involved.
-
Q: Can percentages be greater than 100%? A: Yes, percentages can be greater than 100% when a quantity exceeds its initial value or a reference point.
-
Q: How do I convert a decimal to a percentage? A: Multiply the decimal by 100 and add a "%" symbol.
-
Q: What is the difference between a ratio and a proportion? A: A ratio compares two quantities, while a proportion shows the equality of two ratios.
-
Q: Why are percentages so widely used? A: Percentages provide a standard and easily understandable way to represent proportions, making comparisons straightforward.
VII. Conclusion
Understanding "15 out of 20" is more than just a simple calculation; it's a gateway to understanding fundamental mathematical concepts like fractions, percentages, decimals, ratios, and proportions. These concepts are essential tools in various fields, from academics and business to sports and everyday life. Mastering these foundational principles opens up possibilities for tackling more complex mathematical problems and interpreting data effectively in various real-world contexts. The ability to translate between fractions, percentages, and decimals allows for flexibility and deeper comprehension of proportional relationships, empowering you to analyze and interpret data with greater confidence.
Latest Posts
Latest Posts
-
Square Root Of 13 Simplified
Sep 12, 2025
-
What Is 4 5 Equal To
Sep 12, 2025
-
84 Degrees F To C
Sep 12, 2025
-
What Is A 1 5 Ratio
Sep 12, 2025
-
Equivalent Fraction Of 8 20
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 15 Out Of 20 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.