Square Root Of 13 Simplified
saludintensiva
Sep 12, 2025 · 4 min read
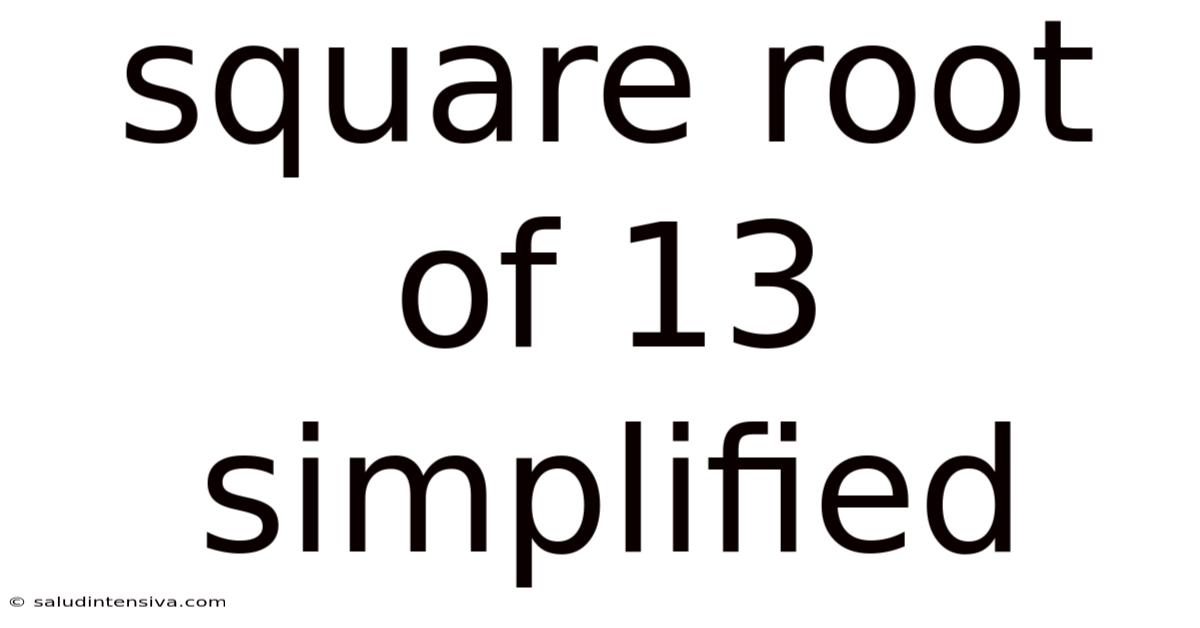
Table of Contents
Understanding and Simplifying the Square Root of 13
The square root of 13, denoted as √13, is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating. While we can't simplify it to a whole number or a neat fraction, we can explore different ways to understand and represent this number, improving our understanding of square roots and simplifying radicals. This article will delve into various methods of representing √13, exploring its properties and approximations. We will also address common misconceptions and frequently asked questions.
What is a Square Root?
Before diving into the specifics of √13, let's review the fundamental concept of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9. This is also written as 3². Similarly, the square root of 16 (√16) is 4 because 4 * 4 = 16, or 4².
The square root of 13, however, isn't a whole number. There's no integer that, when multiplied by itself, results in 13. This is why √13 is an irrational number.
Why Can't We Simplify √13 Further?
The simplification of square roots involves finding perfect square factors within the number under the radical sign (the radicand). A perfect square is a number that is the square of an integer (e.g., 4, 9, 16, 25, etc.). To simplify a square root, we look for perfect square factors and extract them.
For example, let's simplify √12. 12 can be factored as 4 * 3, and 4 is a perfect square (2²). Therefore, √12 can be simplified as √(4 * 3) = √4 * √3 = 2√3.
However, 13 is a prime number. This means its only factors are 1 and itself. It doesn't have any perfect square factors other than 1, which doesn't change the value of the square root. Therefore, √13 is already in its simplest form. We cannot simplify it any further.
Approximating √13
Since √13 is irrational, we cannot express it exactly as a decimal. However, we can find approximations. There are several methods to do this:
-
Using a Calculator: The simplest method is to use a calculator. Most calculators will provide an approximation of √13, typically to several decimal places (approximately 3.60555).
-
Using Estimation: We know that 3² = 9 and 4² = 16. Since 13 is between 9 and 16, √13 must be between 3 and 4. We can refine this estimation by considering that 13 is closer to 16 than to 9, suggesting that √13 is closer to 4 than to 3.
-
Using the Babylonian Method (or Heron's Method): This is an iterative method for approximating square roots. Start with an initial guess (let's say 3.5). Then, repeatedly apply the formula:
x_(n+1) = (x_n + N/x_n) / 2, wherex_nis the current approximation and N is the number whose square root we are seeking (in this case, 13). Each iteration will bring you closer to the actual value of √13.
Let's demonstrate one iteration:
- x₀ = 3.5 (initial guess)
- x₁ = (3.5 + 13/3.5) / 2 ≈ 3.607
Repeating this process several times will yield a progressively more accurate approximation.
Representing √13 Geometrically
We can also visualize √13 geometrically. Consider a right-angled triangle with legs of length 2 and 3. By the Pythagorean theorem (a² + b² = c²), the hypotenuse (c) has a length of √(2² + 3²) = √(4 + 9) = √13. Therefore, the length of the hypotenuse represents the value of √13.
√13 in Different Contexts
The square root of 13 appears in various mathematical and scientific contexts. For instance:
- Geometry: As shown above, it can represent the length of a diagonal or hypotenuse in a right-angled triangle.
- Algebra: It can be a solution to quadratic equations.
- Physics: It might appear in formulas related to distances, velocities, or other physical quantities.
Frequently Asked Questions (FAQs)
Q: Is √13 a rational or irrational number?
A: √13 is an irrational number. It cannot be expressed as a fraction of two integers.
Q: Can √13 be simplified?
A: No, √13 is already in its simplest form because 13 is a prime number and has no perfect square factors other than 1.
Q: What is the approximate value of √13?
A: The approximate value of √13 is 3.60555.
Q: How can I calculate √13 without a calculator?
A: You can use estimation methods or iterative methods like the Babylonian method to approximate the value.
Conclusion
While we cannot simplify √13 to a whole number or a simple fraction, understanding its properties as an irrational number and exploring methods for approximation enhances our comprehension of square roots and radical simplification. The inability to simplify √13 further doesn't diminish its importance; it simply highlights the nature of irrational numbers and their prevalence in mathematics and beyond. The geometrical representation, approximation methods, and understanding of its place within various mathematical and scientific fields further solidify our grasp of this seemingly simple yet fascinating mathematical concept. The exploration of √13 serves as a valuable stepping stone in understanding more complex mathematical concepts involving irrational numbers and radicals.
Latest Posts
Latest Posts
-
61 3 Percent Of 60 Questions
Sep 12, 2025
-
What Was 21 Weeks Ago
Sep 12, 2025
-
How To Simplify Big Fractions
Sep 12, 2025
-
Gcf Of 40 And 72
Sep 12, 2025
-
3 20 As A Mixed Number
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 13 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.