61.3 Percent Of 60 Questions
saludintensiva
Sep 12, 2025 · 5 min read
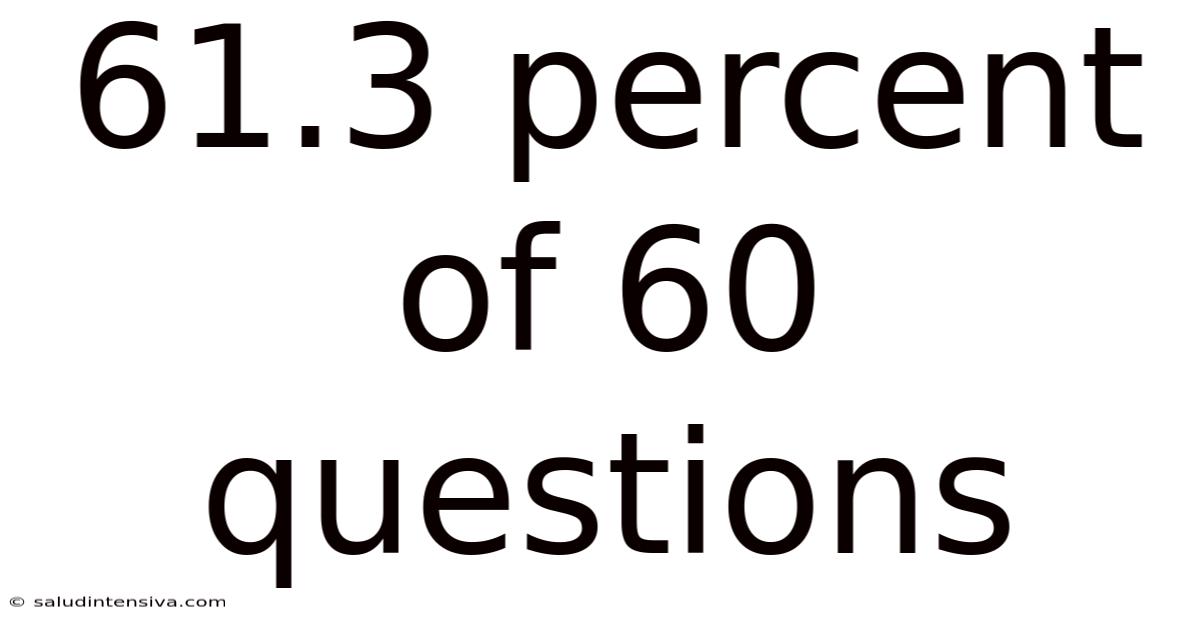
Table of Contents
Decoding 61.3 Percent of 60 Questions: A Deep Dive into Percentages and Proportions
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis. Understanding how to determine a percentage of a given number, such as finding 61.3 percent of 60 questions, is crucial for interpreting data and making informed decisions. This article provides a comprehensive explanation of how to perform this calculation, explores the underlying mathematical principles, and delves into the broader context of percentages and their applications. We'll also address common misconceptions and offer practical examples to solidify your understanding.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. For example, 50% represents 50 out of 100, which is equivalent to 1/2 or 0.5 in decimal form. Percentages are used extensively to represent proportions, ratios, and rates of change. They provide a standardized way to compare different quantities, regardless of their original units.
Calculating 61.3 Percent of 60 Questions: The Method
To determine 61.3 percent of 60, we need to convert the percentage to a decimal and then multiply it by the total number of questions. Here's a step-by-step breakdown:
-
Convert the percentage to a decimal: To convert a percentage to a decimal, divide the percentage by 100. In this case:
61.3% ÷ 100 = 0.613
-
Multiply the decimal by the total number of questions: Now, multiply the decimal representation of the percentage (0.613) by the total number of questions (60):
0.613 × 60 = 36.78
Therefore, 61.3 percent of 60 questions is 36.78 questions.
Interpreting the Result: Dealing with Fractions of Questions
The result, 36.78, presents a slight challenge in the context of questions. You cannot have a fraction of a question. This highlights the importance of understanding the context when dealing with percentages and proportions. In this scenario, we need to interpret the result based on the context.
-
Rounding: Depending on the context, you might round the result to the nearest whole number. Rounding 36.78 to the nearest whole number gives us 37 questions. This implies that approximately 37 out of 60 questions were answered correctly.
-
Precision: In some situations, maintaining the decimal precision is crucial. For example, if this represents a score in a high-stakes exam, simply rounding might not be appropriate. The 0.78 could represent a partial credit awarded for a partially correct answer.
-
Contextual Interpretation: The best way to interpret the result depends on the specifics of the situation. If it’s a test, how is partial credit handled? Is the result representing a percentage of correct answers, or is it a different metric? These questions inform how the calculation is used and interpreted.
Expanding the Concept: Proportions and Ratios
The calculation of 61.3% of 60 is fundamentally based on the concept of proportions and ratios. A ratio is a comparison of two quantities, and a proportion expresses the equality of two ratios. In this case, the proportion can be expressed as:
x/60 = 61.3/100
Where 'x' represents the number of questions representing 61.3%. Solving this proportion for 'x' leads to the same result as the method described earlier. This reinforces the connection between percentages, ratios, and proportions.
Real-World Applications: Beyond the Classroom
Understanding percentages and proportions is essential in various real-world situations:
-
Academic Performance: Calculating grades, analyzing test scores, and assessing overall academic progress all rely heavily on percentages.
-
Finance: Calculating interest rates, discounts, tax amounts, and analyzing financial statements involve extensive use of percentages.
-
Business and Marketing: Market share analysis, profit margins, sales growth calculations, and pricing strategies utilize percentages extensively.
-
Science and Engineering: Many scientific calculations and engineering designs involve the use of percentages to express concentrations, efficiencies, and error margins.
-
Everyday Life: Tip calculation, discount application during sales, and understanding nutritional information on food labels all involve working with percentages.
Common Misconceptions and Errors
Several common errors arise when working with percentages:
-
Incorrect Decimal Conversion: Failing to correctly convert the percentage to a decimal before performing the calculation is a frequent mistake.
-
Misunderstanding the Context: Ignoring the context and applying blanket rounding without considering the significance of the decimal part can lead to inaccurate interpretations.
-
Confusion with Percentage Increase/Decrease: A common mistake is confusing percentage change with the actual percentage of a quantity. For example, a 10% increase on a base value of 100 is 110, but 10% of 110 is different.
-
Incorrect Calculation of Percentage Change: To calculate a percentage increase or decrease, you need to find the difference between the new and old values and then divide by the old value.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a different percentage of 60?
A1: The same method applies. Simply replace 61.3% with the desired percentage, convert it to a decimal, and multiply by 60.
Q2: How can I check my answer?
A2: You can reverse the calculation. Divide the calculated value (36.78) by the total number (60) and multiply by 100 to verify if you obtain the original percentage (61.3%).
Q3: Can I use a calculator for these calculations?
A3: Absolutely! Calculators simplify the process, especially when dealing with more complex percentage calculations.
Q4: What are some online resources for practicing percentage calculations?
A4: Numerous websites and educational platforms offer practice exercises and tutorials on percentage calculations. These resources can help strengthen your understanding and skill.
Q5: How do I calculate percentage change?
A5: Percentage change is calculated as: [(New Value - Old Value) / Old Value] * 100. A positive result indicates an increase, while a negative result indicates a decrease.
Conclusion: Mastering Percentages for a Brighter Future
Understanding how to calculate percentages, such as finding 61.3 percent of 60, is a valuable skill with broad applications. By mastering this fundamental concept and understanding its underlying principles of proportions and ratios, you equip yourself with the tools to navigate various quantitative challenges in academic, professional, and personal contexts. The ability to accurately interpret and utilize percentages empowers you to analyze data effectively, make informed decisions, and confidently tackle numerical problems in diverse settings. Remember to always consider the context and interpret your results accordingly, ensuring accurate and meaningful conclusions. Continual practice and exploration of real-world applications will solidify your understanding and improve your proficiency in working with percentages.
Latest Posts
Latest Posts
-
9 1 2 As A Decimal
Sep 12, 2025
-
Cubic In To Cubic Yards
Sep 12, 2025
-
Convert 81 Kilos To Pounds
Sep 12, 2025
-
Mm Ft To Sq Ft
Sep 12, 2025
-
90 Days From 6 18
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 61.3 Percent Of 60 Questions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.