9 1/2 As A Decimal
saludintensiva
Sep 12, 2025 · 5 min read
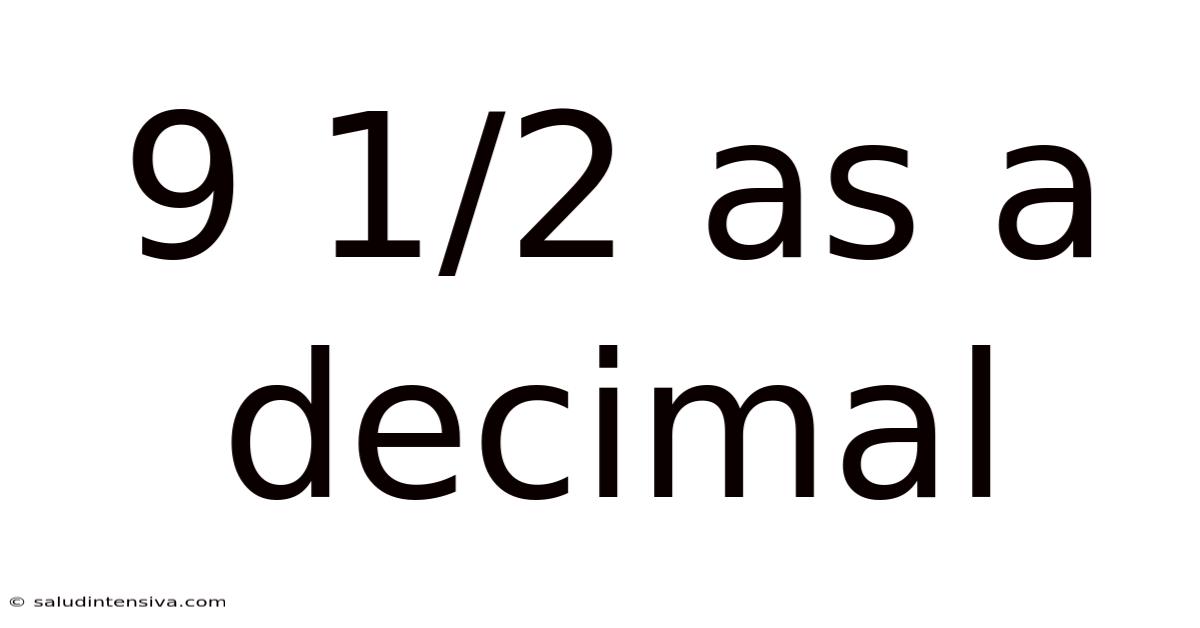
Table of Contents
9 1/2 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will delve into the conversion of the mixed number 9 1/2 into its decimal equivalent, exploring various methods and providing a deeper understanding of the underlying principles. We'll cover different approaches, address common misconceptions, and even explore the application of this conversion in real-world scenarios. This guide aims to provide a complete and thorough explanation, suitable for students of all levels, from elementary school to high school.
Understanding Mixed Numbers and Decimals
Before we dive into the conversion, let's refresh our understanding of mixed numbers and decimals. A mixed number combines a whole number and a fraction, like 9 1/2. This represents 9 whole units and half of another unit. A decimal, on the other hand, uses a base-ten system to represent numbers, with a decimal point separating the whole number part from the fractional part. For example, 9.5 is a decimal number. The digit after the decimal point represents tenths, the next digit represents hundredths, and so on.
Method 1: Converting the Fraction to a Decimal
The most straightforward method involves converting the fractional part of the mixed number (1/2) into a decimal and then adding it to the whole number part (9).
To convert 1/2 to a decimal, we perform the division: 1 ÷ 2 = 0.5
Therefore, 9 1/2 as a decimal is 9 + 0.5 = 9.5
Method 2: Converting the Mixed Number to an Improper Fraction
This method involves first converting the mixed number into an improper fraction and then converting the improper fraction to a decimal.
1. Convert to an Improper Fraction:
To convert 9 1/2 to an improper fraction, we multiply the whole number (9) by the denominator (2), add the numerator (1), and keep the same denominator (2).
(9 * 2) + 1 = 19
So, 9 1/2 becomes 19/2.
2. Convert the Improper Fraction to a Decimal:
Now, we divide the numerator (19) by the denominator (2):
19 ÷ 2 = 9.5
Therefore, 9 1/2 as a decimal is 9.5
Method 3: Using the Place Value System
This method highlights the relationship between fractions and decimals through the place value system. The fraction 1/2 represents one-half, or one out of two equal parts. In the decimal system, the first place after the decimal point represents tenths. Since 1/2 is equivalent to 5/10, it can be written as 0.5. Adding this to the whole number 9 gives us 9.5.
Understanding the Relationship Between Fractions and Decimals
The core concept underlying these conversions is the understanding that fractions and decimals are simply different ways of representing the same value. Fractions represent parts of a whole, while decimals utilize a base-ten system for expressing these parts. The ability to convert between fractions and decimals is crucial for various mathematical operations and real-world applications.
Common Misconceptions and How to Avoid Them
One common mistake is incorrectly converting the whole number directly. Remember that the whole number remains unchanged; only the fractional part needs conversion. Another misconception is forgetting the decimal point when converting from fraction to decimal. Pay close attention to the placement of the decimal point to ensure accuracy. Always double-check your work using different methods to ensure consistency and accuracy in your answer.
Real-World Applications of Decimal Conversions
The ability to convert fractions to decimals is not just a theoretical exercise. It has practical applications across various fields:
-
Finance: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals. For example, calculating a 50% discount (which is 1/2) on an item requires converting 1/2 to 0.5 to perform the calculation easily.
-
Measurement: Many measurements involve fractions (e.g., 9 1/2 inches), but calculations are often easier using decimals. Converting fractions to decimals allows for smoother calculations in engineering, construction, and other fields.
-
Data Analysis: In statistics and data analysis, converting fractional data into decimals is often necessary for calculations and representation in graphs and charts.
-
Science: Scientific measurements frequently use decimal notation for precision and ease of calculation. Converting fractional measurements to decimals ensures consistency in scientific data analysis.
Further Exploration: Converting More Complex Fractions
While 9 1/2 is a relatively simple conversion, the same principles apply to more complex fractions. For example, to convert a fraction like 7/8 to a decimal, simply divide 7 by 8: 7 ÷ 8 = 0.875. Similarly, to convert a mixed number like 3 5/16, you would first convert the fraction 5/16 to a decimal (5 ÷ 16 = 0.3125) and then add it to the whole number 3, giving 3.3125.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 9 1/2 to a decimal?
A: Yes, absolutely. Most calculators have the functionality to perform this conversion directly or by performing the division 19/2.
Q: What if the fraction has a repeating decimal?
A: Some fractions, when converted to decimals, result in repeating decimals (e.g., 1/3 = 0.333...). In such cases, you can either use the repeating decimal notation (e.g., 0.3̅) or round the decimal to a certain number of decimal places depending on the required level of accuracy.
Q: Why is understanding this conversion important?
A: Understanding fraction-to-decimal conversions is vital for various mathematical operations and real-world applications, making calculations more efficient and accurate. It’s a cornerstone of mathematical fluency.
Q: Are there other ways to represent 9 1/2?
A: Yes! Besides 9.5, you could also represent it as a percentage (950%), or as a ratio (19:2). Each representation offers a different perspective on the same value.
Conclusion
Converting 9 1/2 to its decimal equivalent, 9.5, is a straightforward process achievable using multiple methods. Understanding these methods not only reinforces your knowledge of fractions and decimals but also provides a strong foundation for more complex mathematical concepts and real-world applications. Remember to practice these methods with different fractions and mixed numbers to solidify your understanding and build confidence in your mathematical abilities. The more you practice, the more comfortable and proficient you will become in handling these conversions. This skill is a fundamental building block in your mathematical journey, paving the way for more advanced concepts and problem-solving abilities.
Latest Posts
Latest Posts
-
13 16 As A Decimal
Sep 12, 2025
-
14 Acres To Sq Ft
Sep 12, 2025
-
List Of Multiples Of 8
Sep 12, 2025
-
Lcm Of 25 And 35
Sep 12, 2025
-
46 Degrees C To F
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 9 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.