16 20 In Simplest Form
saludintensiva
Sep 18, 2025 · 6 min read
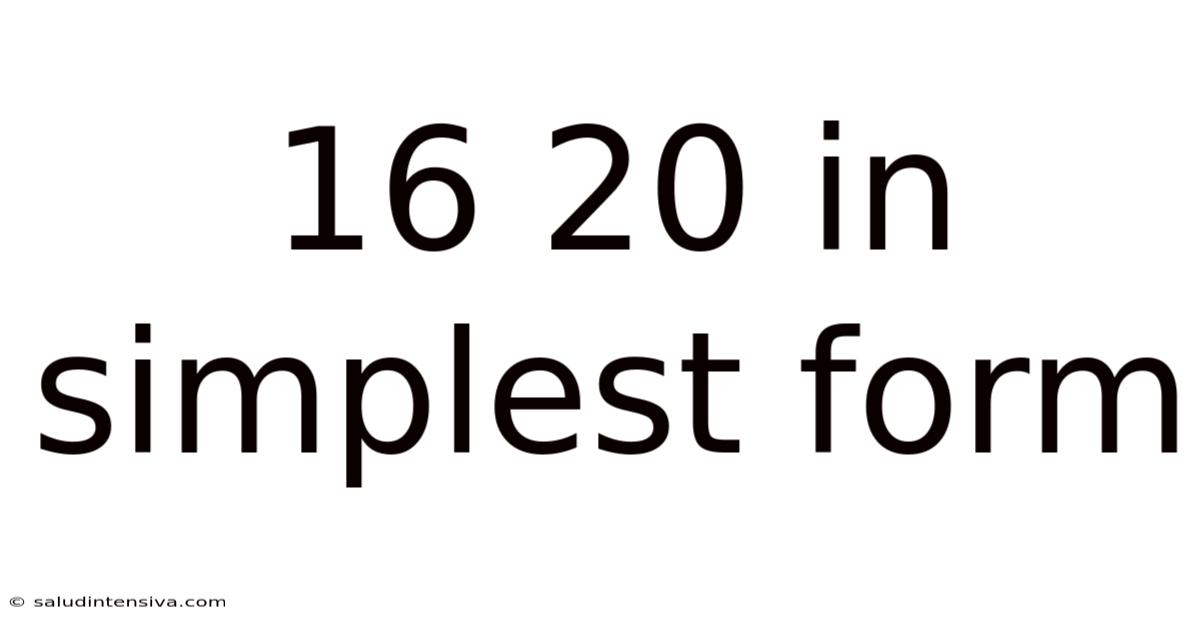
Table of Contents
Simplifying Fractions: Understanding 16/20 in its Simplest Form
Finding the simplest form of a fraction is a fundamental concept in mathematics. It's about expressing a fraction in its most concise and efficient representation, without altering its value. This article will delve into the process of simplifying fractions, using the example of 16/20, and will explore the underlying mathematical principles involved. We'll cover various methods, explain the importance of simplifying, and answer frequently asked questions. By the end, you'll not only understand how to simplify 16/20 but also possess the tools to simplify any fraction.
Understanding Fractions
Before we dive into simplifying 16/20, let's briefly review the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 16/20, 16 is the numerator and 20 is the denominator.
The Concept of Simplifying Fractions
Simplifying a fraction means reducing it to its lowest terms. This is achieved by dividing both the numerator and the denominator by their greatest common divisor (GCD), also known as the greatest common factor (GCF). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Simplifying a fraction doesn't change its value; it merely represents it in a more efficient form.
Method 1: Finding the Greatest Common Divisor (GCD)
The most common and reliable method for simplifying fractions is by finding the GCD of the numerator and the denominator. Let's apply this to 16/20.
-
Find the factors of the numerator (16): The factors of 16 are 1, 2, 4, 8, and 16.
-
Find the factors of the denominator (20): The factors of 20 are 1, 2, 4, 5, 10, and 20.
-
Identify the common factors: The common factors of 16 and 20 are 1, 2, and 4.
-
Determine the greatest common factor (GCF): The largest common factor is 4. Therefore, the GCD of 16 and 20 is 4.
-
Simplify the fraction: Divide both the numerator and the denominator by the GCD (4):
16 ÷ 4 = 4 20 ÷ 4 = 5
Therefore, the simplest form of 16/20 is 4/5.
Method 2: Prime Factorization
Another effective method for finding the GCD is through prime factorization. Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves).
-
Find the prime factorization of 16: 16 = 2 x 2 x 2 x 2 = 2⁴
-
Find the prime factorization of 20: 20 = 2 x 2 x 5 = 2² x 5
-
Identify common prime factors: Both 16 and 20 share two factors of 2 (2²).
-
Find the GCD: The GCD is the product of the common prime factors raised to the lowest power. In this case, it's 2² = 4.
-
Simplify the fraction: Divide both the numerator and the denominator by the GCD (4), resulting in 4/5.
Method 3: Repeated Division
This method involves repeatedly dividing both the numerator and the denominator by common factors until no common factors remain.
-
Start with a common factor: Notice that both 16 and 20 are divisible by 2.
-
Divide both by 2: 16 ÷ 2 = 8 20 ÷ 2 = 10
-
Check for further common factors: Both 8 and 10 are divisible by 2.
-
Divide both by 2 again: 8 ÷ 2 = 4 10 ÷ 2 = 5
Now, 4 and 5 have no common factors other than 1. Therefore, the simplified fraction is 4/5.
Why is Simplifying Fractions Important?
Simplifying fractions is crucial for several reasons:
-
Clarity and Conciseness: Simplified fractions are easier to understand and work with. 4/5 is much clearer than 16/20.
-
Accuracy in Calculations: Using simplified fractions reduces the risk of errors in further calculations. Working with smaller numbers is generally simpler and less prone to mistakes.
-
Standardized Representation: Simplifying ensures a consistent and universally accepted representation of a fraction.
-
Easier Comparisons: Comparing simplified fractions is much easier than comparing unsimplified ones. For example, comparing 4/5 to 3/4 is significantly easier than comparing 16/20 to 15/20.
Visual Representation of 16/20 and 4/5
Imagine a pizza cut into 20 equal slices. 16/20 represents having 16 of those slices. Now imagine a smaller pizza cut into 5 equal slices. 4/5 represents having 4 of those slices. While the amounts of pizza are different in size, the proportion of pizza you have is the same in both cases – four-fifths. This visually demonstrates that simplifying a fraction doesn't change its value.
Applications of Simplifying Fractions in Real Life
Simplifying fractions isn't just an abstract mathematical concept; it has practical applications in various real-world scenarios:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Simplifying fractions makes it easier to measure and understand the quantities needed.
-
Construction and Engineering: Precise measurements and calculations are essential in construction and engineering. Simplifying fractions ensures accuracy in these calculations.
-
Financial Calculations: In finance, dealing with fractions of currency and percentages is common. Simplifying fractions enhances efficiency and accuracy in financial calculations.
Frequently Asked Questions (FAQs)
Q1: What if I simplify a fraction incorrectly?
A1: If you don't divide by the greatest common divisor, you'll still get a simpler fraction, but it won't be in its lowest terms. You'll need to repeat the simplification process until you reach the lowest terms.
Q2: Can I simplify fractions with negative numbers?
A2: Yes, the process remains the same. Find the GCD of the absolute values of the numerator and denominator, and then apply the negative sign to the resulting fraction if the original fraction was negative. For example, -16/20 simplifies to -4/5.
Q3: What if the numerator is larger than the denominator?
A3: That's an improper fraction. You can simplify it using the same methods. After simplification, you might choose to convert it to a mixed number (a whole number and a fraction). For example, 20/16 simplifies to 5/4, which can be expressed as 1 ¼.
Q4: Is there a shortcut for simplifying fractions?
A4: While there isn't a single universal shortcut, recognizing small common factors quickly can speed up the process. For instance, if you notice both numbers are even, you can immediately divide by 2.
Conclusion
Simplifying fractions is a fundamental skill in mathematics with practical applications across various fields. By understanding the concept of the greatest common divisor and applying the methods discussed – finding the GCD, prime factorization, or repeated division – you can efficiently simplify any fraction, ensuring clarity, accuracy, and a standardized representation of fractional values. Remember, the key is to divide both the numerator and denominator by their greatest common divisor until no further common factors exist. This article has provided you with a thorough understanding of the process and the reasons behind its importance, equipping you with the skills to confidently simplify fractions in any context. Now, go forth and simplify!
Latest Posts
Latest Posts
-
When Was 29 Weeks Ago
Sep 18, 2025
-
85 Degrees Farenheit To Celcius
Sep 18, 2025
-
How To Figure Out Yards
Sep 18, 2025
-
Lcm Of 18 And 42
Sep 18, 2025
-
24 Degrees F To C
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 16 20 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.