Lcm Of 18 And 42
saludintensiva
Sep 18, 2025 · 5 min read
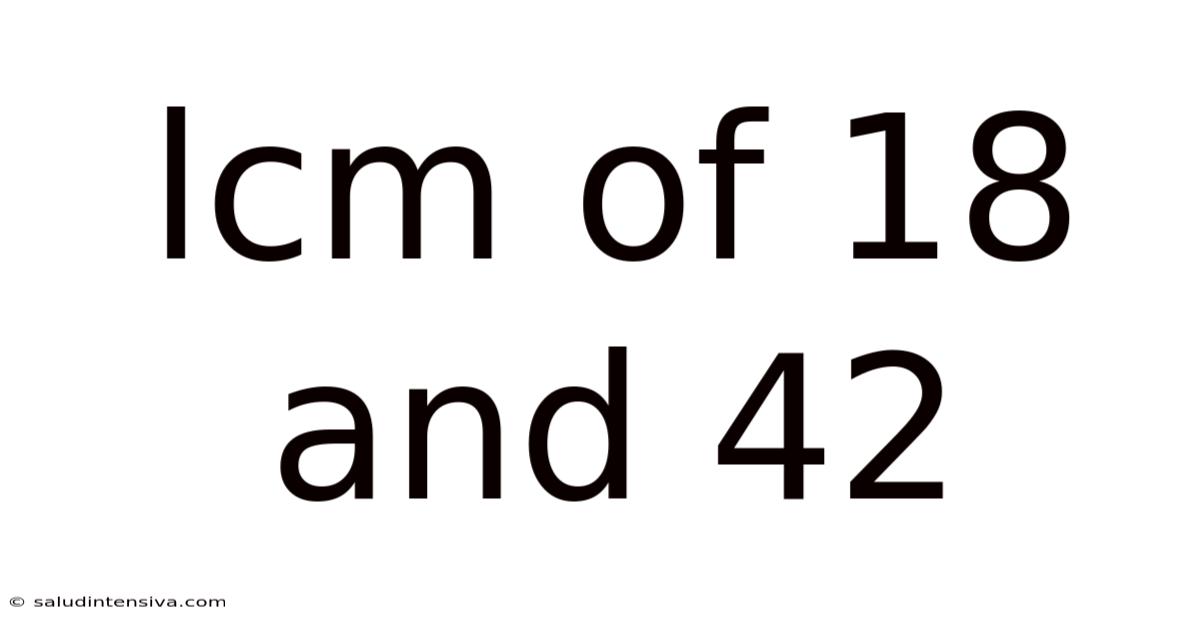
Table of Contents
Finding the Least Common Multiple (LCM) of 18 and 42: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation provides a strong foundation for more advanced mathematical concepts. This article delves into the process of finding the LCM of 18 and 42, exploring various methods, explaining the underlying principles, and providing a deeper understanding of the concept. We'll cover everything from the fundamental definitions to advanced techniques, ensuring a comprehensive grasp of the subject. This will be especially helpful for students learning about multiples, factors, and prime factorization.
Introduction: Understanding Multiples and Least Common Multiples
Before jumping into the calculation, let's clarify some fundamental terms. A multiple of a number is the product of that number and any integer. For example, multiples of 18 are 18, 36, 54, 72, 90, and so on. Similarly, multiples of 42 are 42, 84, 126, 168, 210, and so forth.
The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Finding the LCM is crucial in various mathematical applications, including solving problems involving fractions, ratios, and rhythmic patterns.
Method 1: Listing Multiples
The simplest, albeit less efficient for larger numbers, method is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, ...
- Multiples of 42: 42, 84, 126, ...
By comparing the lists, we observe that the smallest number appearing in both lists is 126. Therefore, the LCM of 18 and 42 using this method is 126. This method works well for smaller numbers, but becomes cumbersome and time-consuming for larger numbers.
Method 2: Prime Factorization
This method is more efficient and systematic, especially when dealing with larger numbers. It relies on the concept of prime factorization, which involves expressing a number as a product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
-
Find the prime factorization of each number:
- 18: 2 x 3 x 3 = 2 x 3²
- 42: 2 x 3 x 7
-
Identify the highest power of each prime factor present in either factorization:
- The prime factors are 2, 3, and 7.
- The highest power of 2 is 2¹ (from 18 or 42).
- The highest power of 3 is 3² (from 18).
- The highest power of 7 is 7¹ (from 42).
-
Multiply the highest powers of all prime factors together:
LCM(18, 42) = 2¹ x 3² x 7¹ = 2 x 9 x 7 = 126
Therefore, the LCM of 18 and 42 using prime factorization is 126. This method is significantly more efficient for larger numbers because it avoids the lengthy process of listing multiples.
Method 3: Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the Greatest Common Divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. There's a useful formula connecting the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
-
Find the GCD of 18 and 42: We can use the Euclidean algorithm for this.
- 42 = 2 x 18 + 6
- 18 = 3 x 6 + 0
The last non-zero remainder is the GCD, which is 6.
-
Apply the formula:
LCM(18, 42) = (18 x 42) / GCD(18, 42) = (18 x 42) / 6 = 126
Therefore, the LCM of 18 and 42 using the GCD method is 126. This method is efficient and particularly useful when dealing with larger numbers where prime factorization might be more time-consuming.
Why is the LCM Important? Real-World Applications
Understanding LCM extends beyond theoretical mathematics. It has practical applications in various fields:
-
Scheduling: Imagine two buses departing from the same station at different intervals. Finding the LCM of their departure intervals helps determine when they will depart simultaneously again.
-
Fraction Arithmetic: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator, simplifying the calculation.
-
Patterning and Cycles: In areas like music or construction, repetitive patterns can be analyzed using LCM to find the point of convergence or repetition.
-
Gear Ratios: In mechanical engineering, gear ratios often involve finding the LCM to determine the synchronized rotation of multiple gears.
Frequently Asked Questions (FAQ)
-
What if one of the numbers is zero? The LCM of any number and zero is undefined because zero has infinitely many multiples.
-
What if the numbers are the same? If the two numbers are identical, the LCM is simply the number itself. For example, LCM(18, 18) = 18.
-
Can I use a calculator to find the LCM? Yes, many calculators have built-in functions to calculate the LCM of two or more numbers.
-
Which method is the best? The prime factorization method is generally the most efficient and reliable for larger numbers, while the listing method is suitable for smaller numbers where visualization is helpful. The GCD method is also efficient but requires an additional step of finding the GCD.
Conclusion: Mastering the LCM
Finding the least common multiple is a fundamental skill in mathematics with practical applications across numerous disciplines. We've explored three different methods: listing multiples, prime factorization, and the GCD method, each offering unique advantages depending on the numbers involved. Understanding these methods not only helps in calculating the LCM but also strengthens the foundational understanding of multiples, factors, prime numbers, and the relationship between the LCM and GCD. By mastering these concepts, you'll be well-equipped to tackle more complex mathematical problems and appreciate the elegance and practicality of this seemingly simple arithmetic operation. Remember that the key is understanding the underlying principles, and choosing the most efficient method based on the context. The LCM of 18 and 42, regardless of the method used, remains consistently 126.
Latest Posts
Latest Posts
-
Is 37 Prime Or Composite
Sep 18, 2025
-
5 10 In Simplest Form
Sep 18, 2025
-
List The Multiples Of 3
Sep 18, 2025
-
4 25 As A Percent
Sep 18, 2025
-
Odds Of Winning Raffle Calculator
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 18 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.