5 10 In Simplest Form
saludintensiva
Sep 18, 2025 · 6 min read
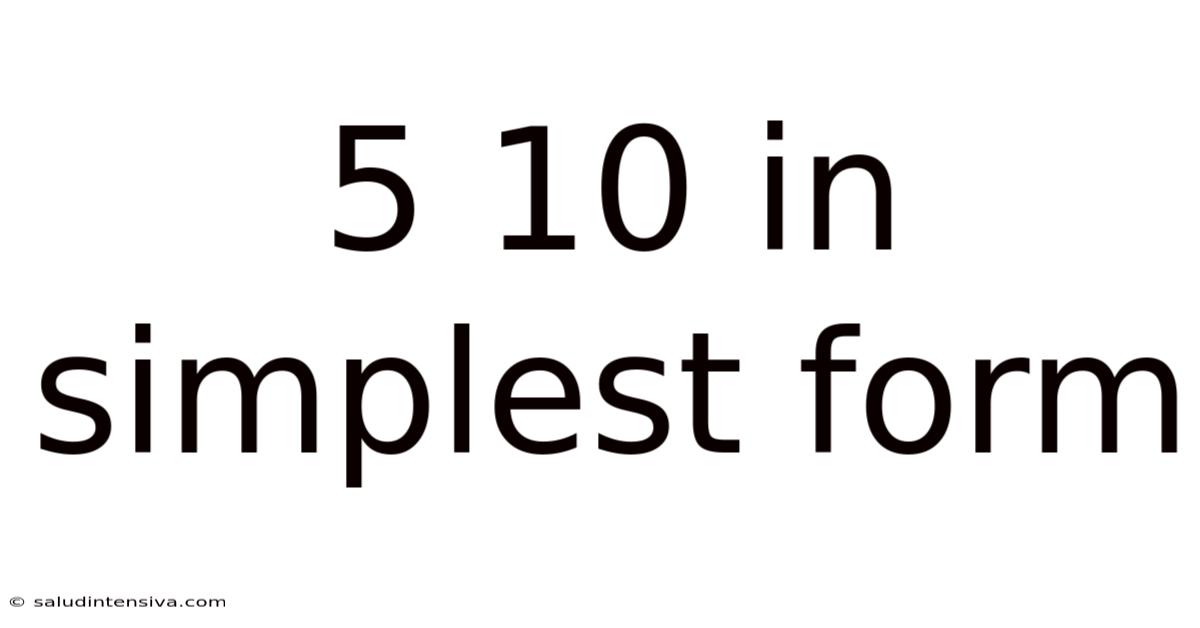
Table of Contents
Simplifying Fractions: Mastering the Art of 5/10
Understanding fractions is a cornerstone of mathematics, vital for everything from baking a cake to understanding complex financial models. This article delves into the simplification of fractions, focusing specifically on how to reduce 5/10 to its simplest form. We'll explore the underlying principles, provide step-by-step instructions, and address common misconceptions, equipping you with the confidence to tackle similar fraction simplification problems. This guide is perfect for students, educators, and anyone looking to refresh their understanding of fundamental mathematical concepts.
Understanding Fractions: A Quick Refresher
Before we dive into simplifying 5/10, let's briefly review what a fraction represents. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. For example, in the fraction 5/10, 5 is the numerator and 10 is the denominator. This means we have 5 parts out of a total of 10 equal parts.
Why Simplify Fractions?
Simplifying, or reducing, a fraction means expressing it in its lowest terms. This doesn't change the fraction's value; it simply makes it easier to understand and work with. Simplified fractions are more concise and easier to compare with other fractions. Imagine trying to compare 24/48 with 12/24 versus comparing 1/2 with 1/2 – the latter is clearly much simpler. Simplifying fractions is crucial for accurate calculations and clearer mathematical representation.
Finding the Simplest Form of 5/10: A Step-by-Step Guide
Simplifying 5/10 involves finding the greatest common divisor (GCD) of the numerator (5) and the denominator (10). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Step 1: Identify the Factors
Let's list the factors of both 5 and 10:
- Factors of 5: 1, 5
- Factors of 10: 1, 2, 5, 10
Step 2: Find the Greatest Common Divisor (GCD)
By comparing the lists, we see that the largest number that divides both 5 and 10 is 5. Therefore, the GCD of 5 and 10 is 5.
Step 3: Divide Both the Numerator and Denominator by the GCD
Now, we divide both the numerator and the denominator of the fraction 5/10 by the GCD, which is 5:
5 ÷ 5 = 1 10 ÷ 5 = 2
Step 4: Express the Simplified Fraction
This gives us the simplified fraction: 1/2
Therefore, 5/10 simplified to its lowest terms is 1/2.
Visualizing the Simplification: Using Diagrams
Visual aids can greatly enhance understanding. Imagine a pizza cut into 10 equal slices. The fraction 5/10 represents having 5 out of 10 slices. If we group the slices into pairs, we can see that 5 slices is equivalent to half the pizza (5/10 = 1/2). This visual representation makes the simplification process more intuitive.
Beyond 5/10: Simplifying Other Fractions
The process of simplifying fractions is consistent regardless of the numbers involved. Here's a general approach:
-
Find the GCD: Determine the greatest common divisor of the numerator and denominator. You can use prime factorization or the Euclidean algorithm for larger numbers.
-
Divide: Divide both the numerator and the denominator by the GCD.
-
Simplified Fraction: The result is the simplified fraction.
Example: Simplify 12/18
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
- GCD: The GCD of 12 and 18 is 6.
- Divide: 12 ÷ 6 = 2 and 18 ÷ 6 = 3
- Simplified Fraction: 12/18 simplifies to 2/3
Understanding Prime Factorization for GCD
For larger numbers, finding the GCD through simple factor listing can be cumbersome. Prime factorization provides a more efficient method. Prime factorization breaks down a number into its prime factors (numbers divisible only by 1 and themselves).
Example: Find the GCD of 24 and 36 using prime factorization.
- Prime Factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3
- Prime Factorization of 36: 2 x 2 x 3 x 3 = 2² x 3²
- GCD: The common factors are 2² and 3. Therefore, the GCD is 2² x 3 = 4 x 3 = 12.
Now, simplify the fraction 24/36 by dividing both the numerator and the denominator by the GCD (12):
24 ÷ 12 = 2 36 ÷ 12 = 3
So, 24/36 simplifies to 2/3.
The Euclidean Algorithm: An Alternative Method for GCD
The Euclidean algorithm is a more sophisticated method for finding the GCD, particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Example: Find the GCD of 48 and 18 using the Euclidean algorithm.
- Divide 48 by 18: 48 = 2 x 18 + 12 (Remainder is 12)
- Divide 18 by the remainder 12: 18 = 1 x 12 + 6 (Remainder is 6)
- Divide 12 by the remainder 6: 12 = 2 x 6 + 0 (Remainder is 0)
The last non-zero remainder is 6, so the GCD of 48 and 18 is 6.
Frequently Asked Questions (FAQ)
Q1: What if the numerator is larger than the denominator?
A1: Even if the numerator is larger than the denominator (an improper fraction), the simplification process remains the same. You still find the GCD and divide both the numerator and the denominator by it. The resulting fraction might still be improper, but it will be in its simplest form. For example, 15/10 simplifies to 3/2.
Q2: Can a fraction be simplified more than once?
A2: No. Once you've divided by the greatest common divisor, the fraction is in its simplest form. Any further division will result in a fraction that is no longer equivalent to the original.
Q3: Is there a quick way to tell if a fraction is already in its simplest form?
A3: If the numerator and the denominator have no common factors other than 1, the fraction is in its simplest form. In other words, if the GCD is 1, the fraction is already simplified.
Q4: Why is simplifying fractions important in real-world applications?
A4: Simplifying fractions is crucial for accuracy and clarity in various fields. In construction, precise measurements are essential; in cooking, accurate ingredient ratios are vital. In finance, simplifying fractions helps in understanding percentages and ratios. Generally, simplifying makes calculations easier and more manageable.
Conclusion: Mastering Fraction Simplification
Simplifying fractions, even seemingly simple ones like 5/10, is a fundamental skill in mathematics. Understanding the underlying principles of greatest common divisors and applying efficient methods like prime factorization or the Euclidean algorithm empowers you to tackle more complex fraction problems with confidence. By mastering fraction simplification, you're not only improving your mathematical abilities but also enhancing your problem-solving skills, skills applicable far beyond the classroom. Remember that consistent practice and a clear understanding of the concepts are key to mastering this essential skill. So, grab a pencil and paper, and start practicing! You'll be surprised how quickly you become proficient in simplifying fractions.
Latest Posts
Latest Posts
-
1 3 4 To Decimal
Sep 18, 2025
-
Is 7 8 Greater Than 5 8
Sep 18, 2025
-
What Percent Is 1 10
Sep 18, 2025
-
What Is 5 6 Of 3 4
Sep 18, 2025
-
17 Percent As A Fraction
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 10 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.