16/9 As A Mixed Number
saludintensiva
Sep 15, 2025 · 6 min read
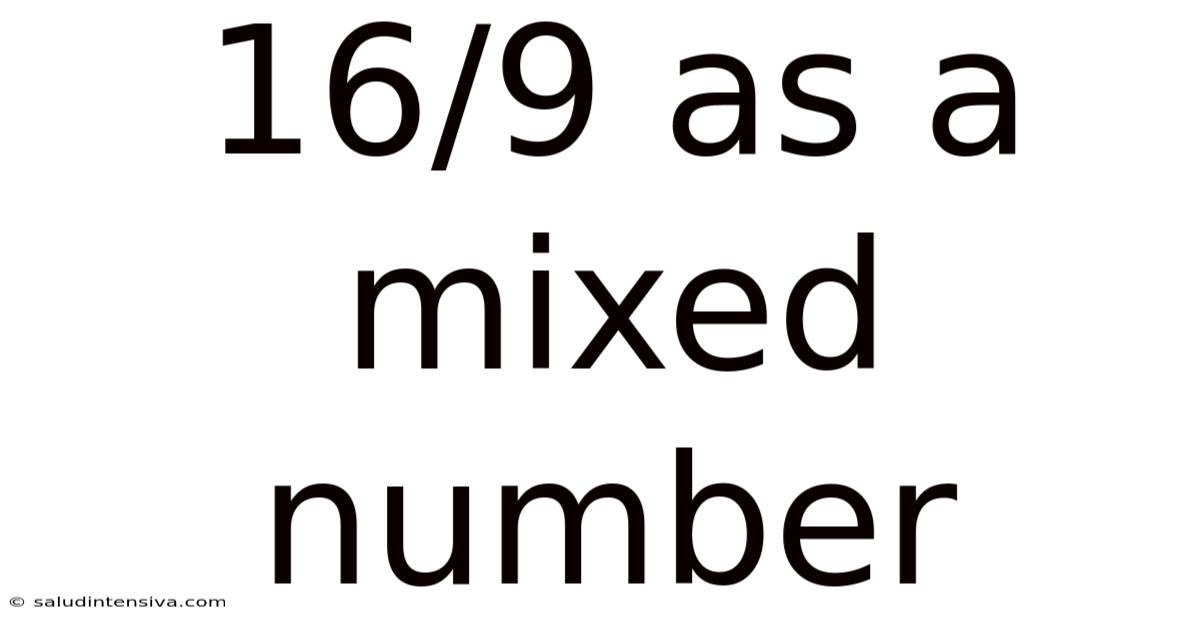
Table of Contents
Understanding 16/9 as a Mixed Number: A Comprehensive Guide
The seemingly simple fraction 16/9 holds a surprising depth when we explore its representation as a mixed number. This article will delve into the process of converting improper fractions like 16/9 into mixed numbers, providing a thorough understanding not just of the mechanics but also the underlying mathematical concepts. We'll explore various methods, address common misconceptions, and even delve into the practical applications of this conversion. This guide is designed for anyone looking to strengthen their understanding of fractions, from students brushing up on their math skills to adults seeking to improve their numeracy.
What is a Mixed Number?
Before we tackle the conversion of 16/9, let's define what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ½, 2 ¾, and 3 ⅛ are all mixed numbers. They represent a quantity greater than one whole unit.
Converting an Improper Fraction to a Mixed Number: The Basics
An improper fraction, unlike a proper fraction, has a numerator that is equal to or greater than the denominator. 16/9 is an improper fraction because 16 (the numerator) is larger than 9 (the denominator). Converting an improper fraction to a mixed number involves dividing the numerator by the denominator.
The process involves three simple steps:
-
Divide the numerator by the denominator: Divide 16 by 9. This gives us a quotient (the whole number part of the mixed number) and a remainder (the numerator of the fractional part). 16 ÷ 9 = 1 with a remainder of 7.
-
The quotient becomes the whole number part: The quotient, 1, becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the fraction: The remainder, 7, becomes the numerator of the fraction. The denominator remains the same as the original fraction's denominator, which is 9.
Therefore, 16/9 as a mixed number is 1 ⁷/₉.
Visualizing the Conversion: A Practical Approach
Imagine you have 16 pizzas, and you want to share them equally among 9 friends. You can give each friend one whole pizza (that's the quotient, 1). You'll have 7 slices left over (the remainder, 7). Since each pizza was originally divided into 9 slices, these 7 slices represent ⁷/₉ of a pizza. So, you have 1 whole pizza and ⁷/₉ of another pizza. This visually demonstrates why 16/9 is equivalent to 1 ⁷/₉.
Alternative Methods for Conversion
While the division method is straightforward, let's explore alternative approaches that can enhance understanding.
-
Repeated Subtraction: Subtract the denominator (9) repeatedly from the numerator (16) until the result is less than the denominator. This provides the same information as the division method, offering a different perspective.
16 - 9 = 7. We subtracted 9 once (our whole number), and the remainder (7) is less than 9. Thus, we have 1 ⁷/₉.
-
Using a Number Line: A number line can provide a visual representation of the conversion. You would start at zero and jump in increments of 9/9 (representing one whole). After one jump, you'll be at 9/9 or 1. You have 7/9 remaining to reach 16/9. This emphasizes the whole number aspect and the leftover fractional portion.
Common Mistakes to Avoid
Several common errors can occur during the conversion of improper fractions to mixed numbers:
-
Ignoring the Remainder: Forgetting to include the remainder as the numerator of the fractional part is a frequent mistake. Remember, the remainder represents the portion less than one whole.
-
Incorrect Denominator: Some students mistakenly change the denominator during the conversion. The denominator always remains the same as the original fraction's denominator.
-
Confusing Numerator and Denominator: Understanding the role of the numerator and denominator is crucial. The numerator represents the parts you have, and the denominator indicates the total number of parts in a whole.
Applying the Knowledge: Real-World Examples
Understanding the conversion of improper fractions to mixed numbers is not just an abstract mathematical exercise. It has practical applications in various real-world scenarios:
-
Measurement: When dealing with measurements (e.g., inches, centimeters), you might encounter improper fractions representing lengths. Converting them to mixed numbers makes these measurements easier to visualize and understand. For instance, 16/9 inches is equivalent to 1 ⁷/₉ inches.
-
Cooking and Baking: Recipes often involve fractions. If a recipe calls for 16/9 cups of flour, understanding that it's the same as 1 ⁷/₉ cups allows for easier measurement using standard measuring cups.
-
Data Representation: In various fields like statistics and data analysis, you might encounter improper fractions that represent proportions or ratios. Converting them to mixed numbers helps in representing these figures clearly and concisely.
-
Construction and Engineering: Precise measurements are essential. Converting an improper fraction to a mixed number will ensure that measurements are more easily understood and implemented in construction or engineering projects.
Further Exploration: Converting Mixed Numbers Back to Improper Fractions
It's important to also understand the reverse process: converting a mixed number back to an improper fraction. This involves:
-
Multiply the whole number by the denominator: In our example (1 ⁷/₉), multiply 1 by 9, which equals 9.
-
Add the numerator: Add the result (9) to the numerator (7), which equals 16.
-
Keep the denominator the same: The denominator remains 9.
Therefore, 1 ⁷/₉ converts back to the improper fraction 16/9. This demonstrates the equivalence between the two forms.
Frequently Asked Questions (FAQ)
Q1: Why do we need to convert improper fractions to mixed numbers?
A1: Converting to mixed numbers makes fractions easier to understand and visualize, especially in real-world situations where dealing with whole units and parts of units is common. It provides a more intuitive representation of quantities greater than one.
Q2: Can all improper fractions be converted to mixed numbers?
A2: Yes, all improper fractions can be converted to mixed numbers. The process of dividing the numerator by the denominator will always result in a whole number and a possible remainder.
Q3: What if the remainder is zero after dividing the numerator by the denominator?
A3: If the remainder is zero, it means the improper fraction is a whole number. For example, 18/9 = 2. There is no fractional part in this case.
Q4: Are there any shortcuts for converting improper fractions to mixed numbers?
A4: While the basic division method is always reliable, practicing mental arithmetic can help speed up the conversion process. Recognizing patterns and multiples of the denominator can contribute to efficiency.
Conclusion: Mastering the Art of Fraction Conversion
Converting improper fractions to mixed numbers is a fundamental skill in mathematics with wide-ranging applications. By understanding the underlying principles, employing various methods of conversion, and avoiding common pitfalls, you can confidently tackle these conversions and confidently apply this knowledge to real-world problems. This improved understanding will strengthen your mathematical foundation and empower you to solve a wider range of problems involving fractions. Remember to practice regularly to build your proficiency and increase your comfort level with this essential math concept. The seemingly simple task of converting 16/9 to 1 ⁷/₉ opens up a whole world of mathematical possibilities.
Latest Posts
Latest Posts
-
When Was 22 Weeks Ago
Sep 15, 2025
-
Present Value Of 1 Chart
Sep 15, 2025
-
Is 3 4 Greater Than 2 3
Sep 15, 2025
-
11 29 As A Percentage
Sep 15, 2025
-
2 13 As A Percentage
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 16/9 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.