16 Percent As A Fraction
saludintensiva
Sep 11, 2025 · 5 min read
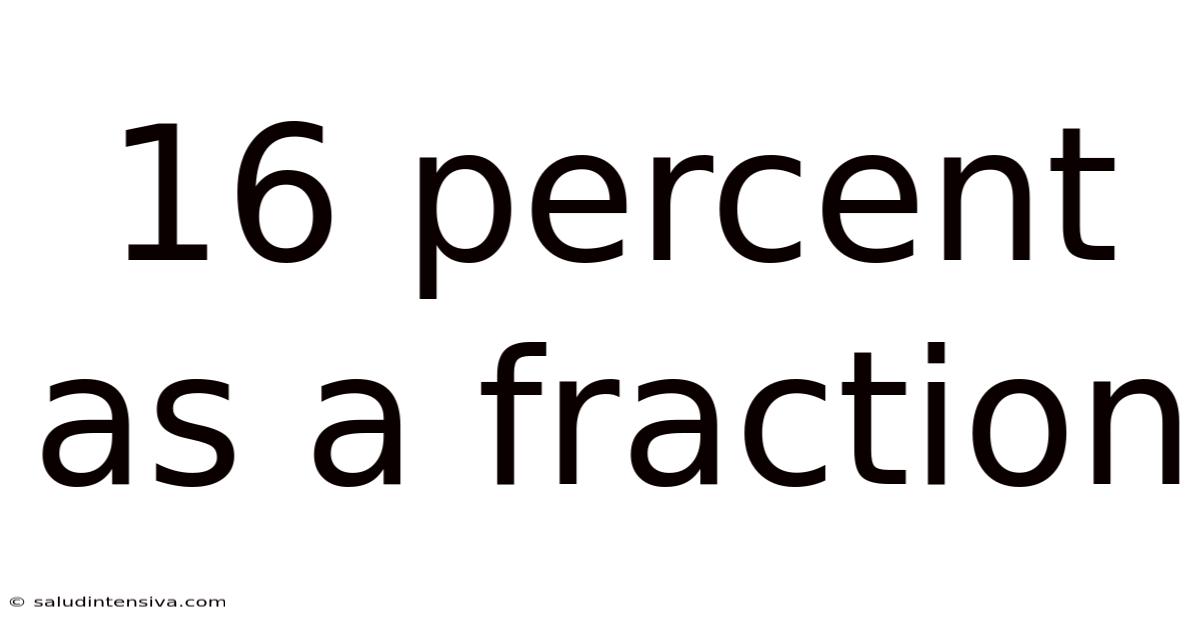
Table of Contents
Understanding 16 Percent as a Fraction: A Comprehensive Guide
Understanding percentages and their fractional equivalents is a fundamental skill in mathematics, crucial for various applications in daily life, from calculating discounts to understanding financial reports. This comprehensive guide delves into the intricacies of converting 16 percent into a fraction, exploring different methods, simplifying the fraction to its lowest terms, and expanding on the broader concept of percentage-to-fraction conversions. We'll also tackle common misconceptions and answer frequently asked questions, ensuring a solid understanding of this important mathematical concept.
From Percentage to Fraction: The Fundamental Conversion
The term "percent" literally means "out of one hundred." Therefore, any percentage can be directly expressed as a fraction with a denominator of 100. To convert 16 percent to a fraction, we simply write it as:
16/100
This fraction represents 16 parts out of a total of 100 parts. This is a straightforward and crucial first step in understanding how percentages translate to fractions.
Simplifying Fractions: Finding the Lowest Terms
While 16/100 accurately represents 16 percent, it's not in its simplest form. Simplifying a fraction means reducing it to its lowest terms by finding the greatest common divisor (GCD) of the numerator (16) and the denominator (100) and dividing both by it.
The GCD of 16 and 100 is 4. Dividing both the numerator and the denominator by 4, we get:
(16 ÷ 4) / (100 ÷ 4) = 4/25
Therefore, the simplest form of the fraction representing 16 percent is 4/25. This simplified fraction is equivalent to 16/100, but it's more concise and easier to work with in many mathematical operations.
Understanding the Concept of Equivalence
It's essential to understand that 16/100, 4/25, and 0.16 (the decimal equivalent) are all different representations of the same value. They represent the same proportion or ratio. Choosing the most appropriate representation often depends on the context of the problem. For instance, fractions are often preferred in situations requiring precise calculations or comparisons, while decimals are useful in calculations involving multiplication or division.
Visualizing 16 Percent as a Fraction
Visualizing fractions can significantly aid in understanding their value. Imagine a 10 x 10 grid, representing 100 squares. Shading 16 of these squares visually demonstrates 16/100, or 16 percent. Further, grouping these 16 squares into four groups of four highlights the simplified fraction 4/25, demonstrating that four out of every 25 squares are shaded. This visual representation reinforces the equivalence between different forms of the same value.
Real-World Applications of 16 Percent as a Fraction
Understanding how to convert 16 percent to a fraction has numerous practical applications:
-
Calculating Discounts: If an item is discounted by 16 percent, you can easily calculate the discount amount by multiplying the original price by 4/25. This fractional representation makes the calculation simpler than using the decimal equivalent in some cases.
-
Financial Calculations: In finance, understanding percentages and fractions is critical. Converting interest rates or profit margins to fractions can simplify complex calculations. For example, calculating compound interest often benefits from using fractional representations.
-
Probability and Statistics: Percentages and fractions are fundamental tools in probability and statistics. Expressing probabilities as fractions helps in calculating the likelihood of events occurring.
-
Measurement and Ratio: Many everyday situations involve ratios and proportions. Understanding 16 percent as 4/25 allows for easier comparison and calculations involving proportions. For instance, if a recipe calls for a certain proportion of ingredients, representing this proportion as a fraction can streamline calculations when scaling the recipe up or down.
Expanding on Percentage-to-Fraction Conversions: A General Approach
The conversion of 16 percent to a fraction is a specific example of a broader principle. Any percentage can be converted into a fraction by following these steps:
-
Write the percentage as a fraction with a denominator of 100. For example, x% becomes x/100.
-
Simplify the fraction. Find the greatest common divisor (GCD) of the numerator and the denominator and divide both by the GCD to obtain the simplest form of the fraction.
-
Check your work. Verify that the simplified fraction is equivalent to the original percentage by converting the fraction back into a percentage (multiplying the numerator by 100 and dividing by the denominator).
Dealing with Percentages Greater Than 100%
The method described above applies to percentages less than or equal to 100%. However, percentages greater than 100% are also possible and represent values greater than one. For example, 116% can be expressed as 116/100, which simplifies to 29/25 or 1 4/25. This indicates a value exceeding one whole unit.
Frequently Asked Questions (FAQs)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand and work with in calculations. It provides a more concise representation of the value and avoids unnecessary complexity in mathematical operations.
Q2: Can I convert a fraction back to a percentage?
A2: Yes, absolutely. To convert a fraction to a percentage, multiply the numerator by 100 and divide by the denominator. For example, to convert 4/25 back to a percentage, (4 x 100) / 25 = 16%, confirming that 4/25 is equivalent to 16%.
Q3: What if the percentage has a decimal component?
A3: If the percentage has a decimal component (e.g., 16.5%), follow the same steps but include the decimal in the numerator. For instance, 16.5% becomes 16.5/100, which simplifies to 33/200.
Q4: Are there any online calculators or tools to help with this conversion?
A4: While there are numerous online calculators available, understanding the underlying process of converting percentages to fractions is crucial for building a strong foundation in mathematics.
Conclusion: Mastering Percentages and Fractions
Converting 16 percent to a fraction, which simplifies to 4/25, is a fundamental skill in mathematics with wide-ranging applications. This guide provides a clear understanding of this conversion, highlighting its practical relevance and emphasizing the importance of simplifying fractions. By understanding the underlying principles and practicing the conversion process, you'll build a solid foundation in mathematics, paving the way for success in more complex mathematical applications. Remember, the ability to easily switch between percentages, fractions, and decimals empowers you to solve problems in various fields, from simple everyday calculations to advanced financial modeling. This understanding is not merely about memorizing formulas, but about grasping the fundamental concepts of ratio and proportion.
Latest Posts
Latest Posts
-
8 To The 4th Power
Sep 11, 2025
-
What Is 15 Of 100
Sep 11, 2025
-
13 500 As A Decimal
Sep 11, 2025
-
1 2 Minus 1 3
Sep 11, 2025
-
Convert 58 Pounds To Kilograms
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 16 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.