18 25 As A Percent
saludintensiva
Sep 13, 2025 · 5 min read
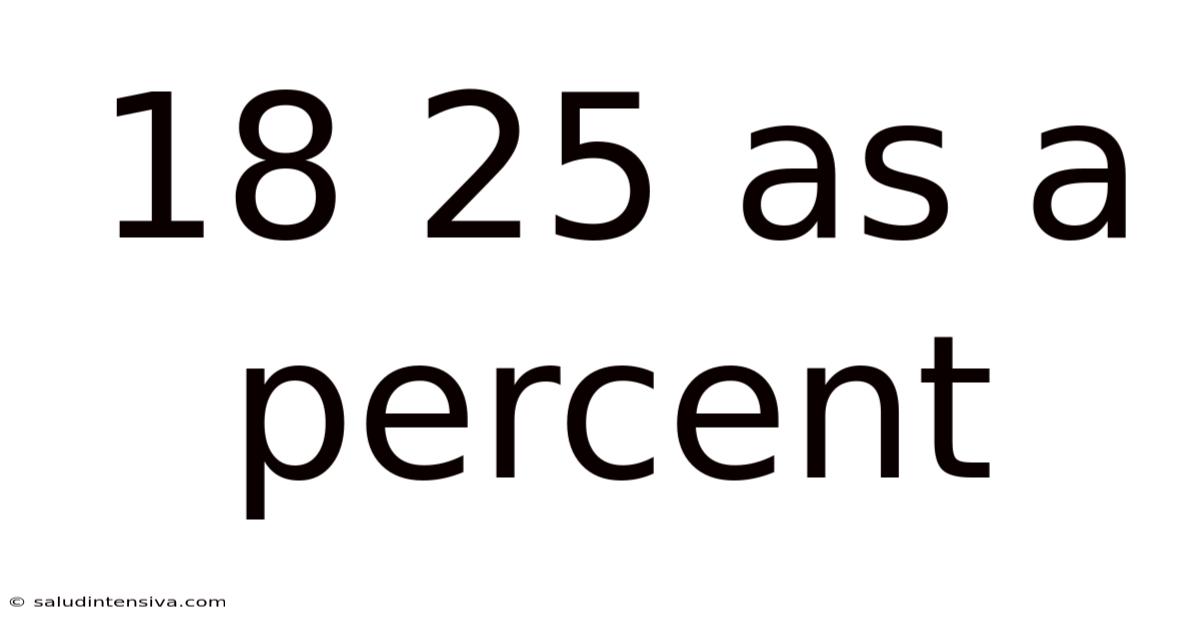
Table of Contents
18/25 as a Percent: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex scientific calculations. This article provides a comprehensive guide to calculating 18/25 as a percent, explaining the process step-by-step and exploring related concepts to build a solid foundation in percentage calculations. We'll cover the fundamental principles, delve into the practical application, and address frequently asked questions to ensure a complete understanding of this essential mathematical concept.
Understanding Percentages
A percentage represents a fraction of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of a hundred." Therefore, expressing a number as a percentage involves determining what proportion that number represents when the whole is considered as 100. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating 18/25 as a Percent: The Step-by-Step Approach
To convert the fraction 18/25 into a percentage, we follow these simple steps:
Step 1: Convert the Fraction to a Decimal
The first step is to transform the fraction 18/25 into its decimal equivalent. We achieve this by dividing the numerator (18) by the denominator (25):
18 ÷ 25 = 0.72
Step 2: Convert the Decimal to a Percentage
To convert the decimal 0.72 into a percentage, we multiply it by 100 and add the "%" symbol:
0.72 × 100 = 72%
Therefore, 18/25 is equal to 72%.
Alternative Method: Using Proportions
Another way to approach this problem is using proportions. We can set up a proportion where x represents the percentage we're trying to find:
18/25 = x/100
To solve for x, we cross-multiply:
25x = 1800
Then, we divide both sides by 25:
x = 1800 ÷ 25 = 72
So, again, we find that 18/25 is equal to 72%. This method reinforces the concept that a percentage is simply a fraction with a denominator of 100.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world situations. Here are some examples:
-
Financial Calculations: Calculating interest rates, discounts, taxes, profit margins, and tips all rely on percentage calculations. For instance, if a product is discounted by 20%, you'll need to calculate the discounted price using percentages.
-
Data Analysis: Percentages are widely used to represent data proportions in various contexts, like market share, survey results, and statistical analysis. For instance, if a survey shows 72% of respondents prefer a particular product, understanding percentage helps in interpreting the results.
-
Scientific Calculations: Percentages are used in scientific research and experiments to express changes, ratios, and concentrations. For instance, measuring the percentage of a certain element in a compound.
-
Everyday Life: We use percentages constantly in everyday life, from calculating sales tax to figuring out the percentage of a task completed. Understanding percentages makes these calculations quick and easy.
Further Exploring Percentage Concepts
Let's delve deeper into related concepts to solidify your understanding of percentages.
1. Percentage Increase and Decrease:
Calculating percentage increase or decrease involves determining the proportional change between two values. The formula for percentage change is:
[(New Value - Old Value) / Old Value] x 100%
For instance, if the price of an item increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100% = 20%
Similarly, if the price decreases from $60 to $50, the percentage decrease is:
[(50 - 60) / 60] x 100% = -16.67% (approximately)
2. Finding the Percentage of a Number:
To find a specific percentage of a number, you multiply the number by the percentage (expressed as a decimal). For example, finding 72% of 25:
0.72 x 25 = 18
This demonstrates the inverse relationship between the calculation we performed earlier.
3. Finding the Whole from a Percentage:
If you know a percentage and its corresponding value, you can calculate the whole. For example, if 72% of a number is 18, you can set up an equation:
0.72x = 18
Solving for x:
x = 18 / 0.72 = 25
This shows that 25 is the whole number, where 18 represents 72% of it.
Frequently Asked Questions (FAQ)
Q1: What if the fraction doesn't easily convert to a decimal?
A1: Some fractions might result in repeating decimals. In such cases, you can round the decimal to a certain number of decimal places for practical purposes. For example, 1/3 as a decimal is 0.3333... You might round it to 0.33 for most applications.
Q2: How do I convert a percentage back into a fraction?
A2: To convert a percentage to a fraction, divide the percentage by 100 and simplify the fraction. For example, 72% can be written as 72/100, which simplifies to 18/25.
Q3: Are there any online calculators to verify my percentage calculations?
A3: Yes, numerous online percentage calculators are available. These tools can help verify your manual calculations and assist in more complex percentage problems. However, understanding the underlying principles is crucial for applying percentage calculations effectively in diverse situations.
Q4: Why is understanding percentages important?
A4: Understanding percentages is crucial for various reasons, including financial literacy, data interpretation, and problem-solving in various fields. It allows for a better understanding of proportional relationships and enables effective decision-making in numerous real-world contexts.
Conclusion
Calculating 18/25 as a percent, which equals 72%, is a straightforward process involving converting the fraction to a decimal and then to a percentage. However, this article extends beyond a simple calculation, providing a comprehensive understanding of percentages, their application in various fields, and related concepts like percentage increase/decrease and finding the whole from a percentage. Mastering these concepts empowers you to confidently tackle percentage-related problems in diverse situations, strengthening your mathematical skills and improving your ability to analyze and interpret data effectively. Remember that practice is key to mastering percentage calculations. By consistently applying these principles and practicing various problems, you will develop a strong understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
9 Divided By 1 2
Sep 13, 2025
-
7 Out Of 13 Percentage
Sep 13, 2025
-
14 Acres In Square Feet
Sep 13, 2025
-
90 Days After August 15
Sep 13, 2025
-
5 6 Is Equivalent To
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 18 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.