9 Divided By 1 2
saludintensiva
Sep 13, 2025 · 5 min read
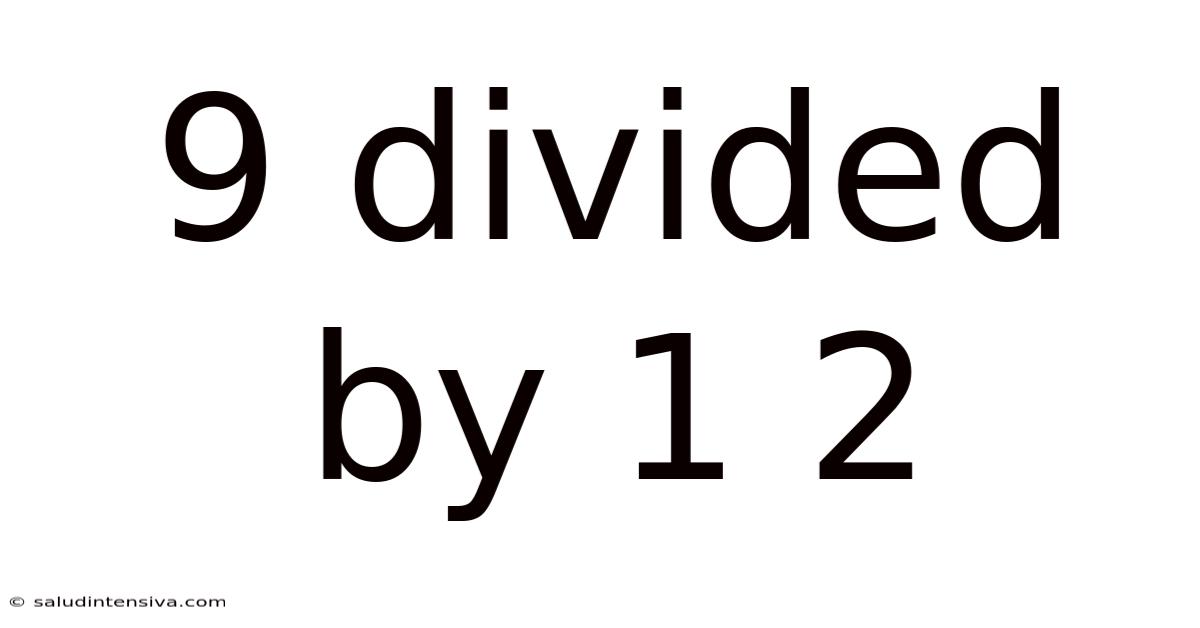
Table of Contents
Decoding 9 Divided by 1/2: A Deep Dive into Fractions and Division
Dividing by fractions can be a tricky concept for many, even for those comfortable with whole numbers. This article will thoroughly explore the seemingly simple problem of 9 divided by 1/2 (9 ÷ 1/2), explaining not only the solution but also the underlying mathematical principles and various approaches to solving it. Understanding this will build a strong foundation in fractional arithmetic, a crucial skill in mathematics and various real-world applications. We'll demystify the process, offering multiple perspectives to solidify your understanding.
Understanding the Fundamentals: Fractions and Division
Before diving into the specific problem, let's refresh our understanding of fractions and division.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, 1/2 represents one out of two equal parts, or one-half.
Division, in its simplest form, is the process of splitting a quantity into equal parts. When we divide 9 by 3, we're asking, "How many groups of 3 are there in 9?" The answer, of course, is 3. But when dealing with fractions, the concept remains the same, though the method may seem different.
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This is perhaps the most common and straightforward method for dividing fractions. It relies on the concept of reciprocals. The reciprocal of a fraction is obtained by swapping the numerator and denominator. For example, the reciprocal of 1/2 is 2/1 (or simply 2).
Here's how to apply this method to solve 9 ÷ 1/2:
- Keep: Keep the first number (dividend) as it is: 9.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second number (divisor) – find its reciprocal. The reciprocal of 1/2 is 2/1 or 2.
- Multiply: Multiply the first number by the reciprocal of the second number: 9 × 2 = 18.
Therefore, 9 ÷ 1/2 = 18.
Method 2: Visual Representation
Visualizing the problem can make it more intuitive. Imagine you have 9 pizzas, and you want to divide each pizza into halves (1/2). How many halves would you have in total?
Each pizza yields 2 halves (2/2 = 1 whole pizza). Since you have 9 pizzas, you'll have 9 × 2 = 18 halves. This visually demonstrates why 9 ÷ 1/2 = 18.
Method 3: Understanding Division as Repeated Subtraction
Another way to interpret division is as repeated subtraction. How many times can you subtract 1/2 from 9? While you wouldn't typically perform repeated subtraction with fractions in this manner (it would be tedious), it helps to conceptualize the division process. You can subtract 1/2 from 9 eighteen times before you reach zero, reinforcing the answer of 18.
Method 4: Converting to Improper Fractions
This method involves converting whole numbers into improper fractions before performing the division.
- Convert the whole number: Convert 9 into a fraction with a denominator of 1: 9/1.
- Divide the fractions: Now you have 9/1 ÷ 1/2.
- Apply the reciprocal method: Keep 9/1, change ÷ to ×, and flip 1/2 to 2/1. This gives (9/1) × (2/1).
- Multiply the numerators and denominators: (9 × 2) / (1 × 1) = 18/1 = 18.
This method showcases the consistency of the reciprocal method when dealing with mixed fractions and whole numbers.
The Mathematical Rationale: Why Does "Keep, Change, Flip" Work?
The "Keep, Change, Flip" method isn't just a trick; it's a consequence of the properties of fractions and division. Remember that dividing by a fraction is the same as multiplying by its reciprocal. This can be proven using the concept of multiplicative inverses.
The multiplicative inverse (or reciprocal) of a number is the number that, when multiplied by the original number, results in 1. For instance, the multiplicative inverse of 1/2 is 2 because (1/2) × 2 = 1.
When we divide by a fraction (a/b), we are essentially multiplying by its reciprocal (b/a). This is because division is the inverse operation of multiplication. Therefore, 9 ÷ (1/2) is equivalent to 9 × (2/1), which simplifies to 18.
Real-World Applications
Understanding division with fractions isn't just an academic exercise; it has numerous real-world applications. Consider these examples:
- Baking: If a recipe calls for 1/2 cup of sugar per serving, and you want to make 9 servings, you'll need 9 ÷ (1/2) = 9 cups of sugar.
- Sewing: If you need 1/2 yard of fabric for each project, and you have 9 yards, you can make 18 projects.
- Construction: If a task requires 1/2 hour of labor, and you have 9 hours available, you can complete 18 tasks.
Frequently Asked Questions (FAQs)
Q: Can I use a calculator to solve this problem?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for problem-solving beyond simple calculations.
Q: What if the problem was 1/2 divided by 9?
A: The process remains the same. You would keep 1/2, change the division sign to multiplication, and flip 9 (which is 9/1) to 1/9. The result would be (1/2) × (1/9) = 1/18.
Q: What if the numbers were more complex fractions?
A: The "Keep, Change, Flip" method works equally well with complex fractions. Simply find the reciprocal of the divisor and multiply.
Conclusion: Mastering Fractional Division
Mastering the division of fractions, as exemplified by the problem 9 divided by 1/2, is a fundamental skill in mathematics. This article has explored multiple approaches, from the efficient "Keep, Change, Flip" method to visual representations and the underlying mathematical rationale. By understanding these methods, you not only solve the problem but also develop a deeper understanding of fractions, division, and their interrelationship. This foundational knowledge is invaluable not only for further mathematical studies but also for navigating various real-world situations where fractional arithmetic is necessary. Remember to practice regularly to build confidence and fluency in working with fractions. The more you practice, the easier and more intuitive these concepts will become.
Latest Posts
Latest Posts
-
Lcm Of 24 And 21
Sep 13, 2025
-
2 To The 3 Power
Sep 13, 2025
-
What Time Is 21 40
Sep 13, 2025
-
27 Out Of 30 Percentage
Sep 13, 2025
-
1 3 Divided By 4
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 9 Divided By 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.