Lcm Of 24 And 21
saludintensiva
Sep 13, 2025 · 5 min read
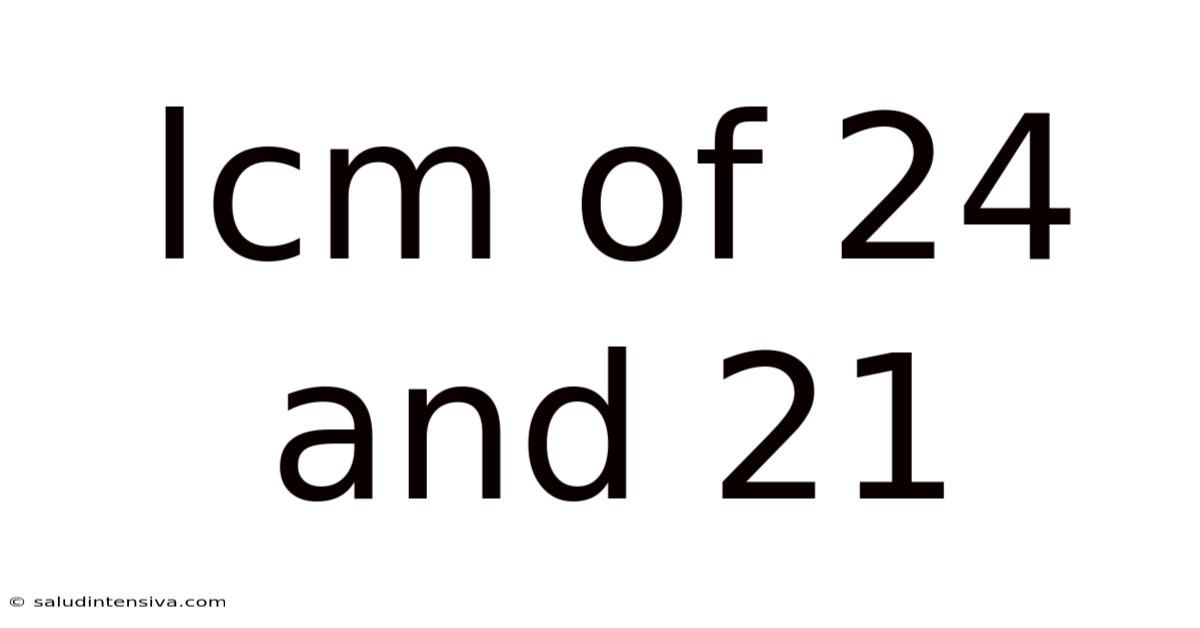
Table of Contents
Finding the Least Common Multiple (LCM) of 24 and 21: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation provides a deeper appreciation of number theory. This comprehensive guide will explore the LCM of 24 and 21, detailing multiple approaches, explaining the mathematical principles involved, and answering frequently asked questions. We'll move beyond simply finding the answer and delve into why this calculation is important in various mathematical and real-world applications.
Introduction: Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers you're considering as factors. Understanding LCM is crucial in various mathematical contexts, from simplifying fractions to solving problems involving cycles and periodic events. This guide will focus on finding the LCM of 24 and 21, illustrating multiple methods to achieve this.
Method 1: Listing Multiples
This is a straightforward method, especially useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240, 264, 288, 312, 336…
- Multiples of 21: 21, 42, 63, 84, 105, 126, 147, 168, 189, 210, 231, 252…
By comparing the lists, we see that the smallest number present in both lists is 168. Therefore, the LCM of 24 and 21 is 168. While simple for smaller numbers, this method becomes less practical for larger numbers.
Method 2: Prime Factorization
This method uses the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
-
Prime Factorization of 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3¹
-
Prime Factorization of 21: 21 = 3 x 7 = 3¹ x 7¹
-
Finding the LCM: To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations and multiply them together.
- The prime factors are 2, 3, and 7.
- The highest power of 2 is 2³.
- The highest power of 3 is 3¹.
- The highest power of 7 is 7¹.
Therefore, LCM(24, 21) = 2³ x 3¹ x 7¹ = 8 x 3 x 7 = 168.
This method is more efficient than listing multiples, particularly for larger numbers, as it systematically considers all prime factors.
Method 3: Using the Greatest Common Divisor (GCD)
The greatest common divisor (GCD) is the largest positive integer that divides both numbers without leaving a remainder. There's a relationship between LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
-
Finding the GCD of 24 and 21: We can use the Euclidean algorithm to find the GCD.
- 24 = 21 x 1 + 3
- 21 = 3 x 7 + 0
The last non-zero remainder is 3, so GCD(24, 21) = 3.
-
Calculating the LCM: Using the formula:
LCM(24, 21) = (24 x 21) / GCD(24, 21) = (24 x 21) / 3 = 504 / 3 = 168.
This method is efficient because finding the GCD is often faster than directly calculating the LCM, especially for larger numbers. The Euclidean algorithm provides a systematic way to find the GCD.
Method 4: Using a Least Common Multiple Calculator (for verification)
While not a method for calculating the LCM manually, using an online calculator can serve as a valuable tool to verify your calculations. Many free online calculators are available, which can provide quick results and offer an independent check to ensure accuracy. Remember to double-check the input values for accuracy.
The Significance of LCM in Real-World Applications
The concept of LCM extends beyond abstract mathematical exercises. It has practical applications in various fields:
-
Scheduling: Imagine two buses depart from the same station at different intervals. The LCM helps determine when they'll depart together again. This concept applies to various scheduling problems, from production lines to appointment timings.
-
Fraction Operations: When adding or subtracting fractions, finding the LCM of the denominators is crucial for obtaining a common denominator. This simplifies the process and allows for accurate calculations.
-
Cyclic Events: Problems involving periodic events, such as planetary orbits or repeating patterns in nature, often require the use of LCM to determine when certain events will coincide.
-
Music Theory: In music, the LCM is used to determine the least common denominator for time signatures, leading to harmonious rhythms and consistent musical structures.
Frequently Asked Questions (FAQ)
-
What if the two numbers are coprime (their GCD is 1)? If the GCD of two numbers is 1, then their LCM is simply the product of the two numbers. For example, LCM(5, 7) = 35.
-
Can the LCM of two numbers be smaller than the larger number? No, the LCM of two numbers is always greater than or equal to the larger of the two numbers.
-
What is the LCM of more than two numbers? To find the LCM of more than two numbers, you can extend the prime factorization method or use iterative application of the two-number LCM calculation.
Conclusion: Mastering LCM Calculations
Finding the least common multiple is a fundamental skill in mathematics with practical applications in various fields. We've explored four different methods for calculating the LCM of 24 and 21, each with its own advantages and disadvantages. Understanding these methods provides a deeper insight into number theory and enhances your problem-solving abilities. Remember, the choice of method depends on the context and the size of the numbers involved. While calculators can be helpful, mastering the underlying principles ensures a strong foundation in mathematical concepts. The ability to calculate the LCM efficiently and accurately is a valuable asset in both academic and real-world scenarios. This comprehensive understanding equips you to tackle more complex problems involving multiples and divisors with confidence.
Latest Posts
Latest Posts
-
Convert Psi To L Min
Sep 13, 2025
-
Gcf Of 8 And 18
Sep 13, 2025
-
2 The Power Of 8
Sep 13, 2025
-
Four And A Half Inch
Sep 13, 2025
-
Lcm Of 3 And 15
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 24 And 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.