Lcm Of 3 And 15
saludintensiva
Sep 13, 2025 · 6 min read
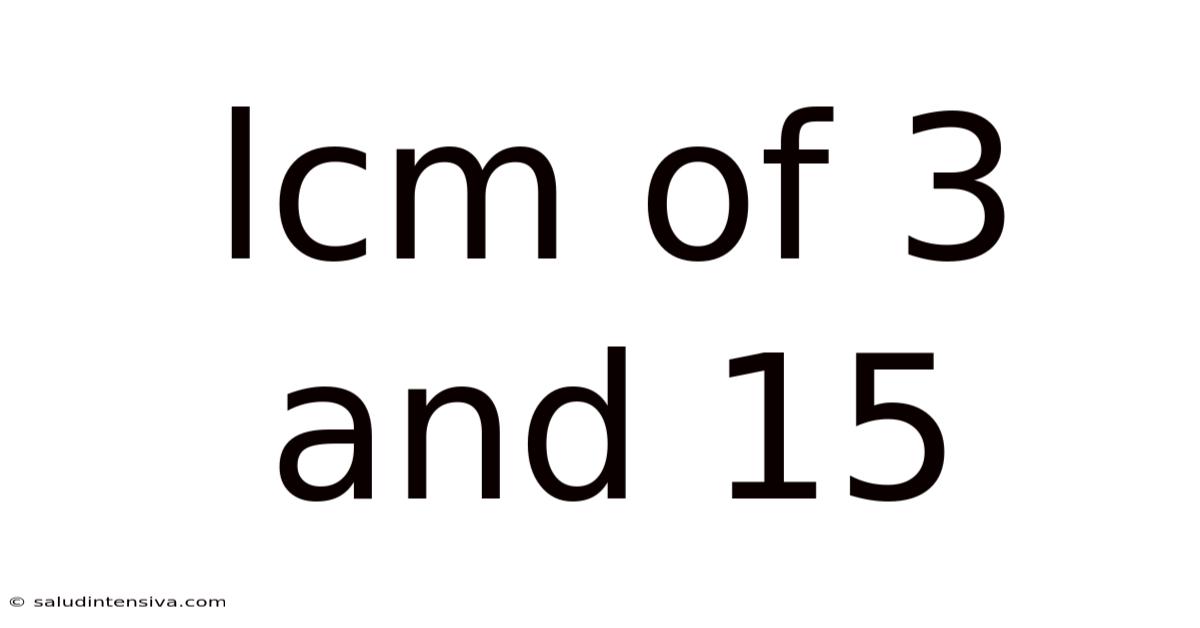
Table of Contents
Understanding the Least Common Multiple (LCM) of 3 and 15: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in arithmetic, algebra, and even more advanced areas like number theory. This comprehensive guide will delve into the LCM of 3 and 15, explaining not only how to calculate it but also exploring the underlying principles and applications of LCM. Understanding LCM goes beyond simple calculations; it provides a deeper understanding of number relationships and lays the groundwork for more complex mathematical concepts. This article will cover various methods for finding the LCM, explain the theoretical basis behind it, and provide illustrative examples to solidify your understanding.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…
The common multiples of 2 and 3 are 6, 12, 18, 24, and so on. The smallest of these common multiples is 6; therefore, the LCM of 2 and 3 is 6.
Calculating the LCM of 3 and 15: Various Methods
Now, let's focus on calculating the LCM of 3 and 15. We'll explore several methods to determine the LCM, each providing a unique approach and enhancing our understanding of the concept.
1. Listing Multiples Method:
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21…
- Multiples of 15: 15, 30, 45, 60…
As you can see, the smallest common multiple of 3 and 15 is 15. Therefore, the LCM(3, 15) = 15.
2. Prime Factorization Method:
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 15: 3 x 5
The LCM is found by taking the highest power of each prime factor present in the factorizations. In this case, we have:
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Therefore, the LCM(3, 15) = 3 x 5 = 15.
3. Greatest Common Divisor (GCD) Method:
The LCM and GCD (greatest common divisor) of two numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This is expressed as:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 3 and 15 using the Euclidean algorithm:
- Divide the larger number (15) by the smaller number (3): 15 ÷ 3 = 5 with a remainder of 0.
- Since the remainder is 0, the GCD is the smaller number, which is 3.
Now, we can use the formula:
LCM(3, 15) x GCD(3, 15) = 3 x 15
LCM(3, 15) x 3 = 45
LCM(3, 15) = 45 ÷ 3 = 15
Therefore, the LCM(3, 15) = 15.
Understanding the Relationship Between LCM and GCD
The relationship between the LCM and GCD is a fundamental concept in number theory. The formula LCM(a, b) * GCD(a, b) = a * b highlights the interconnectedness between these two values. Understanding this relationship provides a powerful tool for solving problems involving both LCM and GCD. It also allows for the calculation of one if the other is known. This is particularly useful when dealing with larger numbers where finding the prime factorization might be more complex.
Applications of LCM
The concept of LCM finds applications in various areas, including:
-
Fraction Arithmetic: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to find a common denominator. This simplifies the process significantly. For example, to add 1/3 and 1/15, finding the LCM (15) allows us to rewrite the fractions as 5/15 and 1/15, resulting in a sum of 6/15 which simplifies to 2/5.
-
Scheduling Problems: LCM is useful in solving scheduling problems where events repeat at different intervals. For example, if two buses leave a station at intervals of 3 and 15 minutes respectively, the LCM (15 minutes) determines when both buses will depart simultaneously again.
-
Pattern Recognition: In number patterns and sequences, the LCM can help predict when certain patterns will repeat or coincide.
Why is LCM Important?
The importance of understanding LCM extends beyond its immediate applications. It reinforces fundamental concepts like divisibility, prime factorization, and the relationships between numbers. Mastering LCM lays a crucial foundation for more advanced mathematical concepts encountered in algebra, number theory, and other branches of mathematics. The ability to efficiently calculate the LCM is essential for solving various problems in these fields.
Frequently Asked Questions (FAQ)
Q1: Is the LCM always larger than the numbers involved?
A1: No, the LCM can be equal to the largest number involved, as seen in the case of LCM(3, 15) = 15. This occurs when one number is a multiple of the other.
Q2: What if I have more than two numbers? How do I find the LCM?
A2: The methods we discussed can be extended to more than two numbers. For the prime factorization method, you would consider all prime factors and take the highest power of each. For the GCD method, you'd need to apply it iteratively. For example, for LCM(2, 3, 6), the prime factorization method is easiest: 2¹ * 3¹ = 6.
Q3: Can I use a calculator to find the LCM?
A3: Yes, many scientific calculators and online calculators have built-in functions to calculate the LCM of two or more numbers. However, understanding the underlying methods remains crucial for problem-solving and grasping the mathematical principles involved.
Q4: What is the difference between LCM and GCF (Greatest Common Factor)?
A4: The LCM is the smallest common multiple, while the GCF (also known as GCD, Greatest Common Divisor) is the largest common factor. They represent opposite ends of the spectrum of commonalities between two numbers. The LCM focuses on multiples, while the GCF focuses on factors.
Q5: Are there any shortcuts for finding the LCM?
A5: If one number is a multiple of the other, the LCM is simply the larger number. Using the prime factorization method can be efficient, especially when dealing with larger numbers, as it avoids the sometimes tedious process of listing multiples. Understanding the relationship between LCM and GCD provides a powerful alternative method, too.
Conclusion
The LCM of 3 and 15 is 15. This seemingly simple calculation highlights a fundamental concept with far-reaching implications in mathematics. By exploring different methods of calculation and understanding the theoretical underpinnings, we gain a deeper appreciation for the significance of the least common multiple. Its applications extend beyond basic arithmetic, playing a vital role in various areas of mathematics and problem-solving. This comprehensive guide aims to provide a solid foundation for understanding and applying the LCM concept effectively. The ability to calculate and understand LCM is a valuable skill, enhancing mathematical proficiency and problem-solving capabilities in numerous contexts.
Latest Posts
Latest Posts
-
Completing The Square Practice Problems
Sep 13, 2025
-
16666 Repeating As A Fraction
Sep 13, 2025
-
90 Degrees C To F
Sep 13, 2025
-
Lcm Of 14 And 49
Sep 13, 2025
-
58 Minutes Ago From Now
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.