18 Percent As A Fraction
saludintensiva
Sep 15, 2025 · 5 min read
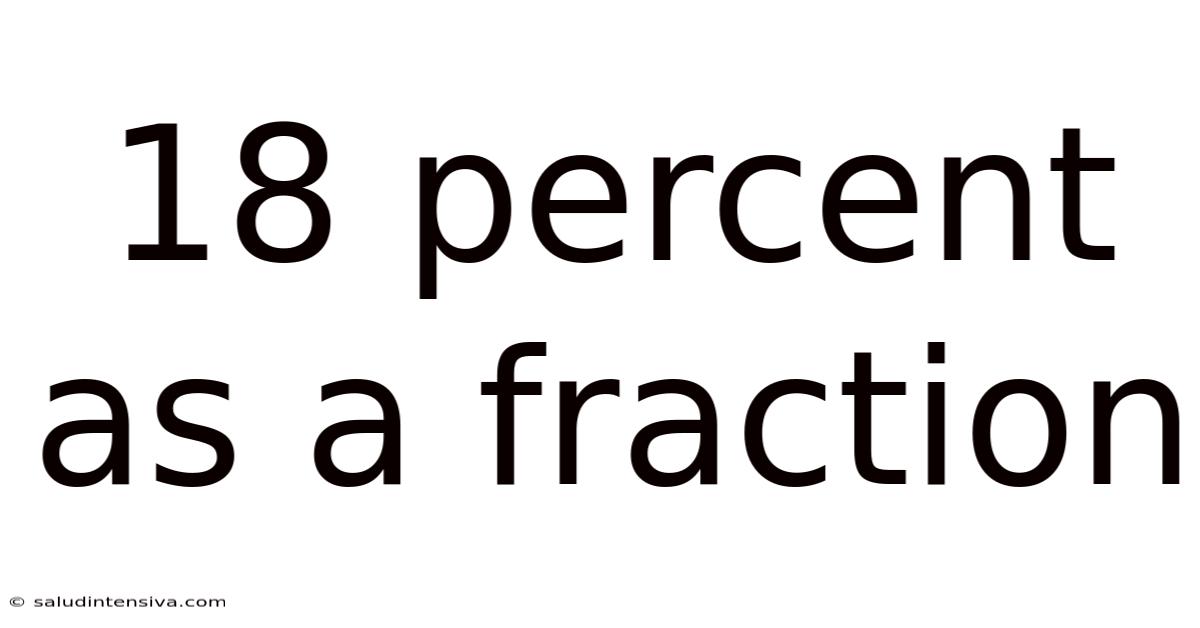
Table of Contents
Understanding 18 Percent as a Fraction: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to comprehending statistics and financial data. This article delves into the conversion of percentages to fractions, specifically focusing on how to express 18 percent as a fraction in its simplest form. We'll explore the process step-by-step, explain the underlying mathematical principles, and address frequently asked questions. By the end, you'll not only know how to represent 18% as a fraction but also gain a deeper understanding of percentage-fraction conversions.
From Percentage to Fraction: A Step-by-Step Guide
The term "percent" literally means "per hundred" (per centum in Latin). Therefore, any percentage can be easily converted to a fraction by writing the percentage number as the numerator and 100 as the denominator. Let's apply this to 18%:
-
Write the percentage as a fraction: 18% can be written as the fraction 18/100. This directly represents 18 parts out of a total of 100 parts.
-
Simplify the fraction: The fraction 18/100 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of both the numerator (18) and the denominator (100). The GCD is the largest number that divides both 18 and 100 without leaving a remainder.
The factors of 18 are 1, 2, 3, 6, 9, and 18. The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100.
The greatest common factor of 18 and 100 is 2.
-
Divide both the numerator and the denominator by the GCD: Divide both 18 and 100 by 2:
18 ÷ 2 = 9 100 ÷ 2 = 50
Therefore, 18% simplified as a fraction is 9/50.
This fraction, 9/50, represents the same value as 18/100 but is expressed in its simplest form. This means there's no other whole number that can divide both the numerator and denominator evenly.
Understanding the Mathematical Principles
The conversion from percentage to fraction hinges on the fundamental concept of ratio and proportion. A percentage expresses a ratio as a proportion of 100. For example, 18% indicates a ratio of 18 to 100. This ratio can then be expressed as a fraction: 18/100. Simplifying the fraction merely reduces the ratio to its simplest equivalent form without altering its value.
This principle applies to any percentage. To convert any percentage to a fraction, follow these steps:
- Write the percentage as a fraction with 100 as the denominator.
- Simplify the fraction by dividing both the numerator and denominator by their greatest common divisor.
Working with Different Percentages: Examples
Let's apply this process to a few more examples to solidify your understanding:
-
25%: 25/100. The GCD of 25 and 100 is 25. 25 ÷ 25 = 1 and 100 ÷ 25 = 4. Therefore, 25% = 1/4.
-
50%: 50/100. The GCD of 50 and 100 is 50. 50 ÷ 50 = 1 and 100 ÷ 50 = 2. Therefore, 50% = 1/2.
-
75%: 75/100. The GCD of 75 and 100 is 25. 75 ÷ 25 = 3 and 100 ÷ 25 = 4. Therefore, 75% = 3/4.
-
60%: 60/100. The GCD of 60 and 100 is 20. 60 ÷ 20 = 3 and 100 ÷ 20 = 5. Therefore, 60% = 3/5.
Beyond Simple Fractions: Handling Decimals
Sometimes, simplifying a fraction results in a decimal in the numerator or denominator. For instance, let's consider 12.5%:
-
Write as a fraction: 12.5/100
-
Remove the decimal: Multiply both the numerator and denominator by 10 to remove the decimal: 125/1000
-
Simplify: The GCD of 125 and 1000 is 125. 125 ÷ 125 = 1 and 1000 ÷ 125 = 8. Therefore, 12.5% = 1/8.
This demonstrates that even with decimal percentages, the fundamental principle of finding the GCD remains crucial for simplifying the resulting fraction.
Real-World Applications of Percentage to Fraction Conversions
The ability to convert percentages to fractions is essential in numerous real-world scenarios:
-
Cooking and Baking: Recipes often use percentages to indicate the proportion of ingredients. Converting these percentages to fractions allows for more precise measurements.
-
Finance: Understanding interest rates, discounts, and tax calculations often involves converting percentages to fractions to perform accurate calculations.
-
Science and Engineering: Many scientific and engineering applications utilize percentages to represent data and proportions. Converting these percentages to fractions can be necessary for various calculations and analyses.
-
Data Analysis and Statistics: Presenting data in fractional form can sometimes offer a clearer representation of proportions compared to percentages.
Frequently Asked Questions (FAQ)
Q: What if the fraction cannot be simplified further?
A: If the numerator and denominator share no common factors other than 1, the fraction is already in its simplest form. For example, 17% is 17/100, which cannot be simplified further.
Q: Can I convert a fraction back to a percentage?
A: Yes, absolutely! To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100%. For example, 9/50 = (9 ÷ 50) × 100% = 0.18 × 100% = 18%.
Q: Are there any shortcuts for simplifying fractions?
A: While finding the GCD is the most reliable method, you can sometimes spot common factors quickly. For instance, if both the numerator and denominator are even numbers, you can immediately divide by 2. If they both end in 0 or 5, they are divisible by 5.
Conclusion: Mastering Percentage-Fraction Conversions
Converting percentages to fractions, like transforming 18% into 9/50, is a crucial skill applicable across various fields. This process, while seemingly simple, underlies a deeper understanding of ratios, proportions, and mathematical simplification. By mastering this conversion, you equip yourself with a powerful tool for solving problems, analyzing data, and navigating the quantitative aspects of daily life. Remember the steps: write the percentage as a fraction over 100, find the greatest common divisor, and simplify the fraction. With practice, you'll confidently handle any percentage-to-fraction conversion, including more complex examples with decimals.
Latest Posts
Latest Posts
-
2 10 As A Decimal
Sep 15, 2025
-
12 6 As A Mixed Number
Sep 15, 2025
-
3 5 In Decimal Form
Sep 15, 2025
-
42 9 As A Decimal
Sep 15, 2025
-
13 6 As A Decimal
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 18 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.