2 3 5 9 Simplify
saludintensiva
Sep 13, 2025 · 5 min read
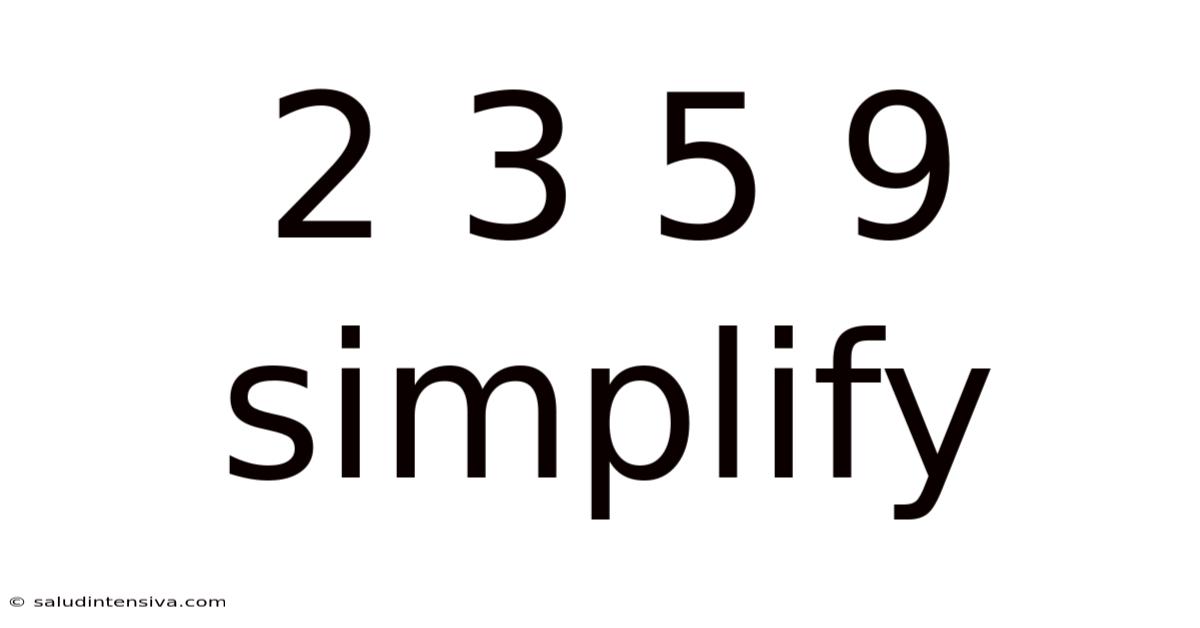
Table of Contents
Decoding the Mystery: Simplifying the Sequence 2, 3, 5, 9
The seemingly simple sequence 2, 3, 5, 9… often presents a fascinating puzzle. At first glance, it might appear random. However, a deeper dive reveals multiple possible approaches to understanding and continuing this sequence, highlighting the beauty of mathematical ambiguity and the power of pattern recognition. This article will explore various methods to simplify and understand this sequence, catering to readers of all mathematical backgrounds, from beginners to those with more advanced knowledge. We will delve into the different interpretations, demonstrate the underlying logic, and address frequently asked questions. By the end, you'll not only understand how to simplify this specific sequence but also develop a stronger grasp of mathematical reasoning and pattern identification.
Understanding the Challenge: What Does "Simplify" Mean?
Before we begin, it's crucial to define what "simplifying" means in this context. It doesn't imply finding a single, universally accepted "correct" answer. Instead, it means identifying the underlying pattern or rule that governs the sequence and expressing it in a concise and understandable form. This could involve:
- Finding a mathematical formula: A formula that generates each term in the sequence based on its position.
- Identifying a recursive relationship: A rule that defines each term based on the preceding term(s).
- Recognizing a pattern based on operations: Identifying a consistent mathematical operation (addition, subtraction, multiplication, division, etc.) or combination of operations that transforms one term into the next.
Method 1: Analyzing Differences Between Consecutive Terms
One common approach is to examine the differences between consecutive terms. Let's calculate the differences:
- 3 - 2 = 1
- 5 - 3 = 2
- 9 - 5 = 4
Notice a pattern? The differences themselves form a sequence: 1, 2, 4... This suggests that the differences are powers of 2: 2⁰, 2¹, 2². If we continue this pattern, the next difference would be 2³ = 8. Therefore, the next term in the original sequence would be 9 + 8 = 17. This approach leads to the sequence: 2, 3, 5, 9, 17, 33, 65, 129...
This method gives us a recursive relationship: a<sub>n+1</sub> = a<sub>n</sub> + 2<sup>n-1</sup>, where a<sub>1</sub> = 2. This formula allows us to generate any term in the sequence.
Method 2: Exploring a Potential Summation Pattern
Another approach involves looking at the sequence as a sum of terms. We can express each term as a sum of powers of 2:
- 2 = 2¹
- 3 = 2¹ + 2⁰
- 5 = 2² + 2⁰
- 9 = 2³ + 2⁰
Note that the powers of 2 are increasing, and we always add 2⁰ (which is 1). We could interpret this as a sum of an increasing power of 2 and a constant value of 1. Following this pattern, the next term would be:
- 2⁴ + 2⁰ = 16 + 1 = 17
This again yields the sequence 2, 3, 5, 9, 17... This approach, while seemingly different, leads to the same result as Method 1, demonstrating the interconnectedness of mathematical concepts.
Method 3: Considering a Combination of Operations
A more nuanced approach might involve a combination of operations. Let's analyze the sequence again:
- 2
- 2 + 1 = 3
- 3 + 2 = 5
- 5 + 4 = 9
We see a pattern emerging where we add successive powers of 2 to the previous term. This mirrors Method 1 and reinforces the finding that the next term is 17. This approach highlights the flexibility of mathematical thinking – multiple paths can lead to the same solution.
Method 4: Introducing a More Complex Pattern (Optional)
While the previous methods provide a satisfactory explanation, it's important to acknowledge that other, more complex patterns might exist. Mathematics is full of surprising relationships. For example, one could potentially introduce a more sophisticated pattern that initially aligns with 2, 3, 5, 9 but diverges later. This underscores the inherent ambiguity in extending a finite sequence. Without further terms, there's no definitive way to completely rule out more complex possibilities. However, simpler explanations are generally preferred in the absence of contradicting evidence.
The Importance of Context: Why Multiple Solutions Matter
The fact that multiple plausible solutions exist for simplifying the sequence 2, 3, 5, 9 highlights a crucial point: mathematical problems often have multiple valid interpretations. There isn't always a single "right" answer. The process of exploring these different approaches and evaluating their plausibility is just as important as finding a particular solution. This fosters critical thinking and enhances problem-solving skills.
Frequently Asked Questions (FAQ)
-
Q: Is there only one correct way to simplify this sequence?
- A: No, as shown above, several valid methods lead to different but equally plausible continuations of the sequence. The "correctness" depends on the underlying assumptions and the chosen interpretation of the pattern.
-
Q: Can this sequence be represented by a closed-form formula (non-recursive)?
- A: While a recursive formula is easily derived (as shown in Method 1), finding a simple, direct closed-form formula might be more challenging. It would require a deeper understanding of the underlying mathematical structure, potentially involving techniques from advanced number theory.
-
Q: How can I improve my ability to identify patterns in sequences?
- A: Practice is key! Work through various sequence problems, experimenting with different approaches – calculating differences, looking for sums, considering combinations of operations. The more you practice, the better you become at recognizing patterns and formulating mathematical relationships.
-
Q: What if the sequence was different? How would I approach it?
- A: The strategies outlined here – analyzing differences, examining sums, and looking for combinations of operations – are generally applicable to many sequences. The key is to systematically explore different possibilities and test whether a proposed pattern holds true for all given terms.
Conclusion: Embracing Mathematical Exploration
Simplifying the sequence 2, 3, 5, 9 isn't just about finding a single answer; it's about the journey of mathematical exploration. The multiple solutions highlight the rich possibilities within seemingly simple patterns. The methods explored here – analyzing differences, examining sums, and investigating combined operations – are valuable tools for tackling similar mathematical challenges. By embracing the ambiguity and fostering critical thinking, we can unlock a deeper understanding of the fascinating world of numbers and patterns. Remember that the process of discovery and the development of mathematical reasoning are equally important as the final answer itself. So, continue to explore, experiment, and enjoy the beautiful complexity of mathematics!
Latest Posts
Latest Posts
-
6 And 7 Common Denominator
Sep 13, 2025
-
Give Me Four Random Numbers
Sep 13, 2025
-
Is 2 6 Equal To 4 12
Sep 13, 2025
-
Is 1 4 Greater Than 1 2
Sep 13, 2025
-
39 3 Degrees Celsius To Fahrenheit
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 3 5 9 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.