Is 1/4 Greater Than 1/2
saludintensiva
Sep 13, 2025 · 5 min read
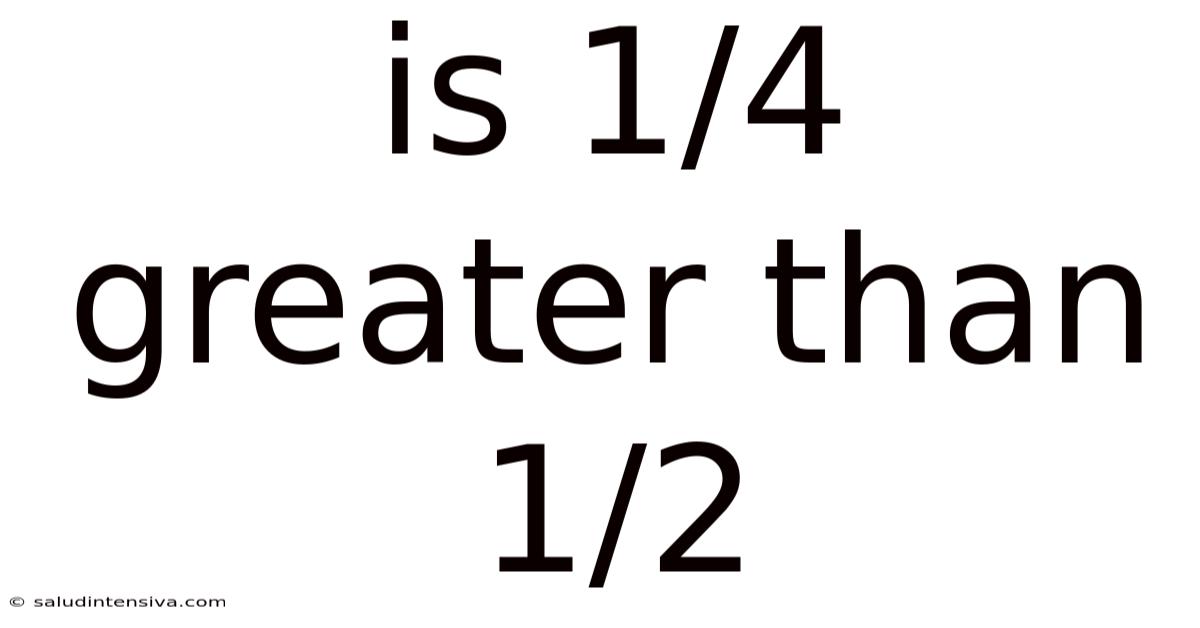
Table of Contents
Is 1/4 Greater Than 1/2? Understanding Fractions and Comparisons
Is 1/4 greater than 1/2? The answer is a resounding no. This seemingly simple question about fractions opens the door to a deeper understanding of fundamental mathematical concepts. This article will explore why 1/4 is less than 1/2, providing a comprehensive explanation suitable for various levels of understanding, from elementary school students to those looking for a refresher on fractional comparisons. We'll delve into the visual representation of fractions, their numerical representation, and practical applications to solidify this understanding.
Understanding Fractions: A Visual Approach
Fractions represent parts of a whole. The number on the top, called the numerator, indicates how many parts we have. The number on the bottom, the denominator, indicates how many equal parts the whole is divided into.
Let's visualize 1/2 and 1/4 using a simple pie chart.
Imagine a pie cut into two equal slices. 1/2 represents one of those two slices – a significant portion of the whole pie.
Now, imagine the same pie cut into four equal slices. 1/4 represents only one of these four slices. Visually, it's clear that one slice out of two is larger than one slice out of four.
This visual representation immediately demonstrates that 1/4 is smaller than 1/2.
Numerical Comparison of 1/4 and 1/2
While visual aids are helpful, we also need a numerical method to compare fractions. There are several approaches:
-
Finding a Common Denominator: This is the most common and reliable method. To compare fractions, we need to express them with the same denominator. The least common multiple (LCM) of 2 and 4 is 4.
-
We can rewrite 1/2 as 2/4 (multiply both the numerator and the denominator by 2).
-
Now we can easily compare 1/4 and 2/4. Since 1 < 2, it's clear that 1/4 < 2/4, meaning 1/4 < 1/2.
-
-
Decimal Conversion: Another approach is to convert the fractions to decimals.
- 1/2 = 0.5
- 1/4 = 0.25
Comparing 0.5 and 0.25, we see that 0.5 (1/2) is larger than 0.25 (1/4).
-
Using Number Lines: A number line can provide a visual representation of the relative sizes of fractions. Place both fractions on a number line ranging from 0 to 1. You'll see that 1/4 is closer to 0 and 1/2 is closer to 1, clearly showing that 1/2 is greater.
Real-World Examples: Understanding the Significance
Understanding the difference between 1/4 and 1/2 has practical implications in various aspects of life. Consider these examples:
-
Baking: If a recipe calls for 1/2 cup of sugar, using only 1/4 cup will significantly alter the final product's taste and texture. The dessert might be too bland or dry.
-
Measurements: In construction or engineering, precise measurements are crucial. A difference of 1/4 inch versus 1/2 inch can lead to structural issues or malfunctioning machinery.
-
Sharing: Imagine sharing a pizza. Getting 1/2 of the pizza means you receive a larger share compared to getting only 1/4.
Extending the Understanding: Comparing Other Fractions
The methods used to compare 1/4 and 1/2 can be extended to compare any two fractions. The key is to find a common denominator or convert them to decimals. Here's a step-by-step guide:
-
Find the least common denominator (LCD): This is the smallest number that is a multiple of both denominators.
-
Convert the fractions: Rewrite both fractions with the LCD as their denominator. Remember to multiply both the numerator and denominator by the same factor to maintain the fraction's value.
-
Compare the numerators: The fraction with the larger numerator is the greater fraction.
Example: Compare 2/3 and 3/4.
-
The LCD of 3 and 4 is 12.
-
Convert the fractions:
- 2/3 = (2 * 4) / (3 * 4) = 8/12
- 3/4 = (3 * 3) / (4 * 3) = 9/12
-
Compare the numerators: 8 < 9, therefore 2/3 < 3/4.
Addressing Common Misconceptions
A common misconception is that the larger the denominator, the larger the fraction. This is incorrect. The denominator tells us how many parts the whole is divided into, while the numerator tells us how many parts we have. A larger denominator means smaller pieces, not a larger portion of the whole.
Beyond Basic Comparisons: Operations with Fractions
Understanding fractional comparisons is the foundation for more advanced operations such as addition, subtraction, multiplication, and division of fractions. Mastering these basic concepts is essential for progressing in mathematics and its applications in various fields.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest way to compare fractions?
- A: Finding a common denominator is generally the simplest and most reliable method.
-
Q: Can I always use decimal conversion to compare fractions?
- A: While decimal conversion works well for many fractions, some fractions result in repeating or non-terminating decimals, making comparison less precise. The common denominator method is more universally applicable.
-
Q: Are there any online tools or calculators that can help with fraction comparison?
- A: Yes, many online calculators are readily available to assist with fraction comparisons and other fractional operations.
-
Q: How can I improve my understanding of fractions?
- A: Practice is key! Work through various examples, utilize visual aids like pie charts and number lines, and seek help when needed.
Conclusion
The question, "Is 1/4 greater than 1/2?" serves as a springboard to a comprehensive understanding of fractions and their comparisons. By using visual representations, numerical methods, and real-world examples, we've established that 1/4 is definitively smaller than 1/2. The principles and methods discussed here extend beyond this specific comparison, providing a solid foundation for tackling more complex fractional problems and solidifying a strong grasp of this essential mathematical concept. Remember, mastering fractions is crucial for success in mathematics and countless real-world applications. Consistent practice and a willingness to explore different methods will lead to confidence and proficiency in working with fractions.
Latest Posts
Latest Posts
-
7 12 In Decimal Form
Sep 13, 2025
-
3 5 As A Mixed Number
Sep 13, 2025
-
Gcf Of 10 And 35
Sep 13, 2025
-
What Is Negative 4 Squared
Sep 13, 2025
-
250 Percent As A Fraction
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.