3.5 As A Mixed Number
saludintensiva
Sep 10, 2025 · 6 min read
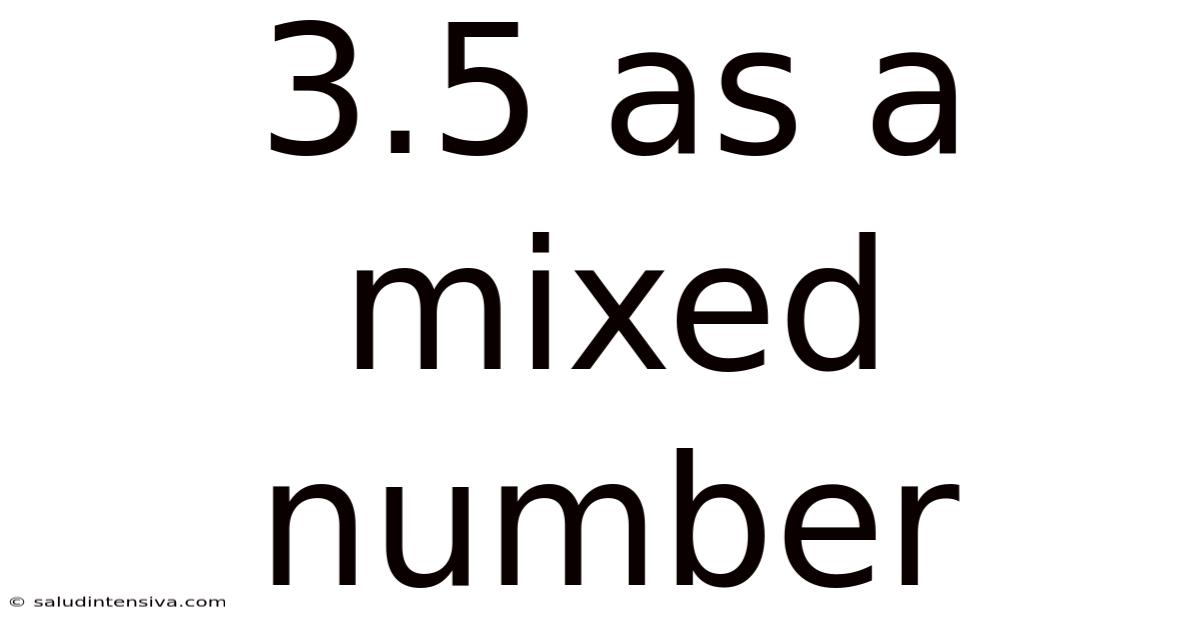
Table of Contents
Understanding 3.5 as a Mixed Number: A Comprehensive Guide
Many of us encounter decimal numbers like 3.5 in our daily lives, from calculating prices to measuring ingredients. But what does 3.5 truly represent, and how can we express it differently? This comprehensive guide will explore the concept of 3.5 as a mixed number, delving into its meaning, conversion process, practical applications, and addressing frequently asked questions. Understanding this seemingly simple concept forms a crucial foundation for more advanced mathematical operations.
What is a Mixed Number?
Before diving into the specifics of 3.5, let's define a mixed number. A mixed number is a combination of a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅓, and 5 ⅛ are all mixed numbers. They represent a quantity that's more than a whole number but less than the next whole number.
Converting Decimals to Fractions: The Foundation
The key to understanding 3.5 as a mixed number lies in converting the decimal portion (0.5) into a fraction. Remember that decimal numbers represent parts of a whole. The number to the right of the decimal point indicates the fraction. In 3.5, the ".5" represents five-tenths. We can write this as a fraction: 5/10.
Simplifying Fractions: Finding the Lowest Terms
The fraction 5/10 isn't in its simplest form. To simplify a fraction, we find the greatest common divisor (GCD) of both the numerator and denominator and divide both by that number. The GCD of 5 and 10 is 5. Dividing both the numerator and the denominator by 5 gives us:
5 ÷ 5 / 10 ÷ 5 = 1/2
Therefore, 0.5 is equivalent to ½.
Expressing 3.5 as a Mixed Number
Now that we've converted 0.5 to ½, we can express 3.5 as a mixed number. Remember that 3.5 consists of the whole number 3 and the fractional part ½. Combining these, we get:
3 ½
This is the mixed number representation of 3.5. It clearly shows that 3.5 is three and one-half.
Visual Representation: Understanding the Concept
Imagine you have three whole pizzas and half a pizza. This scenario perfectly illustrates the concept of 3.5. You have three complete units (whole numbers) and an additional half unit (fraction). This visual representation helps to solidify the understanding of the mixed number 3 ½.
Converting Mixed Numbers to Improper Fractions: An Alternate Representation
While 3 ½ is the commonly used mixed number representation, it's also useful to understand how to convert this mixed number into an improper fraction. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
To convert 3 ½ to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 3 x 2 = 6
- Add the numerator: 6 + 1 = 7
- Keep the same denominator: 2
Therefore, 3 ½ is equivalent to the improper fraction 7/2. This representation is valuable in certain mathematical operations, particularly when multiplying or dividing fractions.
Practical Applications of Understanding Mixed Numbers
Understanding mixed numbers like 3 ½ is crucial in various aspects of daily life and different fields of study:
- Cooking and Baking: Recipes often call for fractional measurements. Understanding mixed numbers allows for accurate ingredient measurement. For example, a recipe might call for 3 ½ cups of flour.
- Construction and Engineering: Precision is paramount in these fields. Measurements often involve fractions and mixed numbers to ensure accuracy in construction and design.
- Finance: Calculating interest, discounts, and profit margins often involves working with decimal numbers that can be more easily understood and manipulated as mixed numbers or fractions.
- Data Analysis and Statistics: Understanding fractions and mixed numbers is essential for interpreting data and presenting findings effectively.
Beyond 3.5: Applying the Conversion Process to Other Decimals
The process of converting decimals to mixed numbers isn't limited to 3.5. Let's explore a few more examples to solidify your understanding:
-
Converting 2.75 to a mixed number:
- The whole number is 2.
- The decimal part is 0.75, which is equivalent to ¾ (75/100 simplified).
- Therefore, 2.75 as a mixed number is 2 ¾.
-
Converting 1.6 to a mixed number:
- The whole number is 1.
- The decimal part is 0.6, which is equivalent to ⁶/₁₀, simplified to ³/₅.
- Therefore, 1.6 as a mixed number is 1 ³/₅.
-
Converting 0.875 to a mixed number:
- The whole number is 0.
- The decimal part is 0.875, which is equivalent to ⁸⁷⁵/₁₀₀₀, simplified to ⁷/₈.
- Therefore, 0.875 as a mixed number is ⁷/₈ (In this case, we don't need a whole number component because the decimal is less than 1).
Frequently Asked Questions (FAQ)
Q1: Why is it important to simplify fractions?
A1: Simplifying fractions makes them easier to understand and work with. It presents the fraction in its most concise and efficient form. For example, 5/10 is less intuitive than 1/2.
Q2: Can all decimals be converted into mixed numbers?
A2: No, only terminating decimals (decimals that end) can be directly converted into fractions and then mixed numbers. Repeating decimals (decimals that continue infinitely with a repeating pattern) require a different approach involving algebraic manipulation.
Q3: What if the decimal has more than one digit after the decimal point?
A3: The process remains the same. For example, with 12.375:
* The whole number is 12.
* The decimal 0.375 is 375/1000, which simplifies to 3/8.
* The mixed number is 12 3/8.
Q4: Is there a quicker method for converting decimals to fractions?
A4: Yes, you can place the decimal portion over a power of 10 (10, 100, 1000, etc., depending on the number of digits after the decimal point) and then simplify. For example, 0.25 becomes 25/100, which simplifies to 1/4.
Q5: How do I convert a mixed number back to a decimal?
A5: To convert a mixed number back to a decimal, divide the numerator of the fraction by the denominator and add the whole number. For example, 3 ½: 1 ÷ 2 = 0.5, then add the whole number: 3 + 0.5 = 3.5.
Conclusion: Mastering the Fundamentals
Understanding 3.5 as a mixed number—and the broader concept of converting decimals to mixed numbers—is a fundamental skill in mathematics. This knowledge isn't just about rote memorization; it's about developing a deeper understanding of numbers and their various representations. By mastering this concept, you build a solid foundation for more advanced mathematical concepts and applications across various fields. The ability to seamlessly move between decimals, fractions, and mixed numbers enhances problem-solving skills and opens doors to a more intuitive grasp of quantitative information. Continue practicing, and you'll find that working with mixed numbers becomes second nature.
Latest Posts
Latest Posts
-
What Is 3 4 In Half
Sep 10, 2025
-
Find The Height Of Cylinder
Sep 10, 2025
-
Gcf Of 14 And 18
Sep 10, 2025
-
Greatest Common Factor Of 14
Sep 10, 2025
-
1 000 Divided By 4
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3.5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.