What Is 3/4 In Half
saludintensiva
Sep 10, 2025 · 6 min read
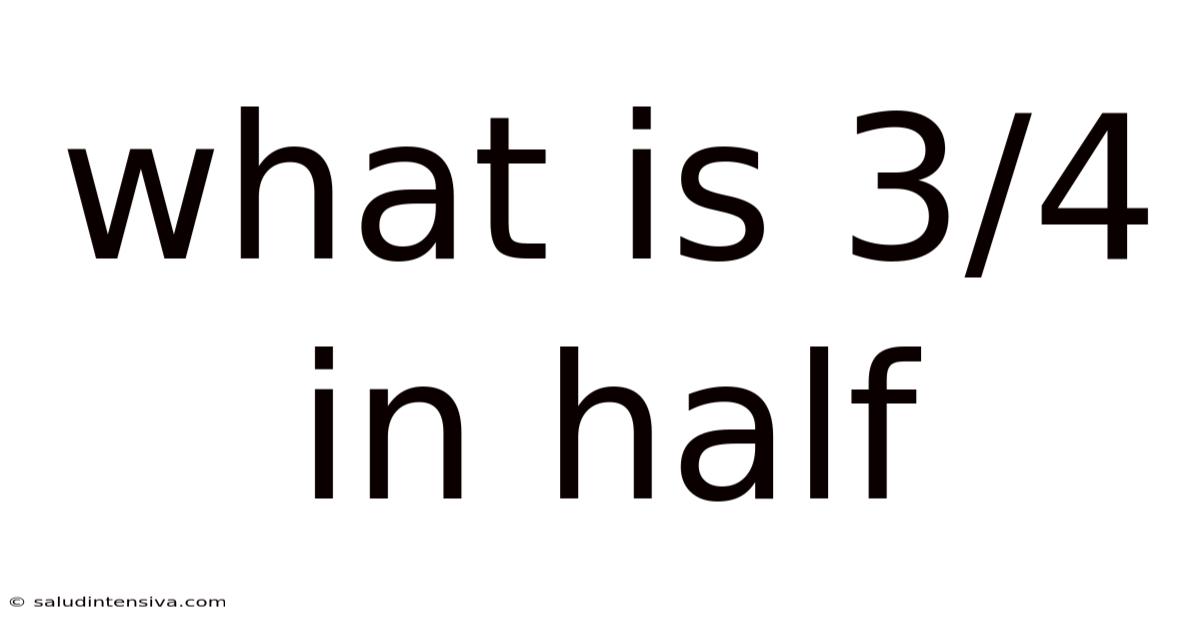
Table of Contents
What is 3/4 in Half? Understanding Fractions and Division
This article explores the concept of halving a fraction, specifically 3/4. We'll delve into the mathematical process, explain the underlying principles, and offer practical examples to solidify your understanding. This will be particularly helpful for students learning fractions, but also serves as a refresher for anyone needing a clear explanation of fraction division. Understanding this seemingly simple concept forms the bedrock of more advanced mathematical operations.
Introduction: Fractions and Their Representation
Before diving into halving 3/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator shows how many equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts of a whole.
Halving 3/4: The Mathematical Approach
Halving 3/4 means dividing it by 2. There are two common ways to approach this:
Method 1: Multiplying the Denominator
The simplest way to halve a fraction is to multiply the denominator by 2. This effectively doubles the number of parts the whole is divided into, while keeping the number of parts we have constant. So, halving 3/4 becomes:
3 / (4 * 2) = 3/8
This means that half of 3/4 is 3/8. Imagine a pizza cut into 4 slices. You have 3 slices (3/4). If you halve your share, you now have 3 slices of an 8-slice pizza (3/8).
Method 2: Converting to a Decimal and then Halving
Another approach involves converting the fraction to a decimal and then halving the decimal value.
First, convert 3/4 to a decimal:
3/4 = 0.75
Now, halve the decimal:
0.75 / 2 = 0.375
Finally, convert the decimal back into a fraction:
0.375 = 375/1000
Simplifying this fraction by dividing both the numerator and denominator by their greatest common divisor (125) gives us:
375/1000 = 3/8
This method confirms that half of 3/4 is indeed 3/8.
Visual Representation: Understanding the Concept
Visual aids can significantly help grasp the concept of halving fractions. Imagine a rectangular bar representing a whole.
- Divide the bar into 4 equal parts: Shade 3 parts to represent 3/4.
- Divide each of the 4 parts in half: You'll now have 8 equal parts.
- Observe the shaded area: You'll see that 3 of the original 4 parts are now represented by 6 of the 8 smaller parts. This visually demonstrates that half of 3/4 is 3/8.
This visual approach makes the abstract concept of fraction division more concrete and easily understandable.
Further Exploration: Halving Other Fractions
The principles discussed above apply to halving any fraction. To halve a fraction a/b, you can either:
- Multiply the denominator by 2: This results in the fraction a/(2b).
- Convert to a decimal, halve, and then convert back to a fraction: This involves dividing a by b, dividing the resulting decimal by 2, and converting the new decimal back into a fraction.
For instance, let's halve 2/5:
Method 1: 2 / (5 * 2) = 2/10 = 1/5
Method 2: 2/5 = 0.4; 0.4 / 2 = 0.2; 0.2 = 2/10 = 1/5
Both methods yield the same result: half of 2/5 is 1/5.
Practical Applications: Real-World Examples
Understanding how to halve fractions isn't just an abstract mathematical exercise; it has practical applications in many real-world scenarios.
- Cooking: A recipe calls for 3/4 cup of flour, but you want to halve the recipe. You need to calculate half of 3/4 cup, which is 3/8 cup.
- Sewing: You need to cut a piece of fabric that is 3/4 of a yard long, but only need half that length. Calculating half of 3/4 of a yard will give you the precise measurement.
- Construction: In construction projects, precise measurements are critical. Halving fractional measurements is often necessary for accurate calculations.
- Sharing Resources: If you have 3/4 of a pizza and want to share it equally with a friend, you'll need to find half of 3/4 to determine each person's share.
These examples highlight the relevance of understanding fraction division in everyday life.
Explanation of the Underlying Mathematical Principles
The process of halving a fraction is fundamentally a division operation. When we divide a fraction by 2, we are essentially multiplying the fraction by its reciprocal (1/2).
Remember that dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a number is simply 1 divided by that number. Therefore, dividing by 2 is the same as multiplying by 1/2.
So, halving 3/4 can be expressed as:
(3/4) / 2 = (3/4) * (1/2) = (3 * 1) / (4 * 2) = 3/8
This demonstrates the mathematical equivalence of dividing a fraction by 2 and multiplying it by 1/2.
Frequently Asked Questions (FAQ)
-
Q: Can I halve a fraction by halving the numerator? A: No, halving only the numerator would change the value of the fraction. You need to either multiply the denominator by 2 or use the method of converting to a decimal and then halving.
-
Q: What if I need to divide a fraction by a number other than 2? A: The principle remains the same. To divide a fraction by any number 'x', multiply the fraction by its reciprocal (1/x).
-
Q: Are there other methods to halve a fraction? A: While the two primary methods (multiplying the denominator by 2 and converting to a decimal) are the most straightforward, you could also represent the fraction visually using diagrams or manipulate the fraction algebraically.
Conclusion: Mastering Fractions: A Building Block for Success
Mastering the concept of halving fractions is a crucial step in developing a strong foundation in mathematics. This seemingly simple skill underpins more complex mathematical operations and has numerous practical applications in various aspects of life. By understanding both the mathematical process and the underlying principles, you can confidently tackle fraction division and apply this knowledge to solve real-world problems. Remember to practice regularly using different methods to solidify your understanding. With consistent effort, you'll gain proficiency in handling fractions and enhance your overall mathematical abilities. The ability to effortlessly manipulate fractions will not only improve your scores in math classes but also equip you with valuable problem-solving skills applicable across many disciplines.
Latest Posts
Latest Posts
-
84 Degrees Fahrenheit To Celsius
Sep 10, 2025
-
31 Acres To Sq Ft
Sep 10, 2025
-
1 15 As A Decimal
Sep 10, 2025
-
1 89 Meters To Feet
Sep 10, 2025
-
1 12th As A Decimal
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 In Half . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.