2 3 Divided By 4
saludintensiva
Sep 14, 2025 · 6 min read
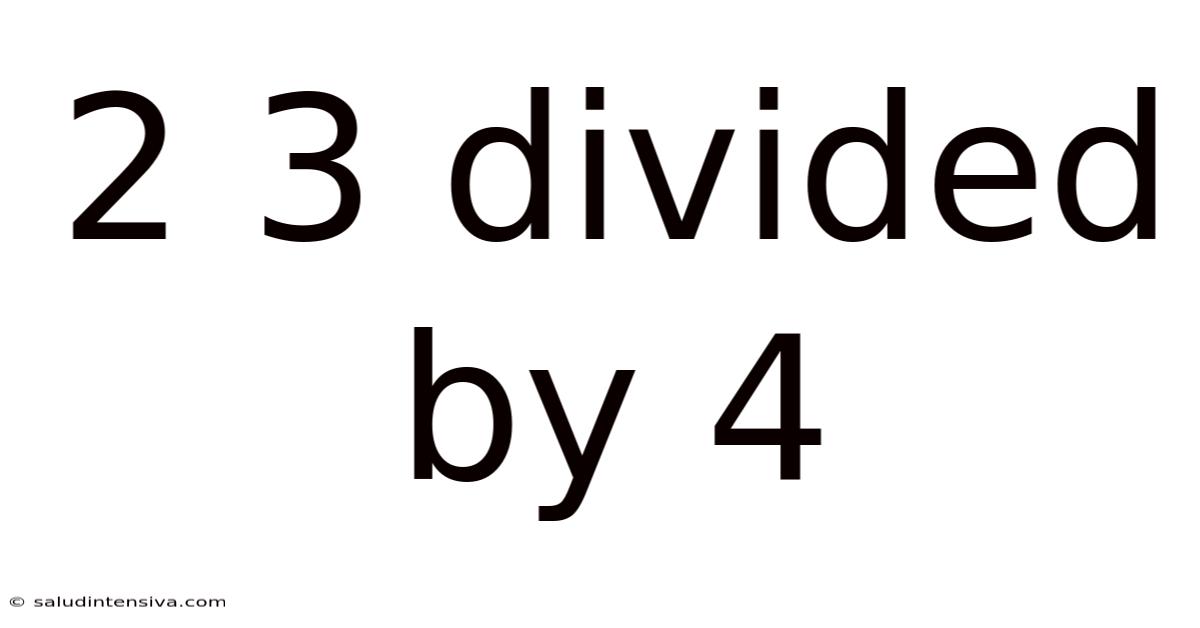
Table of Contents
Decoding 2/3 Divided by 4: A Comprehensive Guide
Understanding fractions and division can be challenging, especially when combining the two. This article provides a comprehensive guide to solving the equation 2/3 divided by 4, explaining the process step-by-step and exploring the underlying mathematical concepts. We'll cover various methods, addressing potential misconceptions and solidifying your understanding of fraction division. This will be particularly useful for students learning about fractions and division, as well as anyone looking to refresh their understanding of basic arithmetic.
Understanding Fractions and Division
Before diving into the solution, let's refresh our understanding of fractions and division. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many parts make up the whole.
Division, on the other hand, is the process of splitting a quantity into equal parts. When dividing by a whole number, we're essentially splitting the quantity into that many equal groups. Dividing fractions introduces a slight twist, as we're dealing with parts of wholes.
Method 1: Reciprocate and Multiply
The most common and arguably easiest method for dividing fractions is to reciprocate the divisor and multiply. This means we flip the second fraction (the divisor) upside down and then multiply the two fractions.
Steps:
-
Rewrite the problem: 2/3 ÷ 4 can be rewritten as (2/3) ÷ (4/1). Remember that any whole number can be expressed as a fraction with a denominator of 1.
-
Reciprocate the divisor: The divisor is 4/1. Reciprocating it gives us 1/4.
-
Multiply the fractions: Now, we multiply the first fraction (2/3) by the reciprocal of the second fraction (1/4): (2/3) x (1/4).
-
Multiply the numerators and denominators: Multiply the numerators together (2 x 1 = 2) and the denominators together (3 x 4 = 12). This gives us the fraction 2/12.
-
Simplify the fraction: Finally, we simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 2 and 12 is 2. Dividing both the numerator and denominator by 2, we get the simplified fraction 1/6.
Therefore, 2/3 divided by 4 is equal to 1/6.
Method 2: Visual Representation
Visualizing the problem can be incredibly helpful, especially for beginners. Imagine you have a pizza cut into 3 equal slices. You have 2 of those slices (2/3 of the pizza). Now, you want to divide those 2 slices equally among 4 people.
To do this, you would first divide each of your 2 slices into 4 equal parts. This results in a total of 8 smaller slices (2 slices x 4 parts/slice = 8 parts). Each person would then receive 2 of these smaller slices (8 parts / 4 people = 2 parts/person).
Since the original pizza was cut into 3 slices, and we've now divided each of those slices into 4, the pizza is now effectively cut into 12 smaller slices (3 slices x 4 parts/slice = 12 parts). Each person receives 2 out of those 12 slices, representing 2/12 of the original pizza. Simplifying this fraction, we again arrive at 1/6.
Method 3: Converting to Decimal Numbers (Alternative Approach)
While not strictly necessary, converting the fraction to a decimal can offer an alternative perspective.
-
Convert the fraction to a decimal: 2/3 is approximately 0.6667 (repeating decimal).
-
Divide the decimal by the whole number: 0.6667 ÷ 4 ≈ 0.1667
-
Convert back to a fraction (optional): Converting 0.1667 back to a fraction is more challenging and may not always result in a precise answer due to rounding errors. However, if we recognize that 0.1667 is approximately 1/6, we reach the same conclusion.
Explanation with Scientific Notation
While not typically used for this level of arithmetic, understanding scientific notation can provide a different perspective on the magnitude of the operation. Though less practical for this specific problem, it's beneficial for understanding the broader concept of fraction division in a more formal way. We could represent 2/3 as approximately 6.67 x 10<sup>-1</sup> and 4 as 4 x 10<sup>0</sup>. Division would involve subtracting the exponents and dividing the coefficients, although this is not a straightforward or efficient method for this particular equation. It's more suited for significantly larger or smaller numbers.
Frequently Asked Questions (FAQ)
Q: Why do we reciprocate and multiply when dividing fractions?
A: Reciprocating and multiplying is a shortcut that stems from the definition of division. Dividing by a fraction is the same as multiplying by its reciprocal. This is because division is the inverse operation of multiplication.
Q: Can I divide the numerators and denominators directly when dividing fractions?
A: No. You can only directly divide numerators and denominators when multiplying fractions. When dividing fractions, you must reciprocate the second fraction before multiplying.
Q: What if the divisor is a decimal instead of a whole number?
A: Convert the decimal to a fraction first, then follow the steps outlined above. For example, if you were dividing 2/3 by 0.5 (which is 1/2), you would reciprocate 1/2 to get 2/1 and multiply (2/3) x (2/1) = 4/3.
Q: What if I get a large fraction after simplifying?
A: Large fractions are perfectly acceptable. Sometimes, a large fraction is the most accurate representation of the answer. You can, however, convert it into a mixed number (a whole number and a fraction) if desired. For example, 4/3 can be expressed as 1 1/3.
Q: Are there other ways to solve this problem?
A: Yes, although the reciprocate and multiply method is the most efficient. You could also use visual aids, decimal conversion (as shown above), or long division, though the latter can be cumbersome with fractions.
Conclusion
Dividing 2/3 by 4 results in 1/6. We've explored three different methods to solve this problem: reciprocating and multiplying, visual representation, and decimal conversion. Understanding these methods not only helps solve this specific problem but also builds a solid foundation for tackling more complex fraction division problems in the future. Remember the key is to master the concept of reciprocation and the logic behind why this method works. The ability to understand and visualize the division process will be invaluable as you progress in your mathematical journey. Don't hesitate to practice using these methods with different fractions to solidify your understanding!
Latest Posts
Latest Posts
-
10 8 In Simplest Form
Sep 15, 2025
-
Gcf Of 4 And 16
Sep 15, 2025
-
6 11 As A Percentage
Sep 15, 2025
-
Whats Equivalent To 4 5
Sep 15, 2025
-
Square Root Of 4 9
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.