6 11 As A Percentage
saludintensiva
Sep 15, 2025 · 5 min read
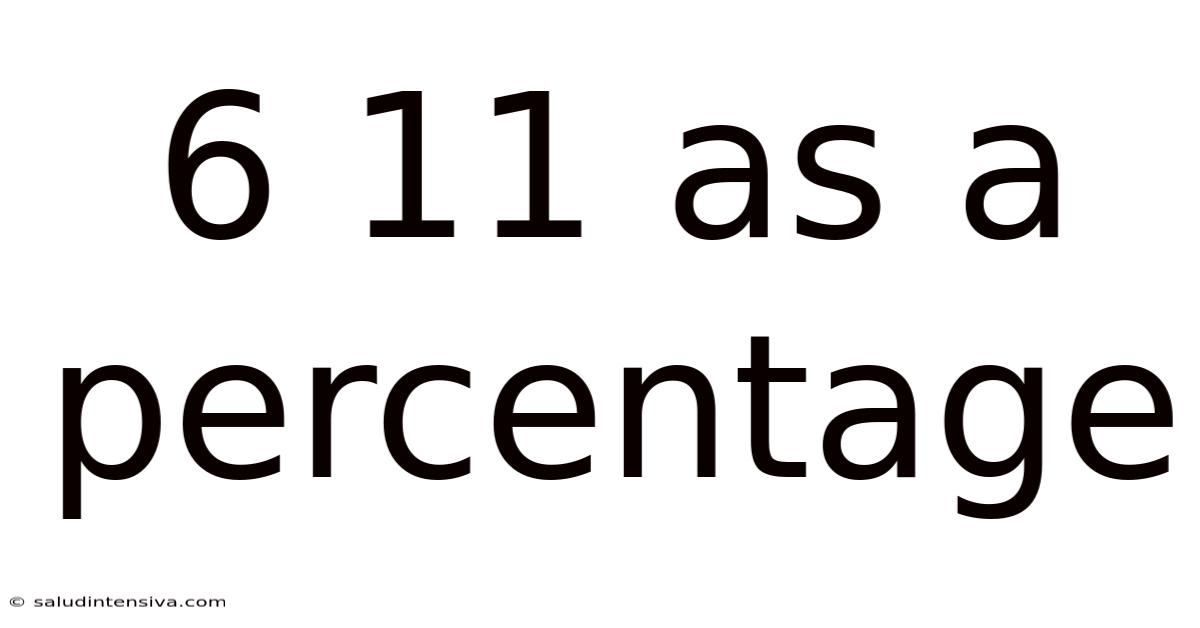
Table of Contents
6/11 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications across numerous fields, from finance and statistics to everyday life. This comprehensive guide will explore the conversion of the fraction 6/11 into a percentage, delving into the process, explaining the underlying principles, and providing practical examples. We'll also address common misconceptions and frequently asked questions. Mastering this concept will significantly enhance your numerical literacy and problem-solving capabilities.
Understanding Fractions and Percentages
Before diving into the specifics of converting 6/11, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates the total number of parts in the whole.
A percentage, on the other hand, is a way of expressing a fraction or a ratio as a number out of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." Percentages are widely used because they provide a standardized way to compare different proportions.
Converting 6/11 to a Percentage: The Step-by-Step Process
The conversion of a fraction to a percentage involves two primary steps:
-
Converting the Fraction to a Decimal: To convert a fraction to a decimal, we divide the numerator by the denominator. In our case:
6 ÷ 11 ≈ 0.54545454...
Notice that this is a recurring decimal, meaning the digits 54 repeat infinitely. We'll address how to handle this shortly.
-
Converting the Decimal to a Percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.54545454... × 100 ≈ 54.545454...%
Handling Recurring Decimals
As we've seen, 6/11 results in a recurring decimal. For practical purposes, we usually round the decimal to a certain number of decimal places. The level of precision required depends on the context. For example:
- Rounded to one decimal place: 54.5%
- Rounded to two decimal places: 54.55%
- Rounded to three decimal places: 54.545%
The more decimal places you use, the more accurate your percentage will be, but it may also be less convenient to work with. Choosing the appropriate level of precision is crucial for accurate representation without unnecessary complexity.
Alternative Method: Using Proportions
Another approach to converting 6/11 to a percentage involves setting up a proportion. We know that a percentage is a fraction out of 100. Therefore, we can set up the following proportion:
6/11 = x/100
To solve for x (the percentage), we can cross-multiply:
11x = 600
x = 600/11 ≈ 54.545454...
This confirms our previous result.
Practical Applications and Real-World Examples
The ability to convert fractions to percentages is incredibly useful in various situations:
-
Calculating Grades: If you scored 6 out of 11 questions correctly on a test, your score is approximately 54.55%.
-
Financial Calculations: Understanding percentages is crucial for calculating interest rates, discounts, profit margins, and taxes. For instance, if 6 out of 11 investments are profitable, the success rate is approximately 54.55%.
-
Data Analysis: Percentages are extensively used to represent data in charts, graphs, and reports. For example, if a survey shows 6 out of 11 respondents prefer a particular product, the percentage preference is around 54.55%.
-
Everyday Life: Percentages are used in various everyday contexts, such as calculating tips, discounts, or understanding sales tax.
Common Misconceptions
A common mistake is confusing the fraction with the percentage. Remember that 6/11 is a fraction, while approximately 54.55% is its equivalent representation as a percentage. These are two different but equivalent ways of expressing the same proportion.
Further Exploration: Working with Different Fractions
The method outlined above can be applied to convert any fraction to a percentage. For example:
- 1/4: 1 ÷ 4 = 0.25; 0.25 × 100 = 25%
- 3/5: 3 ÷ 5 = 0.6; 0.6 × 100 = 60%
- 7/8: 7 ÷ 8 = 0.875; 0.875 × 100 = 87.5%
Practice converting different fractions will reinforce your understanding and improve your proficiency.
Frequently Asked Questions (FAQs)
-
Q: Why do we multiply by 100 when converting a decimal to a percentage?
- A: A percentage represents a fraction out of 100. Multiplying by 100 scales the decimal to express it as a value out of 100.
-
Q: How many decimal places should I round to?
- A: The number of decimal places depends on the required level of accuracy. In most everyday situations, rounding to one or two decimal places is sufficient. However, in scientific or financial contexts, higher precision might be needed.
-
Q: Can I convert a percentage back to a fraction?
- A: Yes, to convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 54.55% is equivalent to 54.55/100, which can be simplified to 1091/2000.
-
Q: What if the fraction is an improper fraction (numerator is larger than the denominator)?
- A: The process remains the same. Divide the numerator by the denominator to obtain the decimal, then multiply by 100 to get the percentage. The resulting percentage will be greater than 100%.
-
Q: What if the denominator is zero?
- A: Division by zero is undefined in mathematics. A fraction with a denominator of zero is not a valid mathematical expression.
Conclusion
Converting 6/11 to a percentage, approximately 54.55%, involves a straightforward process of dividing the numerator by the denominator and then multiplying the result by 100. Understanding this process is crucial for various applications across different disciplines. Remember to choose an appropriate level of precision when rounding recurring decimals. With practice and a clear grasp of the underlying principles, you'll confidently convert fractions to percentages and apply this fundamental skill to solve a wide range of problems. Mastering this concept significantly enhances your mathematical abilities and provides you with a valuable tool for navigating various numerical challenges in your personal and professional life.
Latest Posts
Latest Posts
-
Gcf For 16 And 20
Sep 15, 2025
-
Midway Point Between Two Locations
Sep 15, 2025
-
What Percent Is 7 8
Sep 15, 2025
-
V 2 V0 2 2ax
Sep 15, 2025
-
6 And 9 Common Multiples
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 6 11 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.