V 2 V0 2 2ax
saludintensiva
Sep 15, 2025 · 6 min read
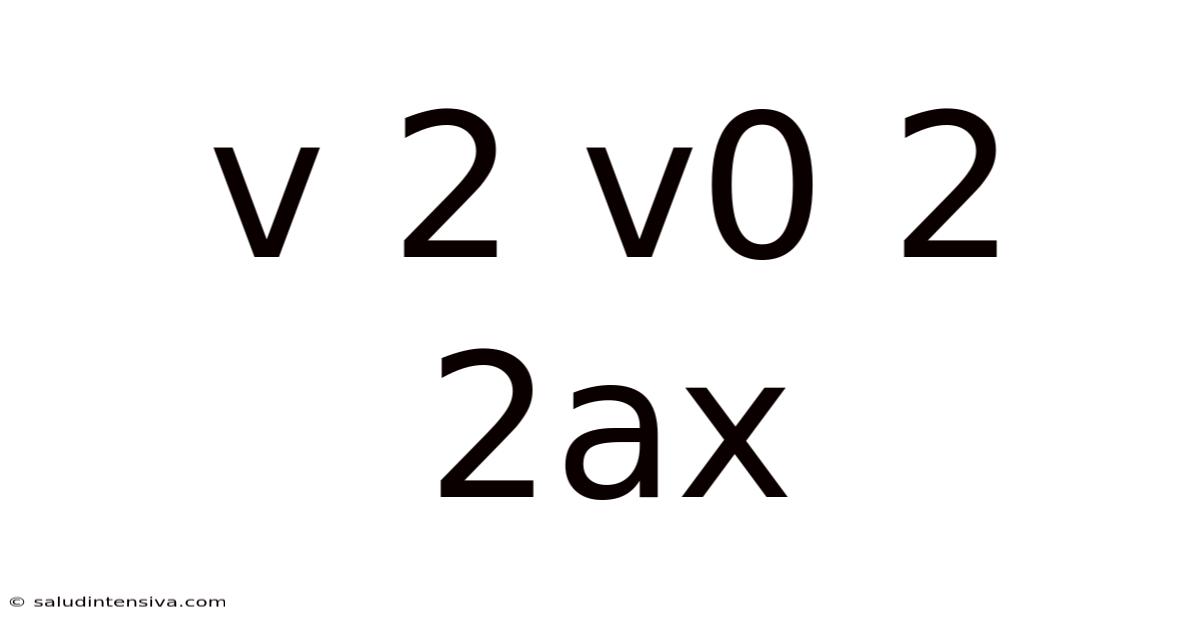
Table of Contents
Unveiling the Secrets of v² = v₀² + 2ax: A Comprehensive Guide to Understanding Constant Acceleration
This article delves into the crucial kinematic equation, v² = v₀² + 2ax, explaining its derivation, applications, and significance in understanding motion under constant acceleration. We'll explore how this equation helps us analyze various real-world scenarios, from analyzing the motion of a falling object to understanding the performance of vehicles. This exploration will include detailed explanations, worked examples, and frequently asked questions to solidify your understanding.
Introduction: Understanding the Fundamentals of Motion
Understanding motion is fundamental to physics. When an object's velocity changes over time, it experiences acceleration. If this acceleration remains constant, we can use a set of simplified equations, known as kinematic equations, to describe its motion. One of the most useful of these equations is v² = v₀² + 2ax. This equation relates the final velocity (v) of an object to its initial velocity (v₀), acceleration (a), and displacement (x). This equation is incredibly powerful because it doesn't require knowing the time elapsed. This makes it particularly useful in scenarios where time isn't readily measurable or isn't the primary focus of the analysis.
Deriving the Equation: A Journey from First Principles
Let's derive this vital equation from first principles, starting with the fundamental definitions of velocity and acceleration.
-
Velocity (v): The rate of change of displacement (x) with respect to time (t). Mathematically, this is represented as v = dx/dt.
-
Acceleration (a): The rate of change of velocity (v) with respect to time (t). Mathematically, this is represented as a = dv/dt.
For constant acceleration, we can use the following equations:
-
v = v₀ + at: This equation tells us that the final velocity (v) is equal to the initial velocity (v₀) plus the product of acceleration (a) and time (t).
-
x = v₀t + ½at²: This equation calculates the displacement (x) based on initial velocity, acceleration, and time.
To derive v² = v₀² + 2ax, we can employ a clever substitution. Let's solve equation (1) for time (t):
t = (v - v₀) / a
Now, substitute this expression for 't' into equation (2):
x = v₀[(v - v₀)/a] + ½a[(v - v₀)/a]²
Simplifying this equation, we get:
x = [v₀v - v₀²]/a + ½a[v² - 2vv₀ + v₀²]/a²
Further simplification leads us to:
ax = v₀v - v₀² + ½v² - vv₀ + ½v₀²
Rearranging the terms to isolate v², we arrive at our desired equation:
v² = v₀² + 2ax
Applications: Real-World Scenarios and Problem Solving
This equation finds extensive applications across various fields:
-
Projectile Motion: Analyzing the vertical motion of projectiles, neglecting air resistance, allows us to determine the final velocity of a projectile at a given height. For instance, determining the impact velocity of a ball dropped from a certain height.
-
Vehicle Dynamics: Calculating the braking distance of a car, given its initial speed and deceleration, is a crucial application. It helps determine safe stopping distances and design efficient braking systems.
-
Free Fall: This equation accurately describes the motion of objects in free fall under the influence of gravity. Calculating the final velocity of an object just before it hits the ground is a straightforward application.
-
Linear Motion with Constant Acceleration: Any scenario involving linear motion (motion in a straight line) with constant acceleration can be analyzed using this equation. Examples include the acceleration of a train or the deceleration of a roller coaster.
Worked Examples: Putting the Equation into Practice
Let's illustrate the application of v² = v₀² + 2ax with a few examples:
Example 1: Stopping a Car
A car traveling at 20 m/s brakes with a constant deceleration of 5 m/s². How far does the car travel before coming to a complete stop?
Here, v₀ = 20 m/s, v = 0 m/s (car comes to a stop), and a = -5 m/s² (negative because it's deceleration). We need to find x.
0² = 20² + 2(-5)x
Solving for x, we get:
x = 40 meters
Therefore, the car travels 40 meters before stopping.
Example 2: Falling Object
An object is dropped from a height of 100 meters. Ignoring air resistance and using g ≈ 9.8 m/s² (acceleration due to gravity), what is its velocity just before it hits the ground?
Here, v₀ = 0 m/s (dropped, not thrown), a = 9.8 m/s², and x = 100 m. We need to find v.
v² = 0² + 2(9.8)(100)
v = √(1960) ≈ 44.3 m/s
The object's velocity just before hitting the ground is approximately 44.3 m/s.
Limitations: When the Equation Doesn't Apply
It is crucial to understand the limitations of v² = v₀² + 2ax:
-
Constant Acceleration: This equation only applies when the acceleration is constant. If the acceleration changes during the motion, this equation will not give accurate results.
-
Linear Motion: The equation only applies to linear motion; it cannot be directly applied to situations involving rotational motion or curvilinear motion.
-
Neglecting Other Forces: In many real-world scenarios, factors like air resistance or friction are significant. This equation often simplifies the problem by neglecting these forces. While sometimes a reasonable approximation, this should be considered when interpreting results.
Frequently Asked Questions (FAQ)
Q1: What happens if the acceleration is zero?
If the acceleration (a) is zero, the equation simplifies to v² = v₀², implying that the final velocity is equal to the initial velocity. This makes sense; if there is no acceleration, the velocity remains constant.
Q2: Can this equation be used for upward motion against gravity?
Yes, but remember to use a negative value for acceleration (a) since gravity acts downwards, opposing upward motion.
Q3: How is this equation related to other kinematic equations?
This equation is interconnected with other kinematic equations. It's derived from them and can be used in conjunction with them to solve more complex motion problems.
Q4: What are the units used in this equation?
The units must be consistent throughout. Commonly used units are meters (m) for displacement (x), meters per second (m/s) for velocity (v and v₀), and meters per second squared (m/s²) for acceleration (a).
Conclusion: Mastering a Fundamental Tool in Physics
The equation v² = v₀² + 2ax is a powerful tool for analyzing motion under constant acceleration. Understanding its derivation, applications, and limitations allows for a deeper grasp of kinematics and its role in solving a wide range of problems. By mastering this equation and its implications, you gain a valuable skill in comprehending and quantifying the physical world around us. Remember to always consider the assumptions and limitations of the equation to ensure its appropriate application in specific scenarios. This equation serves as a fundamental building block for more advanced concepts in physics, underscoring its importance in developing a strong foundation in the subject. Practice using it in various contexts to further refine your understanding and problem-solving abilities.
Latest Posts
Latest Posts
-
3 5 In Decimal Form
Sep 15, 2025
-
42 9 As A Decimal
Sep 15, 2025
-
13 6 As A Decimal
Sep 15, 2025
-
Is 4 8 Greater Than 1 2
Sep 15, 2025
-
Perimeter Of A Square Acre
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about V 2 V0 2 2ax . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.