Is 4/8 Greater Than 1/2
saludintensiva
Sep 15, 2025 · 6 min read
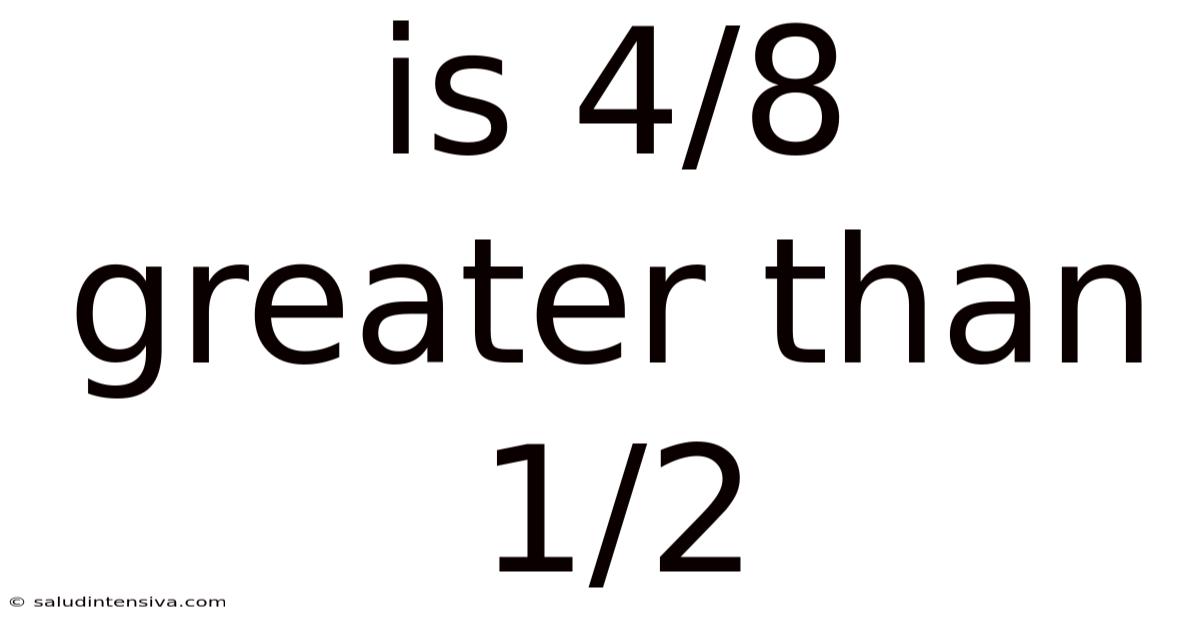
Table of Contents
Is 4/8 Greater Than 1/2? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to understanding complex financial concepts. A common question that often arises, especially for beginners, is whether one fraction is greater than another. This article will delve into the question: is 4/8 greater than 1/2? We'll explore the methods for comparing fractions, provide a clear answer, and expand your understanding of fraction equivalence and simplification.
Introduction to Fractions
Before we tackle the main question, let's briefly review the basics of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the denominator 4 means the whole is divided into four equal parts, and the numerator 3 means we're considering three of those parts.
Comparing Fractions: Different Approaches
There are several ways to compare fractions and determine which is larger. The most common methods include:
-
Finding a Common Denominator: This involves converting the fractions so they share the same denominator. Once they have the same denominator, you can simply compare the numerators. The fraction with the larger numerator is the larger fraction.
-
Converting to Decimals: You can convert each fraction to its decimal equivalent by dividing the numerator by the denominator. Then, you can directly compare the decimal values.
-
Visual Representation: Using diagrams or models (like circles or rectangles divided into equal parts) can provide a visual understanding of the relative sizes of the fractions. This is particularly helpful for beginners.
Is 4/8 Greater Than 1/2? The Solution
Now, let's address the central question: Is 4/8 greater than 1/2?
We can use any of the methods mentioned above to compare these fractions. Let's explore each:
1. Finding a Common Denominator:
The denominators of 4/8 and 1/2 are 8 and 2, respectively. The least common multiple (LCM) of 8 and 2 is 8. Therefore, we need to convert 1/2 to an equivalent fraction with a denominator of 8.
To do this, we multiply both the numerator and the denominator of 1/2 by 4:
(1 * 4) / (2 * 4) = 4/8
Now we can compare 4/8 and 4/8. Since their numerators and denominators are identical, they are equal. Therefore, 4/8 is not greater than 1/2; it is equal to 1/2.
2. Converting to Decimals:
To convert 4/8 to a decimal, we divide 4 by 8:
4 ÷ 8 = 0.5
To convert 1/2 to a decimal, we divide 1 by 2:
1 ÷ 2 = 0.5
Both fractions are equal to 0.5. Therefore, 4/8 is not greater than 1/2; they are equal.
3. Visual Representation:
Imagine a pizza cut into 8 equal slices. 4/8 represents 4 out of those 8 slices. Now, imagine another pizza cut into 2 equal halves. 1/2 represents 1 of those 2 halves. If you compare the amount of pizza represented by 4/8 and 1/2, you'll see they represent the same amount. Therefore, 4/8 is not greater than 1/2; they are equal.
Simplifying Fractions
The fraction 4/8 can be simplified. Both the numerator (4) and the denominator (8) are divisible by 4. Dividing both by 4 gives us:
4 ÷ 4 / 8 ÷ 4 = 1/2
This demonstrates that 4/8 and 1/2 are equivalent fractions; they represent the same value. Simplifying fractions is a crucial step in making them easier to understand and compare. It also helps in performing calculations more efficiently.
Understanding Equivalent Fractions
Equivalent fractions are fractions that represent the same value, even though they have different numerators and denominators. They are essentially different ways of expressing the same portion of a whole. For example, 1/2, 2/4, 3/6, 4/8, and so on, are all equivalent fractions. They all represent one-half of a whole.
Beyond the Basics: Working with More Complex Fractions
The principles discussed here – finding a common denominator, converting to decimals, and simplifying fractions – are fundamental for working with more complex fraction problems. These methods will allow you to compare any two fractions, regardless of their numerators and denominators.
For instance, to compare 5/6 and 7/8, you could find a common denominator (24), converting them to 20/24 and 21/24 respectively, revealing that 7/8 is greater than 5/6. Alternatively, converting them to decimals (approximately 0.833 and 0.875) leads to the same conclusion.
Frequently Asked Questions (FAQ)
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to work with and understand. A simplified fraction represents the same value in a more concise form, reducing the complexity of calculations and comparisons.
-
Q: How do I find the least common multiple (LCM)?
- A: The LCM is the smallest number that is a multiple of both (or all) numbers involved. One method is to list the multiples of each number until you find the smallest common multiple. Alternatively, you can use prime factorization to find the LCM more efficiently.
-
Q: Can I always convert fractions to decimals for comparison?
- A: Yes, you can always convert fractions to decimals for comparison. However, sometimes the decimal representation might be a non-terminating or repeating decimal, making it slightly less precise for comparison in some cases. The common denominator method generally provides a more precise comparison.
-
Q: What if the fractions are negative?
- A: The same principles apply to comparing negative fractions. However, remember that the larger the absolute value of a negative fraction, the smaller the fraction is. For instance, -1/2 is greater than -3/4.
Conclusion: 4/8 is Equal to 1/2, Not Greater Than
In conclusion, 4/8 is not greater than 1/2; it is equal to 1/2. This is because both fractions represent the same proportion of a whole. We've explored various methods for comparing fractions and emphasized the importance of simplifying fractions and understanding equivalent fractions. Mastering these concepts is essential for progressing in mathematics and applying these skills to various real-world scenarios. This understanding lays the groundwork for more advanced mathematical concepts involving fractions, ratios, and proportions. Remember to practice regularly, and don't hesitate to revisit the different methods explained in this article as you tackle increasingly complex fraction problems. With consistent practice, you'll become confident and proficient in comparing and working with fractions.
Latest Posts
Latest Posts
-
What Is 1 4 Percentage
Sep 15, 2025
-
Calculate Variance Of A Portfolio
Sep 15, 2025
-
Fractions Equivalent To 3 10
Sep 15, 2025
-
12 Weeks From May 1st
Sep 15, 2025
-
What Is 3 Times 1 5
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Is 4/8 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.