2/3 Is Equivalent To What
saludintensiva
Sep 16, 2025 · 6 min read
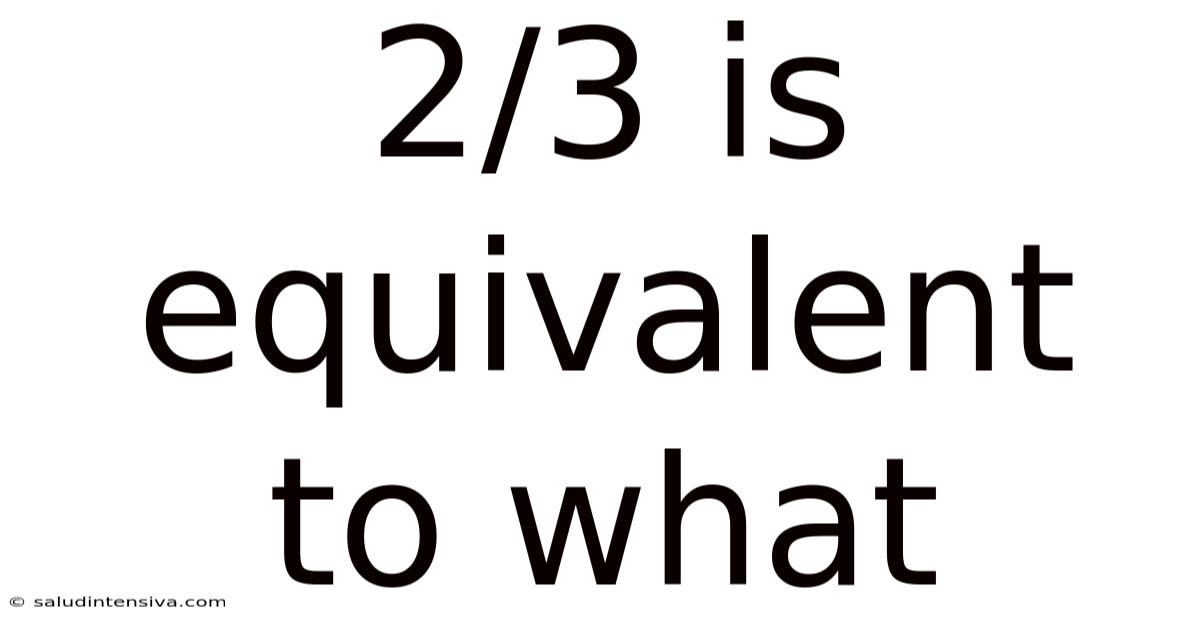
Table of Contents
2/3 is Equivalent to What? A Comprehensive Exploration of Fractions and Equivalents
Understanding fractions is fundamental to mathematics and everyday life. From baking a cake to calculating discounts, the ability to manipulate and understand fractions is invaluable. This article delves deep into the concept of fractional equivalence, focusing specifically on the fraction 2/3 and its numerous equivalent forms. We'll explore different methods for finding equivalents, the underlying mathematical principles, and practical applications, ensuring a thorough understanding for learners of all levels.
Introduction: The World of Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, 2/3 means the whole is divided into three equal parts, and we're considering two of those parts.
The fraction 2/3 is a common fraction, and understanding its equivalents is crucial. Equivalent fractions represent the same proportion or value, even though they look different. This means that 2/3 is equal to several other fractions, all representing the same portion of a whole. This article will guide you through the process of finding these equivalent fractions and understanding the underlying mathematical concepts.
Methods for Finding Equivalent Fractions of 2/3
Several methods can be used to find equivalent fractions for 2/3. The core principle behind all these methods is the concept of multiplying or dividing both the numerator and the denominator by the same non-zero number. This maintains the ratio and, therefore, the value of the fraction.
1. Multiplying the Numerator and Denominator:
The simplest method is to multiply both the numerator and the denominator by the same whole number. Let's illustrate this:
- Multiply by 2: (2 x 2) / (3 x 2) = 4/6
- Multiply by 3: (2 x 3) / (3 x 3) = 6/9
- Multiply by 4: (2 x 4) / (3 x 4) = 8/12
- Multiply by 5: (2 x 5) / (3 x 5) = 10/15
- Multiply by 10: (2 x 10) / (3 x 10) = 20/30
And so on. We can generate an infinite number of equivalent fractions for 2/3 by multiplying both the numerator and the denominator by any whole number greater than 1.
2. Dividing the Numerator and Denominator (Simplification):
While the previous method generates larger equivalent fractions, we can also find smaller equivalent fractions by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
In the case of 2/3, the GCD of 2 and 3 is 1. This means that 2/3 is already in its simplest form; we cannot divide both the numerator and the denominator by any whole number greater than 1 to obtain a simpler fraction.
3. Using Decimal Representation:
Another way to understand equivalent fractions is to consider their decimal representation. To find the decimal equivalent of 2/3, we perform the division: 2 ÷ 3 = 0.6666... (a repeating decimal). Any fraction that results in the same decimal value (0.6666...) will be equivalent to 2/3.
Understanding the Mathematical Principles
The process of finding equivalent fractions relies on the fundamental property of fractions: Multiplying or dividing both the numerator and the denominator by the same non-zero number does not change the value of the fraction. This is because a fraction represents a ratio, and multiplying or dividing both parts of a ratio by the same number maintains the proportional relationship.
Consider the fraction 2/3 as representing two parts out of three equal parts. If we multiply both the numerator and denominator by 2, we get 4/6. This represents four parts out of six equal parts, but the proportion remains the same – it's still two-thirds of the whole. Similarly, dividing both parts by a common divisor (if one exists) simplifies the representation without changing the inherent value.
Practical Applications of Equivalent Fractions
Equivalent fractions have numerous practical applications in various fields:
-
Cooking and Baking: Recipes often use fractions. Understanding equivalent fractions allows for scaling recipes up or down. For instance, if a recipe calls for 2/3 cup of flour, you could easily substitute 4/6 cup or 6/9 cup without altering the result.
-
Construction and Engineering: Precise measurements are crucial in construction. Equivalent fractions help in converting measurements to different units or simplifying calculations.
-
Finance: Calculating percentages, discounts, and interest often involves working with fractions. Understanding equivalents ensures accurate calculations.
-
Data Analysis: Representing data as fractions and using equivalent forms can aid in comparing and interpreting data sets more effectively.
Illustrative Examples: Real-World Scenarios
Let's look at some examples to illustrate the practical use of equivalent fractions of 2/3:
Example 1: Sharing Pizza
You have a pizza cut into 9 slices. If you want to eat 2/3 of the pizza, how many slices should you eat?
Since 2/3 is equivalent to 6/9 (multiply numerator and denominator by 3), you should eat 6 slices.
Example 2: Scaling a Recipe
A recipe calls for 2/3 cup of sugar. You want to double the recipe. How much sugar do you need?
Doubling the recipe means multiplying the amount of each ingredient by 2. Therefore, you'll need (2 x 2/3) = 4/3 cups of sugar. This is equivalent to 1 and 1/3 cups.
Example 3: Discount Calculation
A store offers a 2/3 discount on an item. If the original price is $30, how much will you save?
The discount amount is (2/3) x $30 = $20. Therefore, you will save $20.
Frequently Asked Questions (FAQ)
-
Q: Is there a limit to the number of equivalent fractions for 2/3? A: No, there is an infinite number of equivalent fractions for 2/3, as you can multiply the numerator and denominator by any whole number greater than 1.
-
Q: How do I find the simplest form of a fraction? A: To find the simplest form, divide both the numerator and the denominator by their greatest common divisor (GCD).
-
Q: What if I multiply or divide the numerator and denominator by different numbers? A: If you multiply or divide the numerator and denominator by different numbers, you will change the value of the fraction and it will no longer be equivalent to the original fraction.
-
Q: Why is understanding equivalent fractions important? A: Understanding equivalent fractions is crucial for various mathematical operations, problem-solving, and applications in real-world scenarios as demonstrated throughout this article.
Conclusion: Mastering the Art of Equivalent Fractions
Understanding the concept of equivalent fractions, and specifically the numerous equivalents of 2/3, is a cornerstone of mathematical fluency. This article has explored various methods for finding these equivalents, highlighting the underlying mathematical principles, and demonstrating practical applications across various fields. By mastering the techniques presented here, you’ll gain a deeper understanding of fractions and their importance in everyday life and more advanced mathematical concepts. Remember that the key to working with equivalent fractions is always to maintain the ratio between the numerator and the denominator by multiplying or dividing both by the same non-zero number. Practice consistently, and you'll confidently navigate the world of fractions.
Latest Posts
Latest Posts
-
9 Divided By 1 3
Sep 16, 2025
-
6 5 8 As A Decimal
Sep 16, 2025
-
48 Hours Is How Long
Sep 16, 2025
-
7 5 As A Mixed Number
Sep 16, 2025
-
14 Percent As A Decimal
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Is Equivalent To What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.