9 Divided By 1 3
saludintensiva
Sep 16, 2025 · 5 min read
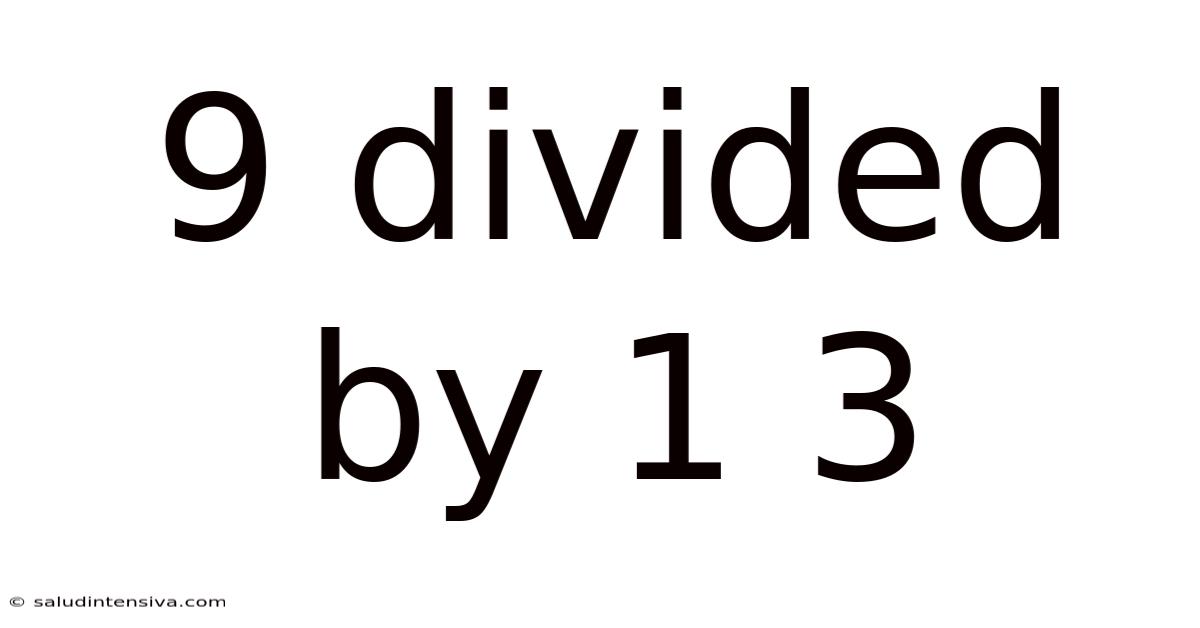
Table of Contents
Understanding 9 Divided by 1/3: A Comprehensive Guide
Dividing by fractions can seem daunting at first, but with a clear understanding of the underlying principles, it becomes a straightforward process. This article will comprehensively explore the problem of 9 divided by 1/3 (9 ÷ 1/3), breaking it down step-by-step, explaining the mathematical concepts involved, and providing practical examples to solidify your understanding. We'll move beyond simply providing the answer and delve into the why behind the calculation, making this a valuable resource for students and anyone looking to refresh their math skills.
Introduction: The Basics of Division
Before diving into the specifics of 9 ÷ 1/3, let's review the fundamental concept of division. Division essentially asks, "How many times does one number fit into another?" For example, 12 ÷ 3 asks, "How many times does 3 fit into 12?" The answer, of course, is 4.
When dealing with fractions, the concept remains the same, but the process requires a slightly different approach. We can't directly visualize fitting 1/3 into 9 in the same way we can visualize fitting 3 into 12. This is where understanding the reciprocal and the process of inverting and multiplying comes in.
Method 1: The Reciprocal Method
The most efficient way to divide by a fraction is to use the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/3 is 3/1 (or simply 3).
To divide by a fraction, we multiply by its reciprocal. Therefore, 9 ÷ 1/3 becomes:
9 × 3/1 = 9 × 3 = 27
Therefore, 9 divided by 1/3 equals 27.
This method simplifies the division problem into a much more manageable multiplication problem. It's crucial to understand why this works.
Method 2: Visual Representation
To further solidify this concept, let's consider a visual representation. Imagine you have 9 pies. If you want to divide these 9 pies into portions of 1/3 of a pie each, how many portions will you have?
Each pie can be divided into three 1/3 portions. Since you have 9 pies, you have 9 x 3 = 27 portions of 1/3 of a pie. This visual representation helps to understand the result intuitively.
Method 3: Understanding the Concept of "How Many Times Does it Fit?"
Let's revisit the question, "How many times does 1/3 fit into 9?" We can think of this in terms of repeated addition. How many times do we need to add 1/3 to itself to reach 9?
1/3 + 1/3 + 1/3 + ... = 9
This is equivalent to multiplying 1/3 by some number (let's call it 'x') to get 9:
(1/3) * x = 9
To solve for x, we can multiply both sides of the equation by 3 (the reciprocal of 1/3):
3 * (1/3) * x = 9 * 3
x = 27
This method reinforces the idea that dividing by a fraction is the same as multiplying by its reciprocal.
Explaining the Math Behind the Reciprocal Method
The reciprocal method isn't just a trick; it's grounded in solid mathematical principles. Let's explore the reasoning behind this method using the concept of multiplicative inverses.
Every non-zero number has a multiplicative inverse, also known as its reciprocal. The product of a number and its reciprocal is always 1. For example:
(1/3) * (3/1) = 1
Now consider the division problem 9 ÷ (1/3). We can rewrite this as a fraction:
9 / (1/3)
To simplify this complex fraction, we can multiply both the numerator and the denominator by the reciprocal of the denominator (3/1):
(9 * (3/1)) / ((1/3) * (3/1)) = (27/1) / 1 = 27
This demonstrates that multiplying by the reciprocal is a mathematically sound way to perform division with fractions.
Expanding the Concept: Dividing Other Numbers by Fractions
The principles we've discussed apply universally to dividing any number by a fraction. Let's consider a few examples:
- 15 ÷ 1/5: The reciprocal of 1/5 is 5. Therefore, 15 ÷ 1/5 = 15 × 5 = 75
- 2 ÷ 1/2: The reciprocal of 1/2 is 2. Therefore, 2 ÷ 1/2 = 2 × 2 = 4
- 7 ÷ 2/3: The reciprocal of 2/3 is 3/2. Therefore, 7 ÷ 2/3 = 7 × (3/2) = 21/2 = 10.5
Addressing Common Mistakes
A common mistake is to simply multiply the numerator and denominator directly without using the reciprocal. This yields an incorrect answer. Remember, division by a fraction requires multiplying by its reciprocal.
Another mistake is forgetting to convert mixed numbers into improper fractions before performing the division. For instance, if the problem was 9 ÷ 1 1/3, you would first convert 1 1/3 to the improper fraction 4/3, then proceed with the reciprocal method: 9 ÷ 4/3 = 9 × 3/4 = 27/4 = 6.75
Frequently Asked Questions (FAQ)
-
Q: Why do we multiply by the reciprocal when dividing by a fraction? A: This stems from the mathematical properties of multiplicative inverses and simplifying complex fractions. Multiplying by the reciprocal effectively eliminates the fraction from the denominator.
-
Q: Can I divide a fraction by a fraction using this method? A: Absolutely! For example, (1/2) ÷ (1/4) = (1/2) × (4/1) = 2
-
Q: What if I'm dividing by a whole number instead of a fraction? A: You can still think of the whole number as a fraction with a denominator of 1. For example, 9 ÷ 3 is the same as 9 ÷ 3/1 = 9 × 1/3 = 3
Conclusion: Mastering Fraction Division
Understanding the process of dividing by fractions is a crucial skill in mathematics. By grasping the concept of reciprocals and the underlying mathematical principles, you can confidently tackle division problems involving fractions, regardless of the complexity. Remember to practice regularly, using different methods to reinforce your understanding. This will not only improve your problem-solving skills but also build a stronger foundation for more advanced mathematical concepts. The key takeaway is to always remember to invert and multiply! With consistent practice and a focus on understanding the why behind the method, you'll master this essential mathematical operation.
Latest Posts
Latest Posts
-
Is 1 8 Bigger Than 3 16
Sep 16, 2025
-
Printable Military Time Conversion Chart
Sep 16, 2025
-
Half Of 1 2 Inch
Sep 16, 2025
-
Changing Decimals To Mixed Numbers
Sep 16, 2025
-
Adding Fractions Negative And Positive
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 9 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.