Is 1/8 Bigger Than 3/16
saludintensiva
Sep 16, 2025 · 5 min read
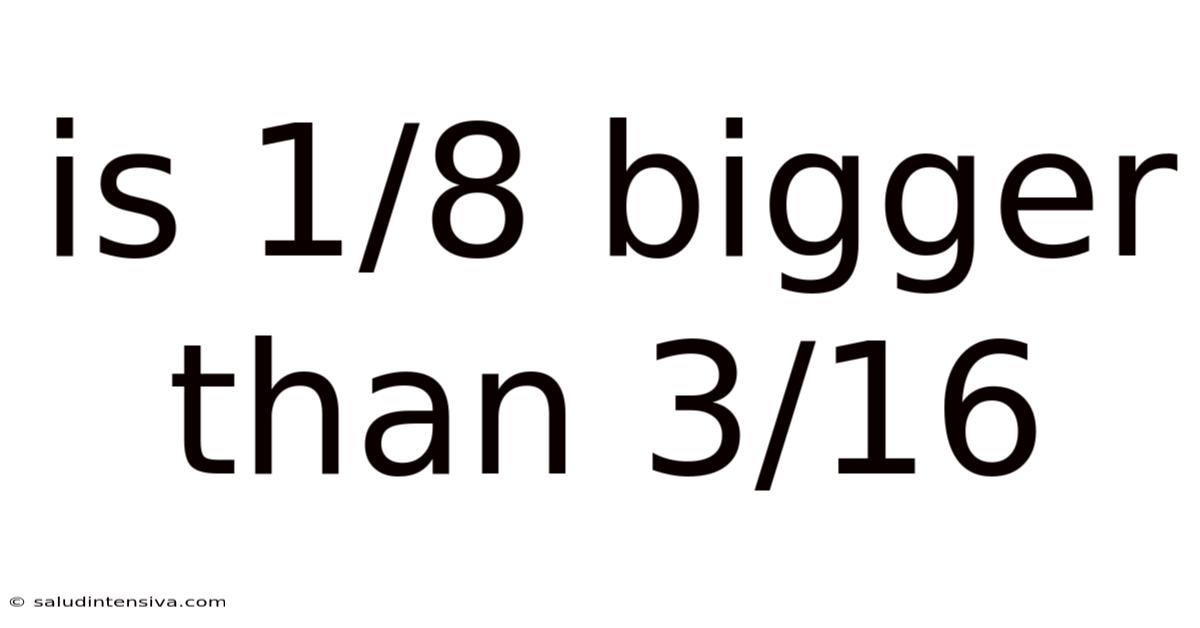
Table of Contents
Is 1/8 Bigger Than 3/16? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, essential for everyday life and advanced studies. This article will comprehensively explore the question: "Is 1/8 bigger than 3/16?" We'll delve into multiple methods for comparing fractions, explaining the concepts in a clear and accessible way, suitable for learners of all levels. By the end, you'll not only know the answer but also possess a solid understanding of fraction comparison techniques.
Introduction: Understanding Fractions
Before we tackle the specific comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 1/4, the whole is divided into 4 equal parts, and we are considering 1 of those parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This means converting both fractions so they have the same denominator. We can then easily compare the numerators.
Let's apply this to our problem: Is 1/8 bigger than 3/16?
- 1/8: The denominator is 8.
- 3/16: The denominator is 16.
The least common multiple (LCM) of 8 and 16 is 16. Therefore, we'll convert 1/8 to an equivalent fraction with a denominator of 16. To do this, we multiply both the numerator and the denominator of 1/8 by 2:
(1 x 2) / (8 x 2) = 2/16
Now we can compare:
- 2/16
- 3/16
Since 2 is smaller than 3, we can conclude that 2/16 is smaller than 3/16. Therefore, 1/8 is smaller than 3/16.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals. This allows for a direct numerical comparison.
To convert a fraction to a decimal, we divide the numerator by the denominator.
- 1/8: 1 ÷ 8 = 0.125
- 3/16: 3 ÷ 16 = 0.1875
Comparing the decimal values, we see that 0.125 is smaller than 0.1875. This confirms our previous finding: 1/8 is smaller than 3/16.
Method 3: Visual Representation
Visualizing fractions can be incredibly helpful, especially for beginners. Imagine a pizza cut into 8 equal slices (representing 1/8). Now imagine another pizza cut into 16 equal slices (representing 3/16). If you take 1 slice from the first pizza (1/8) and 3 slices from the second pizza (3/16), you'll visually see that the 3 slices from the second pizza represent a larger portion than the single slice from the first pizza. This visual comparison reinforces the conclusion that 1/8 is smaller than 3/16.
Method 4: Cross-Multiplication
Cross-multiplication is a quick technique for comparing two fractions. We multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. Then we compare the results.
Let's apply this to 1/8 and 3/16:
- 1 x 16 = 16
- 3 x 8 = 24
Since 16 < 24, we conclude that 1/8 < 3/16. Again, this demonstrates that 1/8 is smaller than 3/16.
Understanding the Relationship Between Numerators and Denominators
The apparent counter-intuitiveness of this result (a larger numerator, 3, resulting in a smaller fraction) stems from the crucial role of the denominator. The denominator dictates the size of each fractional part. A larger denominator means the whole is divided into more parts, and each individual part is smaller.
In this case, although 3 is larger than 1, the individual parts in 3/16 are significantly smaller than the individual parts in 1/8. This difference in the size of the fractional parts outweighs the difference in the number of parts being considered.
Practical Applications: Real-World Examples
Understanding fraction comparison is crucial in numerous real-world situations:
- Baking: Following recipes accurately requires understanding fraction equivalents and comparisons.
- Construction: Precise measurements in construction rely heavily on fractional understanding.
- Finance: Calculating percentages and proportions in financial contexts necessitates fraction manipulation.
- Data Analysis: Interpreting data presented in fractional or percentage forms requires proficiency in fraction comparison.
Frequently Asked Questions (FAQ)
Q: Are there other ways to compare fractions besides the methods discussed?
A: Yes, you can also use fraction calculators or visual aids like fraction bars or number lines to assist in comparing fractions. These tools can be particularly helpful for visualizing the relative sizes of fractions.
Q: What if I have more than two fractions to compare?
A: The same methods apply. Find a common denominator for all fractions or convert them all to decimals. Then, compare the numerators or decimal values to determine the order from smallest to largest.
Q: How can I improve my understanding of fractions?
A: Practice is key. Work through various exercises, using different methods to compare fractions. Visual aids, real-world examples, and interactive online tools can also significantly enhance understanding.
Q: Why is it important to learn about fractions?
A: Fractions are the building blocks of many mathematical concepts. A solid understanding of fractions is essential for mastering more advanced mathematical topics, such as algebra, geometry, and calculus. Furthermore, it is essential for numerous practical applications in daily life.
Conclusion: Mastering Fraction Comparison
Comparing fractions may seem daunting at first, but with consistent practice and a clear understanding of the underlying concepts, it becomes a simple and intuitive process. We've explored four different methods for comparing fractions – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – each offering a unique approach to solving the problem. Remember, the key is to understand that the denominator plays a vital role in determining the size of the fractional part. By mastering these techniques, you'll be well-equipped to confidently tackle fraction comparisons in any context. Remember that 1/8 is definitively smaller than 3/16. Understanding why is the key to true mathematical literacy.
Latest Posts
Latest Posts
-
44 Degrees F To C
Sep 16, 2025
-
1 2 1 5 In Fraction
Sep 16, 2025
-
19 Years Ago From Today
Sep 16, 2025
-
What Is 80 Of 10
Sep 16, 2025
-
Is 3 4 More Than 2 3
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 1/8 Bigger Than 3/16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.